В этом году первый набор Факультета Компьютерных Наук заканчивает третий курс, у них прошел первый год специализаций (предыдущие посты про новости ФКН: 1, 2, 3, 4, 5).
Все студенты 3-го года обучения прошли курс по машинному обучению от Евгения Соколова (автора известной специализации на Coursera и руководителя отдела машинного обучения сервиса Яндекс.Дзен). Если вы еще учитесь в школе, то вы можете послушать Евгения в летней школе ФКН; также он отвечает за преподавание машинного обучения в августовской параллели A-ML ЛКШ.
Также общим был курс методов оптимизации, состоявший из непрерывной части и курса по комбинаторной оптимизации от Максима Бабенко, руководителя отдела технологий распределенных вычислений в Яндексе, в прошлом вице-чемпиона ACM ICPC. Среди семинаристов курса также хорошо известный вам Zlobober.
Студенты 3-го курса учились на специализациях машинное обучение, распределенные системы, анализ данных и интеллектуальные системы, анализ и принятие решений. В этом году второкурсники также смогли выбрать специализацию по теоретической информатике.
Радует, что уровень поступающих к нам каждый год растёт. Это ясно и из отзывов преподавателей, и из результатов поступивших к нам абитуриентов на школьных олимпиадах. Каждый год мы заметно повышаем требования для поступления по олимпиадам, и несмотря на это, каждый год у нас происходит перенабор из-за поступающих олимпиадников. Кстати, у нас ежегодно проходят встречи в Яндексе с победителями всероссийских олимпиад, и вот видео последних двух встреч: 1, 2.










 . Иначе рассмотрим, какой ожидаемый вклад в изменение настроения даст
. Иначе рассмотрим, какой ожидаемый вклад в изменение настроения даст 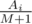 . Для невкусных конфет ожидаемый вклад в изменение настроения равен
. Для невкусных конфет ожидаемый вклад в изменение настроения равен 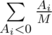 , так как первой невкусной конфетой может оказаться равновероятно любая из невкусных. В итоге математическое ожидание изменения настроения равно
, так как первой невкусной конфетой может оказаться равновероятно любая из невкусных. В итоге математическое ожидание изменения настроения равно 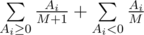 .
.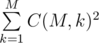 .
.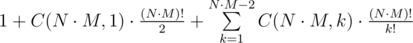 .
.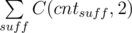 , где суммирование ведётся по всем суффиксам.
, где суммирование ведётся по всем суффиксам.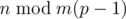 — хорошее. Рассчитаем и запомним в таблице для каждого
— хорошее. Рассчитаем и запомним в таблице для каждого 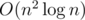 .
.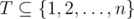 ассистентом и выполняет остальные задачи сам (но необязательно в последовательные дни), то существует оптимальное расписание, в котором профессор передает задачи из подмножества
ассистентом и выполняет остальные задачи сам (но необязательно в последовательные дни), то существует оптимальное расписание, в котором профессор передает задачи из подмножества 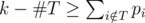 .
.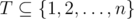 за дни после
за дни после 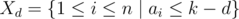 — множество задач, которые могут быть переданы в день
— множество задач, которые могут быть переданы в день 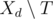 непусто, то мы можем в день
непусто, то мы можем в день 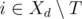 , которая максимизирует значение
, которая максимизирует значение 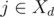 (так как ассистент выполнит задачу в срок) и
(так как ассистент выполнит задачу в срок) и 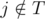 (мы предполагаем, что расписание
(мы предполагаем, что расписание 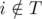 и
и 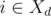 ). Иначе, если
). Иначе, если 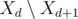 в кучу (то есть задачи с
в кучу (то есть задачи с  .
.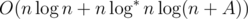 .
. для обозначения получающихся частей. Решение этой задачи получается в три шага.
для обозначения получающихся частей. Решение этой задачи получается в три шага.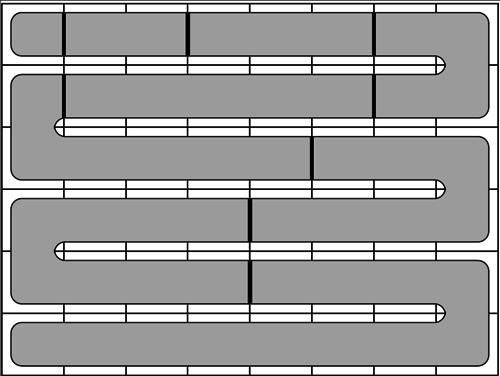

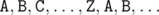 в том порядке, в котором части появляются на змейке. Однако в некоторых случаях такой способ не работает.
в том порядке, в котором части появляются на змейке. Однако в некоторых случаях такой способ не работает. . Пусть
. Пусть 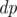 , где
, где 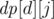 — истина если и только если делитель
— истина если и только если делитель 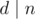 :
: 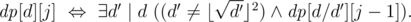
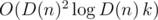 (логарифм появляется из-за использования структуры map или аналогичной для хранения делителей
(логарифм появляется из-за использования структуры map или аналогичной для хранения делителей 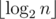 , что в нашем случае не более 29. Действительно, для
, что в нашем случае не более 29. Действительно, для 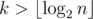 ответ всегда «NO» (доказательство следует из следующего решения).
ответ всегда «NO» (доказательство следует из следующего решения).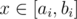 тогда и только тогда, когда возможно добиться того, чтобы на
тогда и только тогда, когда возможно добиться того, чтобы на 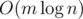 .
.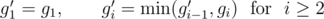
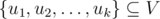 представлять собой одну или более связных компонент графа в данный момент времени.
представлять собой одну или более связных компонент графа в данный момент времени.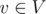 мы храним в ячейке массива
мы храним в ячейке массива 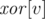 результат операции
результат операции 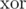 , примененной к весам всех ребер, инцидентных этой вершине. Заметим, что такие значения можно обновлять за время
, примененной к весам всех ребер, инцидентных этой вершине. Заметим, что такие значения можно обновлять за время 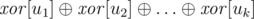
 обозначает операцию
обозначает операцию 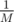 , где
, где  такое же число, но при этом разрешим стикерам выходить за границу и накрывать позиции из
такое же число, но при этом разрешим стикерам выходить за границу и накрывать позиции из  стикеров.
стикеров.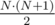 .
. . Существует быстрый способ посчитать
. Существует быстрый способ посчитать 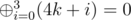 . Значит,
. Значит, 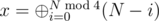 .
. . Значит, чтобы из кучки
. Значит, чтобы из кучки 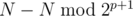 , их ровно половина. Если в
, их ровно половина. Если в 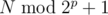 .
.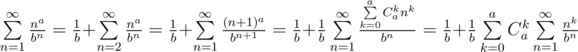
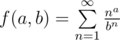 , имеем
, имеем 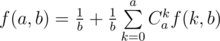
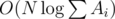 . Также следует учесть, что нужно предварительно отсортировать темы по значению
. Также следует учесть, что нужно предварительно отсортировать темы по значению 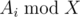 для поиска тем с максимальным количеством задач, когда у Гены уже нет возможности решать по
для поиска тем с максимальным количеством задач, когда у Гены уже нет возможности решать по 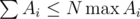 , и свойств логарифма, получается
, и свойств логарифма, получается 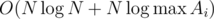 .
.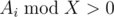 .
.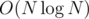 .
.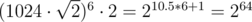 , и вычисления можно производить в беззнаковых 64-битных целых. При этом при сравнении дробей потребуется или использовать встроенные типы для работы с длинными числами (в тех языках, в которых они есть), либо использовать модулярную арифметику, либо вычислять НОД, либо хранить старшую часть числа отдельно...
, и вычисления можно производить в беззнаковых 64-битных целых. При этом при сравнении дробей потребуется или использовать встроенные типы для работы с длинными числами (в тех языках, в которых они есть), либо использовать модулярную арифметику, либо вычислять НОД, либо хранить старшую часть числа отдельно...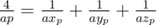 . Таким образом, достаточно сначала предпросчётом построить таблицу для всех простых чисел и для
. Таким образом, достаточно сначала предпросчётом построить таблицу для всех простых чисел и для 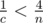 , то
, то 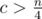 . Так как
. Так как 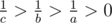 , а значит
, а значит 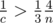 , тем самым
, тем самым 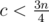 ; из аналогичных соображений
; из аналогичных соображений 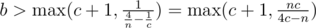 и
и 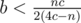 . Соответственно, перебираем для всех простых
. Соответственно, перебираем для всех простых 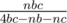 . При этом размер кода не будет превосходить 50k, что меньше, чем source limit.
. При этом размер кода не будет превосходить 50k, что меньше, чем source limit. в сумму двух «египетских» дробей, использовав алгоритм Фибоначчи; в этом случае решение укладывается в Time Limit без предрасчёта (именно такие решения и сдали оба участника, решивших задачу).
в сумму двух «египетских» дробей, использовав алгоритм Фибоначчи; в этом случае решение укладывается в Time Limit без предрасчёта (именно такие решения и сдали оба участника, решивших задачу).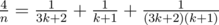 ,
,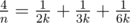 ,
,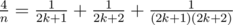 ,
,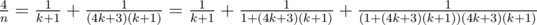 ,
,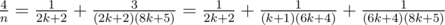 .
.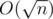 . Можно также изначально разложить число
. Можно также изначально разложить число 








