My code for Enumerate Palindromes passes all the cases.
But it has a fatal bug and should tle.
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | Qingyu | 153 |
| 7 | djm03178 | 152 |
| 7 | adamant | 152 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
My code for Enumerate Palindromes passes all the cases.
But it has a fatal bug and should tle.
r = i + res[i];
b = i;
if (i + res[i] > r) {
r = i + res[i];
b = i;
}
ll n = 1e5;
string s = "";
for (ll i = 0; i < n; i++) {
s += 'j';
s += 'k';
}
cout << s <<"\n";
Given a tree with $$$N$$$ vertices, find the number of rooted trees (which consist of some edges present in the given tree) with $$$K$$$ vertices, including vertex 1. Constraints: $$$1 \leq K \leq N \leq 3000$$$.
Example :
Let $$$N$$$ = $$$5$$$ and the tree be this :
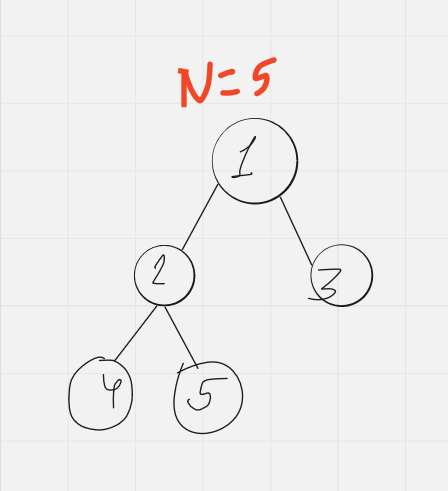
Then for K = 1, 2, 3, 4, 5 the solutions are :
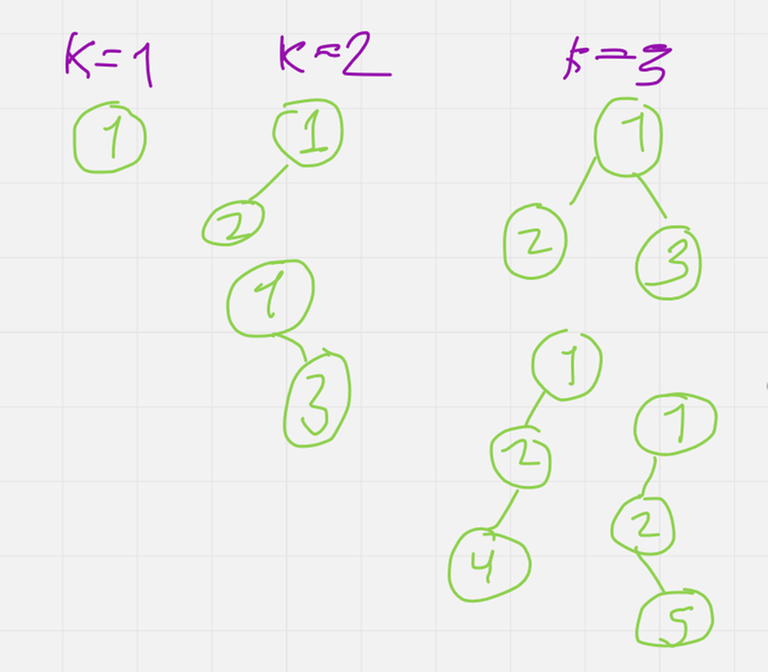
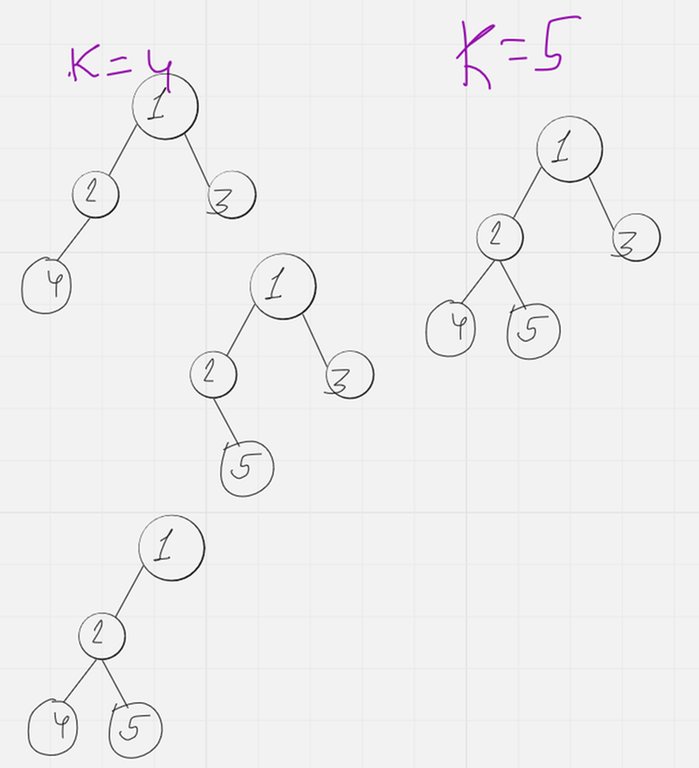
I found a tutorial but it is in Japanese, do you know some good English tutorials.
I wanted to ask why my solution for this problem works!
Logic lies inside the solve function.
238096776
First, I find the intervals which can be just turned on by just 1 bulb, and then for each interval, I find number of bulbs that can single handedly turn on the whole interval.
To do this i consider this bulb and it counterpart bulb (which also lies in this interval), then i query in the range formed by the two bulbs the min value and max value of oth (using segment tree), and then expand my range to the new indices.
If range becomes equal to total interval size then we lit up whole range, else if range size did not increase and whole interval is not covered then we can not cover this whole range so we skip this blub.
I am not sure why this works fast.
for each bulb i store the index of it counterpart in oth array.
Sombody help me with time complexity.
Past week, i was asked this problem in an interview, i don't know the solution till now, help me with this.
There are $$$N$$$ people in a group, weight of $$$i$$$ 'th person is $$$W[i]$$$, there is a lift of capacity $$$C$$$ which is the maximum weight the lift can carry, everyone wants to go to the top floor via lift.
Determine $$$M$$$, where $$$M$$$ is the minimum times lift must be used by the group so that everyone is able to go to the top floor.
Not sure about constraints, please give the best solution you can.
$$$N$$$ = 4
$$$C$$$ = 90
$$$W$$$ = [10, 20, 70, 80]
$$$ANS$$$ = 2
Five men and nine women stand equally spaced around a circle in random order. The probability that every man stands diametrically opposite a woman is $$$\frac{m}{n},$$$ where $$$m$$$ and $$$n$$$ are relatively prime positive integers. Find $$$m+n.$$$
191
Total Ways = $$$\binom{14}{5}$$$. Out of $$$14$$$ places choose $$$5$$$ places for men. Women will follow.
There are total $$$7$$$ pairs of seats. Choose $$$5$$$ out of them. For each pair of seats there are $$$2$$$ ways.
So required ways = $$$\binom{7}{5} \cdot 2^5$$$
Required Probability = $$$\frac{\binom{7}{5} \cdot 2^5}{\binom{14}{5}}= \frac{48}{143}$$$.
A plane contains $$$40$$$ lines, no $$$2$$$ of which are parallel. Suppose there are $$$3$$$ points where exactly $$$3$$$ lines intersect, $$$4$$$ points where exactly $$$4$$$ lines intersect, $$$5$$$ points where exactly $$$5$$$ lines intersect, $$$6$$$ points where exactly $$$6$$$ lines intersect, and no points where more than $$$6$$$ lines intersect. Find the number of points where exactly $$$2$$$ lines intersect.
607
Two lines can only intersect once.
Maximum number of intersections = $$$\binom{n}{2}$$$ (Choose any two lines and they intersect)
Maximum number of intersections occur when for each intersection point there are only two lines intersecting at that point. Lets label these $$$T2$$$ intersection points.
If there are intersection points where there are $$$x$$$ ($$$x$$$ > $$$2$$$) lines intersecting at some point, then we will lose $$$T2$$$ points.
Amount of point we lost = Amount of points $$$x$$$ lines could have contributed = $$$\binom{x}{2}$$$
So the final answer becomes
$$$\binom{40}{2} - 3\binom{3}{2} - 4\binom{4}{2}- 5\binom{5}{2}- 6\binom{6}{2} = \boxed{607}.$$$
The sum of all positive integers $$$m$$$ for which $$$\tfrac{13!}{m}$$$ is a perfect square can be written as $$$2^{a}3^{b}5^{c}7^{d}11^{e}13^{f}$$$, where $$$a, b, c, d, e,$$$ and $$$f$$$ are positive integers. Find $$$a+b+c+d+e+f$$$.
12
Power of $$$x$$$ in $$$n!$$$ = $$$\lfloor \frac{n}{x} \rfloor + \lfloor \frac{n}{x^{2}} \rfloor+ \lfloor \frac{n}{x^3{}} \rfloor + ...$$$ Using this formula we get.. $$$13! = 2^{10} \cdot 3^{5} \cdot 5^{2} \cdot 7^{1} \cdot 11^{1} \cdot 13^{1}$$$
For a number to be perfect square it prime factorisation should consist of even powers.
Let's write it even and odd powers seperately $$$13! = 2^{10} \cdot 3^{4} \cdot 5^{2} \cdot 3^{1} \cdot 7^{1} \cdot 11^{1} \cdot 13^{1}$$$
Now we want sum of all numbers $$$2^{x} \cdot 3^{y} \cdot 5^{z} \cdot 3^{1} \cdot 7^{1} \cdot 11^{1} \cdot 13^{1}$$$
such that $$$0 \leq x \leq 10 $$$ and $$$0 \leq y \leq 4$$$ and $$$0 \leq z \leq 2$$$ and $$$x, y, z$$$ are even
The resultant number will be $$$\sum\limits_{x} \sum\limits_{y} \sum\limits_{z}2^{x} \cdot 3^{y} \cdot 5^{z} \cdot 3^{1} \cdot 7^{1} \cdot 11^{1} \cdot 13^{1}$$$
which is
$$$(\sum\limits_{x} (2^{x}))\cdot (\sum\limits_{y} (3^{y})) \cdot (\sum\limits_{z} (5^{z})) \cdot 3^{1} \cdot 7^{1} \cdot 11^{1} \cdot 13^{1}$$$
This can be computed using GP series.
final answer = $$$ 2^{1} \cdot 3^{2} \cdot 5^{1} \cdot 7^{3} \cdot 11^{1} \cdot 13^{4}$$$
There exists a unique positive integer $$$a$$$ for which the sum $$$[U=\sum_{n=1}^{2023}\left\lfloor\dfrac{n^{2}-na}{5}\right\rfloor]$$$ is an integer strictly between $$$-1000$$$ and $$$1000$$$. For that unique $$$a$$$, find $$$a+U$$$.
(Note that $$$\lfloor x\rfloor$$$ denotes the greatest integer that is less than or equal to $$$x$$$.)
944
Consider an $$$n$$$-by-$$$n$$$ board of unit squares for some odd positive integer $$$n$$$. We say that a collection $$$C$$$ of identical dominoes is a maximal grid-aligned configuration on the board if $$$C$$$ consists of $$$(n^2-1)/2$$$ dominoes where each domino covers exactly two neighboring squares and the dominoes don't overlap: $$$C$$$ then covers all but one square on the board. We are allowed to slide (but not rotate) a domino on the board to cover the uncovered square, resulting in a new maximal grid-aligned configuration with another square uncovered. Let $$$k(C)$$$ be the number of distinct maximal grid-aligned configurations obtainable from $$$C$$$ by repeatedly sliding dominoes. Find the maximum value of $$$k(C)$$$ as a function of $$$n$$$.
$$$\frac{(n+1)^{2}}{4}$$$ , The Optimal Solution would be a spiral (first along the boundaries then curled inside).
2023 AIME and 2023 USAJMO
Math problems that aim to aid competitive programming skills.
Target audience : Experts and below.
we have a permutation p of size N.
we iterate on this permutation and insert elements into a Binary Search Tree.
Prove that each sub-tree will consists of all elements from some l to r.
In other words, prove that elements of each sub-tree form continuous subarray of identity permutation (if written is sorted order).
identity permutation -> 1, 2, 3, 4 ... N.
You are give a permutation of length n. Among all rotations of this permutation find out the one with maximum number of cycles.
Cycles here mean that cyles in the graph of permutation which contains edges from element->corresponding index. (One based indexing)
n <= 3e5
UPD : Solved
- Observe that it will be most optimal when both the travellers start at same position and move in opposite direction.
Proof:
In general case, the travellers will pass each other twice.
At the time of first meet it will be like this -> One of the travellers is waiting at rest area for other to pass, as other passes it they will meet again for second meet afterwards. So it is better if they started at the same meet point in different directions, answer would always be less. Hence proved. (Because the first meet point has become the start so does not add anything to the wait time, so it is better.)
- Now we just have to solve if they had to start at rest point A[i]. To solve this note that their meeting point will be L-A[i]. - It will lie between two rest positions (may coincide also) such that A[j] <= L-A[i] <= A[k], min waiting time will be ..
- 2 * ( min ( (L-A[i]-A[j]) , A[k]-(L-A[i])) ).
- To get final answer, Add the min waiting time to 2*L.
Most of the number theory problems involving divisors etc that have intended solutions using mobious or inclusion exclusions (I-E), do not really need these buzzwords, there is almost always an easier solution using dp. We can still say its I-E, but code is sort.
Let's calculate dp[i] where dp[i] denotes no of segments which have gcd(min, max) = i. To calculate dp[i], we can first calculate the no of segments which have gcd as multiple i, this part is easy and the same as editorial.
Then subtract dp[k*i] from dp[i] where 2<=k<=n/i. These will remove all segments which have gcd multiple of i but no exactly i. At last just print dp[1].
I forgot to mention one should find these dp values in descending order.
These comments were taken from
aryanc403 's twitter.
Problem in discussion is: AtCoder ABC304 F Shift table
Today i tried topcoder and the experience was just horrible.
First it was hard to figure out how/where to submit etc., not at all intuitive or beginner friendly
Couldn't submit my solution, "COPY BYTE error.." something like that.
Even vjudge could not submit.
Tried to download the arena applet, for that i didn't have the password, so tried creating new account but the one time verification email won't come.
The starting experience was just horrible.
You are given positive integers N and L. Count all sequences of positive integers with the following properties:
- The sequence is strictly increasing.
- The length of the sequence is L.
- No two consecutive elements share the same parity.
Return the number of these sequences, modulo 1e9 + 7.
N <= 1e5 and L <= N.
elements in sequence can be from 1 to N.
I broke it into two parts.
- Part 1 : o e o e o e ...
- Part 2 : e o e o e o ...
I have thought of dp.
Then Lets solve for o e o e .., second part will be similar.
dp[i][j] : Number of ways to fill upto index i such that number at index i is j. If i is odd then j must be odd.
dp[i][j] = dp[i-2][j-2] * 1 + dp[i-2][j-4] * 2 + dp[i-2][j-6] * 3 ... -- eq1
This is O(N*N*N) Solution.
dp[i][j-2] = dp[i-2][j-4] * 1 + dp[i-2][j-6] * 2 + dp[i-1][j-8] * 3 ... --eq2
Then eq1 - eq2 gives me,
dp[i][j] = dp[i][j-2] + dp[i-2][j-2] + dp[i-2][j-4] + dp[i-2][j-6] + dp[i-2][j-8] ...
this can now be done in O(N*N), but will surely give TLE in above constraints.
So how to proceed further?
Are there any optimization / tricks in this dp.
Or I should think something else which is not dp.
Don't wanna know the solution, just tell if there is some general concept/trick that i need to know, or i just need to think more on it.
Thanks.
You are given two vectors A and B, for each 1 <= k <= 2*N we want to find out C[k] where C[k] is sum of all A[i]*B[j] such that i + j == k.
N <= 1e6
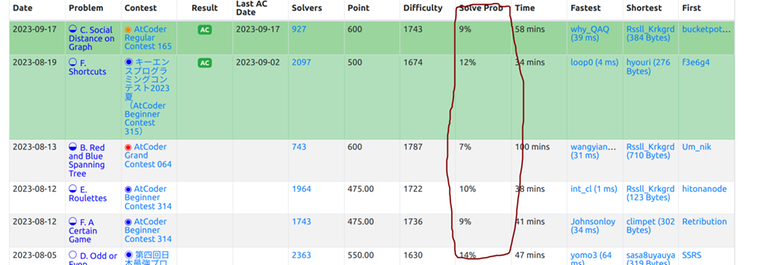
I was wondering how solve probability in kenkooo is claculated.
You are given a vector of pairs (x_i, y_i) for size N.
Constraint : 1 <= x_i,y_i <=N and N<=1e5
For each j from 1 to N, find out the maximum value of j*x_i + y_i amongst all i's from 1 to N.
Finally print those N values.
I, recenty started doing atcoder problems, I am able to make codeforces rated 2100 in 3 — 4 hours, 1900 in 2 — 3 hours but even atcoder(kenkoooo) problem rated 1250, 1300 feel hard. Does any one have similar experiences? Or it is just me :(
| Name |
|---|


