Except hints/solutions, I try to add a "general idea" section discuss about some general strategy and standard ideas used to solve the problem, hope you would like it :)
idea & solution: Misuki
What's the most obvious lower bound of the answer?
Is the lower bound achievable?
One standard way to solve optimization problem is to make observation on lower(upper) bound of the answer and prove such bound is achievable, it's useful in lot of problems.
Let $$$x$$$ be one of the most frequent elements in $$$a$$$, then the answer must be at least $$$(n - \text{frequency of } x)$$$, and this lower bound is always achievable by keep erasing a non-$$$x$$$ element from $$$a$$$, and we can prove it's always possible to do so.
proof:
If all elements of $$$a$$$ are $$$x$$$, we are done. Otherwise, let $$$y$$$ denote all the elements that are not $$$x$$$, then $$$a$$$ would have some subarray of the form $$$x \ldots x, y \ldots y, x \ldots x$$$. In this subarray, there must exist adjacent elements that satisfy $$$a_i \leq a_{(i \bmod m) + 1}$$$, otherwise we would have $$$x > y > \ldots > y > x$$$ implying $$$x > x$$$ which leads to a contradiction.
#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
int main() {
ios::sync_with_stdio(false), cin.tie(NULL);
int t; cin >> t;
while(t--) {
int n; cin >> n;
vector<int> a(n);
for(int &x : a) cin >> x;
vector<int> freq(n + 1);
for(int x : a) freq[x]++;
cout << n - (*max_element(freq.begin(), freq.end())) << '\n';
}
}
idea & solution: Misuki
Write a few small cases (ex. $$$n = 3, 4, 5$$$) and play with it, can you notice something interesting about the cost function?
Write a few examples and play with it is a good start to solve ad-hoc problems.
Consider subtask — decision version of the problem (i.e. yes/no problem) as follow: "Given a fixed $$$p$$$, check if this permutation is valid."
The above problem would reduce to finding minimum number of carriage return operations needed for each typewriter.
Now you know how to solve above problem, do you notice something interesting about the cost function?
In lot of problems, decision version of the problem is usually a useful subtask to consider.
Consider the cost function:
Let $$$c_1, c_2$$$ denote the minimum number of carriage return operations needed to make $$$a = p$$$ if Misuki is using first/second typewritter. Let's consider how to calculate them.
For $$$c_1$$$, we need to do carriage return operation whenever the position of value $$$x + 1$$$ is before $$$x$$$, for all $$$x \in [1, n - 1]$$$, so $$$c_1 = (\text{#}x \in [1, n - 1] \text{ such that } \mathrm{pos}_x > \mathrm{pos}_{x + 1})$$$.
Similarly, $$$c_2 = (\text{#}x \in [1, n - 1] \text{ such that } \mathrm{pos}_x < \mathrm{pos}_{x + 1})$$$.
Since for $$$x \in [1, n - 1]$$$, either $$$\mathrm{pos}_x < \mathrm{pos}_{x + 1}$$$ or $$$\mathrm{pos}_x > \mathrm{pos}_{x + 1}$$$ would hold, so we have $$$c_1 + c_2 = n - 1$$$, which is a constant, and $$$c_1 = c_2 \leftrightarrow c_1 = \frac{n - 1}{2}$$$, which only has solution when $$$n$$$ is odd, and such $$$p$$$ can be constructed easily (for example, $$${n - 1, n, n - 3, n - 2, ..., 4, 5, 2, 3, 1}$$$).
#include <iostream>
#include <numeric>
#include <vector>
using namespace std;
int main() {
ios::sync_with_stdio(false), cin.tie(NULL);
int t; cin >> t;
while(t--) {
int n; cin >> n;
if (n % 2 == 0) {
cout << -1 << '\n';
} else {
vector<int> p(n);
iota(p.begin(), p.end(), 1);
for(int i = 1; i < n; i += 2)
swap(p[i], p[i + 1]);
for(int i = 0; i < n; i++)
cout << p[i] << " \n"[i + 1 == n];
}
}
}
idea: feecle6418, solution: Kaey
Imagine we have $$$n$$$ isolated vertices initially, can you find any edge connect two component using reasonable number of queries?
Use binary search.
It's easy to verify that querying $$$a$$$ and $$$b$$$ will return the midpoint of the path between $$$a$$$ and $$$b$$$. In case the path has odd length, the node closer to $$$a$$$ of the two central nodes will be returned.
We will now construct the tree by expanding a connected component. Let $$$A = \{1\}$$$ and $$$B = \{2,\ldots,n\}$$$. While $$$B$$$ is not empty, choose any $$$b \in B$$$ and $$$a \in A$$$. Let $$$P$$$ be the path between $$$a$$$ and $$$b$$$. By construction, $$$P$$$ will consist of a prefix contained in $$$A$$$ and a suffix contained in $$$B$$$. We can binary search for the first $$$i$$$ such that $$$P_i \in B$$$.
This will take at most $$$\lceil log(|P|) \rceil + 2$$$ queries. Then, $$$(P_{i-1}, P_i)$$$ will be an edge of the tree, so we will set $$$A = A \cup {P_i}$$$ and $$$B = B \backslash {P_i}$$$.
The total number of queries will be smaller than $$$n \lceil log(n) \rceil + 2n = 12000$$$.
Consider we have $$$n$$$ isolated vertices initially, and try to keep finding an edge connect two different component.
Assume $$$u, v$$$ is at different component, then we have the following possible cases for the answer $$$x$$$.
- $$$x = u$$$: which means $$$u, v$$$ are connected by an edge and we are done.
- $$$x$$$ belongs to same component of $$$u$$$, seting $$$u := x$$$.
- $$$x$$$ belongs to same component of $$$v$$$, seting $$$v := x$$$.
- $$$x$$$ belongs to other component than $$$u, v$$$, in such case, either setting $$$u := x$$$ or $$$v := x$$$.
in case 1. we are done, and in case 2, 3, 4, we shorten the distance between $$$u, v$$$ by about half while keeping them not belongs to same component, so we can find an edge connect two component in $$$O(\lg n)$$$ queries and we are done.
#include <iostream>
#include <system_error>
#include <vector>
using namespace std;
int qry(int a, int b){
cout << "? " << a+1 << ' ' << b+1 << endl;
fflush(stdout);
int r; cin >> r;
return r-1;
}
void solve(){
int N; cin >> N;
vector<int> in_tree(N, 0), stk;
for (size_t i = 1; i < N; ++i)
stk.push_back(i);
in_tree[0] = 1;
vector<pair<int, int>> edges;
while(!stk.empty()){
int n = stk.back();
stk.pop_back();
if(in_tree[n])continue;
int l = 0, r = n;
while(1){
int q = qry(l, r);
if(q == l){
in_tree[r] = 1;
edges.push_back({l, r});
break;
}
if(in_tree[q])l = q;
else r = q;
}
stk.push_back(n);
}
cout << "! ";
for(auto [x, y]: edges)cout << x+1 << ' ' << y+1 << ' ';
cout << endl;
}
int main(){
int t; cin >> t;
while(t--)solve();
}
#include <iostream>
#include <numeric>
#include <vector>
#include <array>
using namespace std;
int query(int u, int v) {
cout << "? " << u + 1 << ' ' << v + 1 << '\n';
int x; cin >> x;
return x - 1;
}
int main() {
int t; cin >> t;
while(t--) {
int n; cin >> n;
vector<array<int, 2>> e;
vector<int> c(n);
iota(c.begin(), c.end(), 0);
auto addEdge = [&](int u, int v) {
e.push_back({u, v});
vector<int> cand;
for(int i = 0; i < n; i++)
if (c[i] == c[v])
cand.emplace_back(i);
for(int i : cand)
c[i] = c[u];
};
for(int i = 0; i < n - 1; i++) {
int u = 0, v = 0;
while(c[v] == c[u]) v++;
int x;
while((x = query(u, v)) != u) {
if (c[u] == c[x]) u = x;
else v = x;
}
addEdge(u, v);
}
cout << "!";
for(auto [u, v] : e) cout << ' ' << u + 1 << ' ' << v + 1;
cout << '\n';
}
}
2001D - Longest Max Min Subsequence
idea & solution: Misuki, tester's code: SorahISA
Forget about minimize lexicographical order. What's the size of longest $$$b$$$ we can get?
It's the number of different elements. Try to minimize/maximize first element in $$$b$$$ without reducing the max size of $$$b$$$ we can get.
When solving problem asking for minimize/maximize lexicographical order of something, we can often construct them by minimize/maximize first element greedily.
Consider subtask:
Let's ignore the constraint where $$$b$$$ should be lexicographically smallest. How can we find the length of $$$b$$$?
Apparently, it is the number of distinct elements in $$$a$$$. Let's call it $$$k$$$.
Construct $$$b$$$ from left to right without worsening the answer:
Now we know how to find the maximum possible length of $$$b$$$. Let's try to construct $$$b$$$ from left to right without worsening the answer, and greedily minimize its lexicographical order. Assume we pick $$$a_i$$$ as the $$$j$$$-th element in $$$b$$$, then there should be $$$k - j$$$ distinct elements in the subarray $$$a[i + 1, n]$$$ after deleting all elements that appear in the subarray $$$b[1, j]$$$.
Assume we already construct $$$b_1, b_2, \ldots, b_j$$$ where $$$b_j = a_i$$$ and we want to find $$$b_{j + 1}$$$, and let $$$l_x$$$ be the last position where $$$x$$$ occurs in the subarray $$$a[i + 1, n]$$$ or $$$\infty$$$ if it doesn't exist, then we can choose anything in $$$a[i + 1, \min\limits_{1 \le x \le n}(l_x)]$$$. And to minimize lexicographical order, we need to choose the maximum element in it if $$$(j + 1)$$$ is odd, or the minimum element otherwise. If there are multiple of them, choose the leftmost one of them is optimal since we would have a longer suffix of $$$a$$$ for future construction.
Then observe for the candidate window (i.e. $$$a[i + 1, \min\limits_{1 \le x \le n}(l_x)]$$$), its left bound and right bound are non-decreasing, so we can use priority queues or set to maintain all possible candidates by storing $$$(a_{pos}, pos)$$$, and another priority queue or set to maintain all $$$l_x > i$$$. And the total time complexity is $$$O(nlgn)$$$.
#include <iostream>
#include <vector>
#include <queue>
#include <array>
#include <climits>
using namespace std;
int main() {
ios::sync_with_stdio(false), cin.tie(0);
int t; cin >> t;
while(t--) {
int n; cin >> n;
vector<int> a(n);
for(int &x : a) {
cin >> x;
x--;
}
vector l(n + 1, INT_MAX);
for(int i = 0; i < n; i++)
l[a[i]] = i;
priority_queue<int, vector<int>, greater<int>> ls(l.begin(), l.end());
priority_queue<array<int, 2>, vector<array<int, 2>>, greater<array<int, 2>>> mx_cand, mn_cand;
vector<bool> used(n, false);
for(int i = 0; i <= ls.top(); i++) {
mx_cand.push({-a[i], i});
mn_cand.push({a[i], i});
}
vector<int> b;
int i = 0;
while(!mn_cand.empty()) {
auto [x, pos] = (b.size() % 2 == 0 ? mx_cand.top() : mn_cand.top());
if (b.size() % 2 == 0) {
mx_cand.pop();
x *= -1;
} else {
mn_cand.pop();
}
b.emplace_back(x);
i = pos + 1, used[x] = true;
while(ls.top() != INT_MAX and used[a[ls.top()]]) {
int j = ls.top(); ls.pop();
for(int k = j + 1; k <= min(ls.top(), n - 1); k++) {
mx_cand.push({-a[k], k});
mn_cand.push({a[k], k});
}
}
while(!mx_cand.empty() and (used[-mx_cand.top()[0]] or mx_cand.top()[1] < i)) mx_cand.pop();
while(!mn_cand.empty() and (used[mn_cand.top()[0]] or mn_cand.top()[1] < i)) mn_cand.pop();
}
cout << b.size() << '\n';
for(int i = 0; i < b.size(); i++)
cout << b[i] + 1 << " \n"[i + 1 == b.size()];
}
}
#include <cstdint>
#include <iostream>
#include <set>
#include <vector>
using namespace std;
void solve() {
int N; cin >> N;
vector<int> A(N);
for (int &x : A) cin >> x, --x;
vector<int> cnt(N, 0), is_last(N, 0), last_pos(N, -1);
for (int i = N-1; i >= 0; --i) {
if (!cnt[A[i]]++) is_last[i] = 1, last_pos[A[i]] = i;
}
vector<int> ans;
multiset<int> st;
int l = 0, r = -1, flag = 0;
while (r+1 < N) {
while (r+1 < N and (r == -1 or !is_last[r])) {
++r;
if (is_last[last_pos[A[r]]]) st.emplace(A[r]);
}
if (st.size()) {
ans.emplace_back(flag ? *begin(st) : *rbegin(st)), flag ^= 1;
is_last[last_pos[ans.back()]] = 0;
while (A[l] != ans.back()) {
if (auto it = st.find(A[l++]); it != end(st)) st.erase(it);
}
st.erase(A[l++]); // no find
}
}
int M = ans.size();
cout << M << '\n';
for (int i = 0; i < M; ++i) cout << ans[i] + 1 << " \n"[i == M-1];
}
int32_t main() {
ios_base::sync_with_stdio(0), cin.tie(0);
int t = 1; cin >> t;
for (int _ = 1; _ <= t; ++_)
solve();
return 0;
}
2001E1 - Deterministic Heap (Easy Version)
idea & solution: Misuki
Consider subtask — decision version of the problem (i.e. yes/no problem) as follow: "Given a sequence $$$a$$$ resulting from $$$k$$$ operations, check whether such $$$a$$$ is a deterministic max-heap.", what property $$$a$$$ should have?
Try to fix the position of leaf being popped, what property are needed on the path from root to it?
Does it really matter where the leaf being popped lies important?
Try to count the number of $$$a$$$ where the first leaf being popped is fixed at one position using DP.
Try to use DP to track the path of elements being popped and count number of possible $$$a$$$ satisfy the property.
Again, in lot of problems, decision version of the problem is usually a useful subtask to consider. And it's especially useful in counting problems about giving some operation and ask you to count the number of possible outcomes.
Consider properties of the result sequence:
Since there may be multiple ways to apply operations to make the same heap, let's consider the decision version of the problem instead of counting the operation sequence directly. That is, "Given a sequence $$$a$$$ resulting from $$$k$$$ operations, check whether such $$$a$$$ is a deterministic max-heap.", and try to figure out what properties are needed.
Rephrase of problem:
Let $$$v = 2^{n - 1}$$$ be the only leaf such that after popping one element from the top, every element on the path between $$$1$$$ and $$$v$$$ would be moved upward, then the condition of a deterministic max-heap can be rephrased as follows:
- $$$a_1 = k$$$
- $$$a_{v} \ge a_{2v} + a_{2v + 1}$$$, for any $$$v$$$ ($$$1 \le v < 2^{n - 1}$$$)
- $$$a_{2\cdot 2^k} > a_{2 \cdot 2^k + 1}$$$, for any $$$k$$$ ($$$0 \le k \le n - 2$$$)
So we can see that for any $$$k$$$ ($$$0 \le k \le n - 2$$$), the number of operations done in the subtree of $$$2\cdot 2^k$$$ should be greater than the number of operations done in the subtree of $$$2 \cdot 2^k + 1$$$, and we don't care much about how these operations distribute in the subtree of $$$2 \cdot 2^k + 1$$$ as long as 3. holds. Let's call such subtree "uncritical".
Apply counting:
For any uncritical subtree with size $$$sz$$$, if we do $$$x$$$ operations under it, there are $$$\binom{x + (sz - 1)}{x}$$$ ways to do so.
Now we can use dp to consider all valid $$$a$$$ we can get by enumerating the number of operation done on each vertex on the path from $$$1$$$ to $$$2^{n - 1}$$$ and all uncritical subtree.
Let $$$dp[i][j]$$$ be the number of different $$$a$$$ we can get by $$$j$$$ operations on the subtree with size $$$2^i - 1$$$, then we have
base case: $$$dp[1][j] = 1, \forall j \in [0, k]$$$
transition: $$$dp[i + 1][l] \text{ += } dp[i][j] \times \binom{x + (2^i - 2)}{x} ,\forall x \in [0, j), l \in [j + x, k]$$$
using prefix sum, we can optimize the above dp to $$$O(nk^2)$$$, and the number of deterministic max-heap where vertex $$$2^{n - 1}$$$ would be pulled up is $$$dp[n][k]$$$.
Make use of symmetry:
Finally, due to the symmetry property of a perfect binary tree, the number of deterministic max-heap where $$$v$$$ would be pulled are equal for all possible $$$v$$$, so the final answer we want would be $$$dp[n][k] \times 2^{n - 1}$$$.
#include <iostream>
#include <vector>
using namespace std;
using ll = long long;
int binpow(ll a, ll b, ll p) {
ll c = 1;
while(b) {
if (b & 1) c = c * a % p;
a = a * a % p, b >>= 1;
}
return c;
}
int main() {
int t; cin >> t;
while(t--) {
int n, k, p; cin >> n >> k >> p;
vector<ll> fac(k + 1, 1);
for(int i = 1; i <= k; i++) fac[i] = fac[i - 1] * i % p;
vector<ll> faci(k + 1);
faci[k] = binpow(fac[k], p - 2, p);
for(int i = k - 1; i >= 0; i--) faci[i] = faci[i + 1] * (i + 1) % p;
vector<ll> pow2(n + 1, 1);
for(int i = 1; i <= n; i++) pow2[i] = pow2[i - 1] * 2 % p;
vector<ll> dp(k + 1, 1);
for(int i = 1; i < n; i++) {
vector<ll> binom(k + 1, 1);
for(int j = 1; j <= k; j++) binom[j] = binom[j - 1] * (pow2[i] + j - 2 + p) % p;
for(int j = 0; j <= k; j++) binom[j] = binom[j] * faci[j] % p;
vector<ll> nxt(k + 1);
for(int j = 0; j <= k; j++)
for(int x = 0; x < j and j + x <= k; x++)
nxt[j + x] = (nxt[j + x] + dp[j] * binom[x] % p) % p;
for(int j = 1; j <= k; j++)
nxt[j] = (nxt[j - 1] + nxt[j]) % p;
dp.swap(nxt);
}
cout << dp[k] * pow2[n - 1] % p << '\n';
}
}
2001E2 - Deterministic Heap (Hard Version)
idea & solution: Misuki
Fix the position of first and second leaf being popped, what's the property needed for $$$a$$$ to be determinitic?
Does the position of first leaf being popped really matters?
Fix the position of first leaf being popped, do we really need to consider all possible position of second leaf being popped?
Make good use of symmetry can reduce the complexity of problem significantly!
Make use of symmetry:
For convenience, let $$$\text{det_heap}()$$$ denote # twice-deterministic heap, $$$\text{det_heap}(v)$$$ denote # twice-deterministic heap where the first pop come from leaf $$$v$$$, $$$\text{det_heap}(v, u)$$$ denote # twice-deterministic heap where the first pop come from leaf $$$v$$$, second pop come from leaf $$$u$$$.
Similar to easier version, we have $$$\text{det_heap}() = 2^{n - 1}\cdot\text{det_heap}(2^{n - 1})$$$ because of symmetry.
Then consider enumerate $$$u$$$, the second leaf being popped, we have $$$\text{det_heap}(2^{n - 1}) = \sum\limits_{u = 2^{n - 1} + 1}^{2^n - 1}\text{det_heap}(2^{n - 1}, u)$$$
because of symmetry, again, for any $$$u_1 \neq u_2, LCA(2^{n - 1}, u_1) = LCA(2^{n - 1}, u_2)$$$, we have $$$\text{det_heap}(2^{n - 1}, u_1) = \text{det_heap}(2^{n - 1}, u_2)$$$, so for each LCA, we only need to enumerate leftmost leaf under it as second popped leaf and multiply answer with # leaves in such subtree.
Rephrase of Problem:
then consider the relation of values between vertices, we have
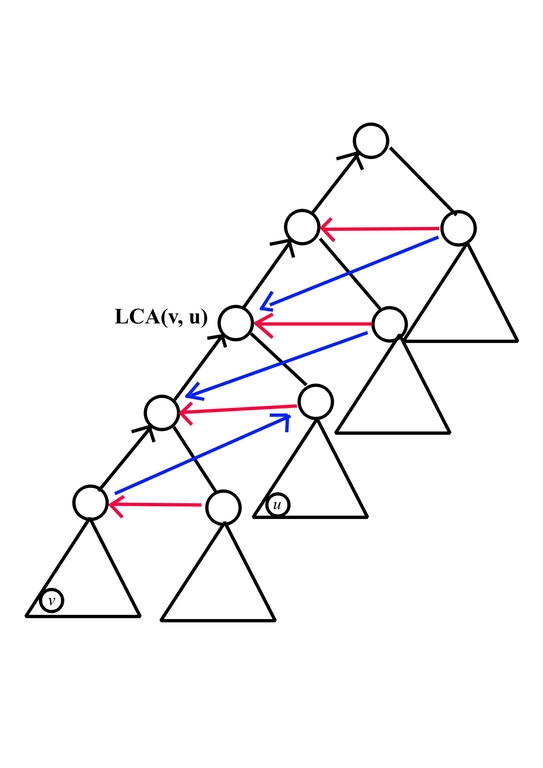
where
- black edge from $$$x$$$ to $$$y$$$ means $$$a_x \le a_y$$$, which comes from the nature of $$$\text{add}$$$ operation
- red edge from $$$x$$$ to $$$y$$$ means $$$a_x < a_y$$$, which come from the fact that $$$v$$$ should be first leaf being pulled
- blue edge from $$$x$$$ to $$$y$$$ means $$$a_x < a_y$$$, which come from the fact that $$$u$$$ should be second leaf being pulled
Eliminate Useless Conditions:
Then observe if we have some directed triangle consist of edges $$$(x, y), (y, z), (x, z)$$$, edge $$$(x, z)$$$ didn't bring extra relation so we can delete it, after that, we would have
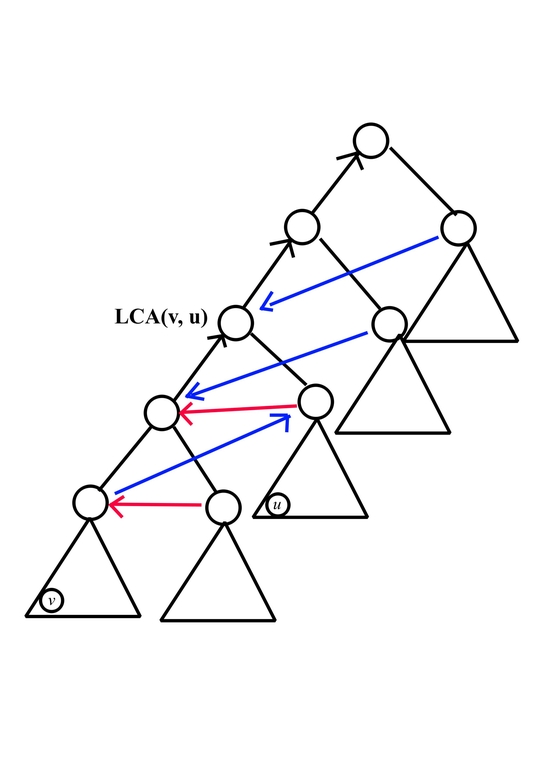
Applying Counting:
Then we can use pair of value of vertices from same depth as the state of dp, and enumerate such pair in increasing order of height while not breaking the relations, then we would have $$$dp[h][l][r]$$$ = # twice-deterministic heap when the left vertex have value $$$l$$$ and right vertex have value $$$r$$$ and the current height is $$$h$$$.
First, to handle the relation of Z shape formed by red/blue arrows and enumerate value of $$$(L, R, R')$$$, consider the following picture
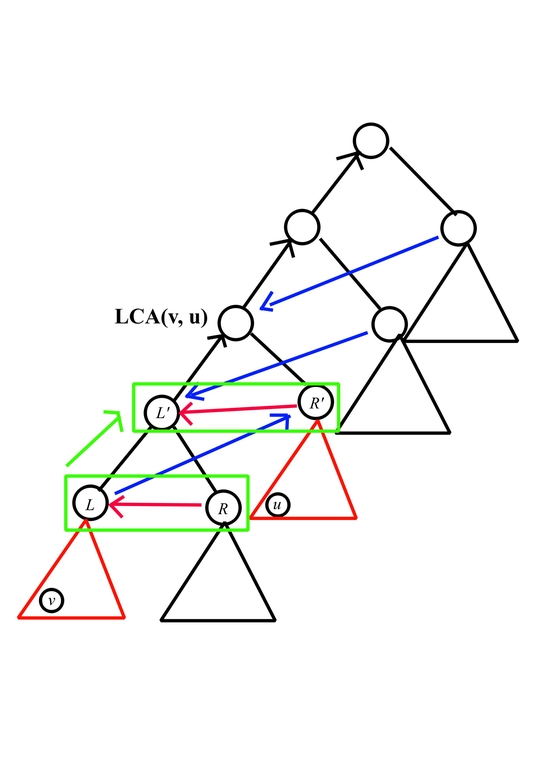
(The red subtree is one-time deterministic heap, while the other can be any heap.)
Also let $$$f(h, k)$$$ denote # deterministic heap for one time pop with height $$$h$$$ after doing operation $$$k$$$ times where the leftmost leaf being pulled, $$$g(h, k)$$$ denote # max heap with height $$$h$$$ after doing operation $$$k$$$ times (We already know how to compute them in easier version of this problem)
Let's fix the value $$$L$$$ and $$$R$$$, and push it to some $$$dp[h][L'][R']$$$, we need to satisfy
- $$$L' > R' > L > R$$$
- $$$L' \ge L + R$$$
in such case, enumerate all pair $$$(L, R), (L > R)$$$ and for all $$$L' \ge L + R, R' \ge L + 1$$$, add $$$f(h - 1, L) \cdot g(h - 1, R)$$$ to $$$dp[h][L'][R']$$$. After that, for every $$$L' \le R'$$$, eliminate its contribution, while for every $$$L' > R'$$$, multiply its contribution with $$$f(h, R') \cdot 2^h$$$. which can be done in $$$O(k^2)$$$ with the help of prefix sum.
Second, to handle the relation formed by black/blue edges and enumerate value $$$R'$$$, consider the following picture
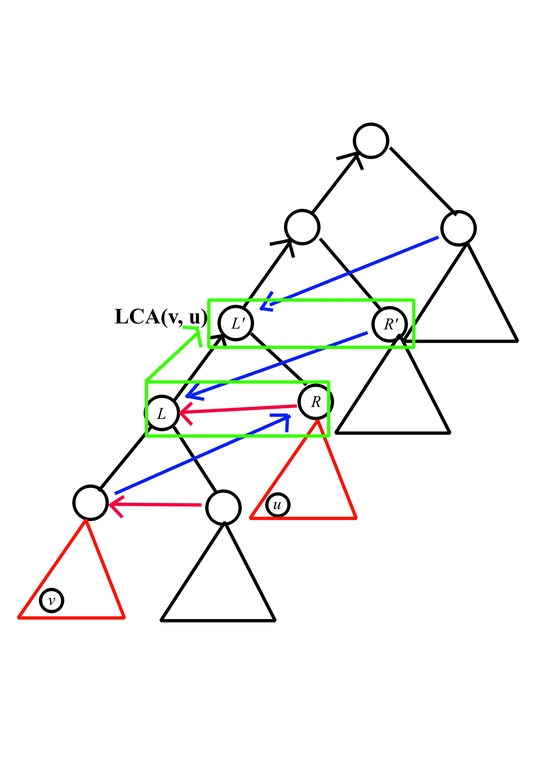
For each $$$L, R$$$, we need to push it some some $$$dp[h][L'][R']$$$ where the following conditions hold
- $$$L' \ge L > R'$$$
- $$$L' \ge L + R$$$
we can handle it by first adding $$$dp[h - 1][L][R]$$$ to $$$dp[L'][R']$$$ for all $$$L' \ge L + R, R' \le L - 1$$$. Then for all $$$L' \le R'$$$, eliminate its contribution, while for the other, multiply the contribution with $$$g(h, R')$$$, which can also be done by prefix sum in $$$O(k^2)$$$.
Then the answer would be $$$2^{n - 1} \cdot \sum\limits_{L + R \le k}dp[h - 2][L][R]$$$ and the problem has been solved in $$$O(nk^2)$$$.
#include <iostream>
#include <vector>
using namespace std;
using ll = long long;
int binpow(ll a, ll b, ll p) {
ll c = 1;
while(b) {
if (b & 1) c = c * a % p;
a = a * a % p, b >>= 1;
}
return c;
}
int main() {
int t; cin >> t;
while(t--) {
int n, k, p; cin >> n >> k >> p;
vector<ll> fac(k + 1, 1);
for(int i = 1; i <= k; i++) fac[i] = fac[i - 1] * i % p;
vector<ll> faci(k + 1);
faci[k] = binpow(fac[k], p - 2, p);
for(int i = k - 1; i >= 0; i--) faci[i] = faci[i + 1] * (i + 1) % p;
vector<ll> pow2(n + 1, 1);
for(int i = 1; i <= n; i++) pow2[i] = pow2[i - 1] * 2 % p;
vector<ll> dp(k + 1, 1);
vector dp2(k + 1, vector<ll>(k + 1));
for(int l = 0; l <= k; l++)
for(int r = 0; r < l; r++)
dp2[l][r] = 1;
for(int i = 1; i + 1 < n; i++) {
vector<ll> binom(k + 1, 1);
for(int j = 1; j <= k; j++) binom[j] = binom[j - 1] * (pow2[i] + j - 2 + p) % p;
for(int j = 0; j <= k; j++) binom[j] = binom[j] * faci[j] % p;
vector<ll> binom2(k + 1, 1);
for(int j = 1; j <= k; j++) binom2[j] = binom2[j - 1] * (pow2[i + 1] + j - 2 + p) % p;
for(int j = 0; j <= k; j++) binom2[j] = binom2[j] * faci[j] % p;
vector<ll> nxt(k + 1);
for(int j = 0; j <= k; j++)
for(int x = 0; x < j and j + x <= k; x++)
nxt[j + x] = (nxt[j + x] + dp[j] * binom[x] % p) % p;
for(int j = 1; j <= k; j++)
nxt[j] = (nxt[j - 1] + nxt[j]) % p;
vector nxt2(k + 1, vector<ll>(k + 1));
{
vector tmp(k + 1, vector<ll>(k + 1));
for(int l = 0; l < k; l++)
for(int r = 0; r < l and l + r <= k; r++)
tmp[l + r][l + 1] = (tmp[l + r][l + 1] + dp[l] * binom[r]) % p;
for(int l = 0; l <= k; l++)
for(int r = 1; r <= k; r++)
tmp[l][r] = (tmp[l][r] + tmp[l][r - 1]) % p;
for(int l = 1; l <= k; l++)
for(int r = 1; r <= k; r++)
tmp[l][r] = (tmp[l][r] + tmp[l - 1][r]) % p;
for(int l = 0; l <= k; l++)
for(int r = 0; r < l; r++)
nxt2[l][r] = (nxt2[l][r] + tmp[l][r] * nxt[r] % p * pow2[i]) % p;
}
{
vector tmp(k + 1, vector<ll>(k + 1));
for(int l = 1; l <= k; l++)
for(int r = 0; l + r <= k; r++)
tmp[l + r][l - 1] = (tmp[l + r][l - 1] + dp2[l][r]) % p;
for(int l = 0; l <= k; l++)
for(int r = k - 1; r >= 0; r--)
tmp[l][r] = (tmp[l][r] + tmp[l][r + 1]) % p;
for(int l = 1; l <= k; l++)
for(int r = 0; r <= k; r++)
tmp[l][r] = (tmp[l][r] + tmp[l - 1][r]) % p;
for(int l = 0; l <= k; l++)
for(int r = 0; r <= k; r++)
nxt2[l][r] = (nxt2[l][r] + tmp[l][r] * binom2[r]) % p;
}
dp.swap(nxt);
dp2.swap(nxt2);
}
ll ans = 0;
for(int l = 0; l <= k; l++)
for(int r = 0; l + r <= k; r++)
ans = (ans + dp2[l][r]) % p;
cout << ans * pow2[n - 1] % p << '\n';
}
}










