What's the most obvious lower bound of the answer?

Is the lower bound achievable?

One standard way to solve optimization problem is to make observation on lower(upper) bound of the answer and prove such bound is achievable, it's useful in lot of problems.

Let $$$x$$$ be one of the most frequent elements in $$$a$$$, then the answer must be at least $$$(n - \text{frequency of } x)$$$, and this lower bound is always achievable by keep erasing a non-$$$x$$$ element from $$$a$$$, and we can prove it's always possible to do so.

proof:

If all elements of $$$a$$$ are $$$x$$$, we are done. Otherwise, let $$$y$$$ denote all the elements that are not $$$x$$$, then $$$a$$$ would have some subarray of the form $$$x \ldots x, y \ldots y, x \ldots x$$$. In this subarray, there must exist adjacent elements that satisfy $$$a_i \leq a_{(i \bmod m) + 1}$$$, otherwise we would have $$$x > y > \ldots > y > x$$$ implying $$$x > x$$$ which leads to a contradiction.

#include <algorithm>
#include <iostream>
#include <vector>

using namespace std;

int main() {
  ios::sync_with_stdio(false), cin.tie(NULL);

  int t; cin >> t;
  while(t--) {
    int n; cin >> n;
    vector<int> a(n);
    for(int &x : a) cin >> x;

    vector<int> freq(n + 1);
    for(int x : a) freq[x]++;

    cout << n - (*max_element(freq.begin(), freq.end())) << '\n';
  }
}

Consider the cost function:

Let $$$c_1, c_2$$$ denote the minimum number of carriage return operations needed to make $$$a = p$$$ if Misuki is using first/second typewritter. Let's consider how to calculate them.

For $$$c_1$$$, we need to do carriage return operation whenever the position of value $$$x + 1$$$ is before $$$x$$$, for all $$$x \in [1, n - 1]$$$, so $$$c_1 = (\text{#}x \in [1, n - 1] \text{ such that } \mathrm{pos}_x > \mathrm{pos}_{x + 1})$$$.

Similarly, $$$c_2 = (\text{#}x \in [1, n - 1] \text{ such that } \mathrm{pos}_x < \mathrm{pos}_{x + 1})$$$.

Since for $$$x \in [1, n - 1]$$$, either $$$\mathrm{pos}_x < \mathrm{pos}_{x + 1}$$$ or $$$\mathrm{pos}_x > \mathrm{pos}_{x + 1}$$$ would hold, so we have $$$c_1 + c_2 = n - 1$$$, which is a constant, and $$$c_1 = c_2 \leftrightarrow c_1 = \frac{n - 1}{2}$$$, which only has solution when $$$n$$$ is odd, and such $$$p$$$ can be constructed easily (for example, $$${n - 1, n, n - 3, n - 2, ..., 4, 5, 2, 3, 1}$$$).

#include <iostream>
#include <numeric>
#include <vector>

using namespace std;

int main() {
  ios::sync_with_stdio(false), cin.tie(NULL);

  int t; cin >> t;
  while(t--) {
    int n; cin >> n;
    if (n % 2 == 0) {
      cout << -1 << '\n';
    } else {
      vector<int> p(n);
      iota(p.begin(), p.end(), 1);
      for(int i = 1; i < n; i += 2)
        swap(p[i], p[i + 1]);
      for(int i = 0; i < n; i++)
        cout << p[i] << " \n"[i + 1 == n];
    }
  }
}

Imagine we have $$$n$$$ isolated vertices initially, can you find any edge connect two component using reasonable number of queries?

Use binary search.

It's easy to verify that querying $$$a$$$ and $$$b$$$ will return the midpoint of the path between $$$a$$$ and $$$b$$$. In case the path has odd length, the node closer to $$$a$$$ of the two central nodes will be returned.

We will now construct the tree by expanding a connected component. Let $$$A = \{1\}$$$ and $$$B = \{2,\ldots,n\}$$$. While $$$B$$$ is not empty, choose any $$$b \in B$$$ and $$$a \in A$$$. Let $$$P$$$ be the path between $$$a$$$ and $$$b$$$. By construction, $$$P$$$ will consist of a prefix contained in $$$A$$$ and a suffix contained in $$$B$$$. We can binary search for the first $$$i$$$ such that $$$P_i \in B$$$.
This will take at most $$$\lceil log(|P|) \rceil + 2$$$ queries. Then, $$$(P_{i-1}, P_i)$$$ will be an edge of the tree, so we will set $$$A = A \cup {P_i}$$$ and $$$B = B \backslash {P_i}$$$.

The total number of queries will be smaller than $$$n \lceil log(n) \rceil + 2n = 12000$$$.

Consider we have $$$n$$$ isolated vertices initially, and try to keep finding an edge connect two different component.

Assume $$$u, v$$$ is at different component, then we have the following possible cases for the answer $$$x$$$.

1. $$$x = u$$$: which means $$$u, v$$$ are connected by an edge and we are done.
2. $$$x$$$ belongs to same component of $$$u$$$, seting $$$u := x$$$.
3. $$$x$$$ belongs to same component of $$$v$$$, seting $$$v := x$$$.
4. $$$x$$$ belongs to other component than $$$u, v$$$, in such case, either setting $$$u := x$$$ or $$$v := x$$$.

in case 1. we are done, and in case 2, 3, 4, we shorten the distance between $$$u, v$$$ by about half while keeping them not belongs to same component, so we can find an edge connect two component in $$$O(\lg n)$$$ queries and we are done.

#include <iostream>
#include <system_error>
#include <vector>
using namespace std;
 
int qry(int a, int b){
    cout << "? " << a+1 << ' ' << b+1 << endl;
    fflush(stdout);
    int r; cin >> r;
    return r-1;
}
 
void solve(){
    int N; cin >> N;
    vector<int> in_tree(N, 0), stk;
    for (size_t i = 1; i < N; ++i)
        stk.push_back(i);
    in_tree[0] = 1;
 
    vector<pair<int, int>> edges;
 
    while(!stk.empty()){
        int n = stk.back();
        stk.pop_back();
        if(in_tree[n])continue;
        int l = 0, r = n;
        while(1){
            int q = qry(l, r);
            if(q == l){
                in_tree[r] = 1;
                edges.push_back({l, r});
                break;
            }
            if(in_tree[q])l = q;
            else r = q;
        }
        stk.push_back(n);
    }
    cout << "! ";
    for(auto [x, y]: edges)cout << x+1 << ' ' << y+1 << ' ';
    cout << endl;
}
 
int main(){
    int t; cin >> t;
    while(t--)solve();
}

#include <iostream>
#include <numeric>
#include <vector>
#include <array>

using namespace std;

int query(int u, int v) {
  cout << "? " << u + 1 << ' ' << v + 1 << '\n';
  int x; cin >> x;
  return x - 1;
}

int main() {
  int t; cin >> t;
  while(t--) {
    int n; cin >> n;

    vector<array<int, 2>> e;
    vector<int> c(n);
    iota(c.begin(), c.end(), 0);
    auto addEdge = [&](int u, int v) {
      e.push_back({u, v});
      vector<int> cand;
      for(int i = 0; i < n; i++)
        if (c[i] == c[v])
          cand.emplace_back(i);
      for(int i : cand)
        c[i] = c[u];
    };

    for(int i = 0; i < n - 1; i++) {
      int u = 0, v = 0;
      while(c[v] == c[u]) v++;
      int x;
      while((x = query(u, v)) != u) {
        if (c[u] == c[x]) u = x;
        else v = x;
      }
      addEdge(u, v);
    }

    cout << "!";
    for(auto [u, v] : e) cout << ' ' << u + 1 << ' ' << v + 1;
    cout << '\n';
  }
}

Forget about minimize lexicographical order. What's the size of longest $$$b$$$ we can get?

It's the number of different elements. Try to minimize/maximize first element in $$$b$$$ without reducing the max size of $$$b$$$ we can get.

When solving problem asking for minimize/maximize lexicographical order of something, we can often construct them by minimize/maximize first element greedily.

Consider subtask:

Let's ignore the constraint where $$$b$$$ should be lexicographically smallest. How can we find the length of $$$b$$$?

Apparently, it is the number of distinct elements in $$$a$$$. Let's call it $$$k$$$.

Construct $$$b$$$ from left to right without worsening the answer:

Now we know how to find the maximum possible length of $$$b$$$. Let's try to construct $$$b$$$ from left to right without worsening the answer, and greedily minimize its lexicographical order. Assume we pick $$$a_i$$$ as the $$$j$$$-th element in $$$b$$$, then there should be $$$k - j$$$ distinct elements in the subarray $$$a[i + 1, n]$$$ after deleting all elements that appear in the subarray $$$b[1, j]$$$.

Assume we already construct $$$b_1, b_2, \ldots, b_j$$$ where $$$b_j = a_i$$$ and we want to find $$$b_{j + 1}$$$, and let $$$l_x$$$ be the last position where $$$x$$$ occurs in the subarray $$$a[i + 1, n]$$$ or $$$\infty$$$ if it doesn't exist, then we can choose anything in $$$a[i + 1, \min\limits_{1 \le x \le n}(l_x)]$$$. And to minimize lexicographical order, we need to choose the maximum element in it if $$$(j + 1)$$$ is odd, or the minimum element otherwise. If there are multiple of them, choose the leftmost one of them is optimal since we would have a longer suffix of $$$a$$$ for future construction.

Then observe for the candidate window (i.e. $$$a[i + 1, \min\limits_{1 \le x \le n}(l_x)]$$$), its left bound and right bound are non-decreasing, so we can use priority queues or set to maintain all possible candidates by storing $$$(a_{pos}, pos)$$$, and another priority queue or set to maintain all $$$l_x > i$$$. And the total time complexity is $$$O(nlgn)$$$.

#include <iostream>
#include <vector>
#include <queue>
#include <array>
#include <climits>

using namespace std;

int main() {
  ios::sync_with_stdio(false), cin.tie(0);

  int t; cin >> t;
  while(t--) {
    int n; cin >> n;
    vector<int> a(n);
    for(int &x : a) {
      cin >> x;
      x--;
    }

    vector l(n + 1, INT_MAX);
    for(int i = 0; i < n; i++)
      l[a[i]] = i;

    priority_queue<int, vector<int>, greater<int>> ls(l.begin(), l.end());
    priority_queue<array<int, 2>, vector<array<int, 2>>, greater<array<int, 2>>> mx_cand, mn_cand;
    vector<bool> used(n, false);

    for(int i = 0; i <= ls.top(); i++) {
      mx_cand.push({-a[i], i});
      mn_cand.push({a[i], i});
    }

    vector<int> b;
    int i = 0;
    while(!mn_cand.empty()) {
      auto [x, pos] = (b.size() % 2 == 0 ? mx_cand.top() : mn_cand.top());
      if (b.size() % 2 == 0) {
        mx_cand.pop();
        x *= -1;
      } else {
        mn_cand.pop();
      }
      b.emplace_back(x);
      i = pos + 1, used[x] = true;
      while(ls.top() != INT_MAX and used[a[ls.top()]]) {
        int j = ls.top(); ls.pop();
        for(int k = j + 1; k <= min(ls.top(), n - 1); k++) {
          mx_cand.push({-a[k], k});
          mn_cand.push({a[k], k});
        }
      }
      while(!mx_cand.empty() and (used[-mx_cand.top()[0]] or mx_cand.top()[1] < i)) mx_cand.pop();
      while(!mn_cand.empty() and (used[mn_cand.top()[0]] or mn_cand.top()[1] < i)) mn_cand.pop();
    }

    cout << b.size() << '\n';
    for(int i = 0; i < b.size(); i++)
      cout << b[i] + 1 << " \n"[i + 1 == b.size()];
  }
}

#include <cstdint>
#include <iostream>
#include <set>
#include <vector>

using namespace std;

void solve() {
    int N; cin >> N;
    
    vector<int> A(N);
    for (int &x : A) cin >> x, --x;
    
    vector<int> cnt(N, 0), is_last(N, 0), last_pos(N, -1);
    for (int i = N-1; i >= 0; --i) {
        if (!cnt[A[i]]++) is_last[i] = 1, last_pos[A[i]] = i;
    }
    
    vector<int> ans;
    multiset<int> st;
    int l = 0, r = -1, flag = 0;
    while (r+1 < N) {
        while (r+1 < N and (r == -1 or !is_last[r])) {
            ++r;
            if (is_last[last_pos[A[r]]]) st.emplace(A[r]);
        }
        if (st.size()) {
            ans.emplace_back(flag ? *begin(st) : *rbegin(st)), flag ^= 1;
            is_last[last_pos[ans.back()]] = 0;
            while (A[l] != ans.back()) {
                if (auto it = st.find(A[l++]); it != end(st)) st.erase(it);
            }
            st.erase(A[l++]); // no find
        }
    }
    
    int M = ans.size();
    cout << M << '\n';
    for (int i = 0; i < M; ++i) cout << ans[i] + 1 << " \n"[i == M-1];
}

int32_t main() {
    ios_base::sync_with_stdio(0), cin.tie(0);
    
    int t = 1; cin >> t;
    for (int _ = 1; _ <= t; ++_)
        solve();
    
    return 0;
}

Consider subtask — decision version of the problem (i.e. yes/no problem) as follow: "Given a sequence $$$a$$$ resulting from $$$k$$$ operations, check whether such $$$a$$$ is a deterministic max-heap.", what property $$$a$$$ should have?

Try to fix the position of leaf being popped, what property are needed on the path from root to it?

Again, in lot of problems, decision version of the problem is usually a useful subtask to consider. And it's especially useful in counting problems about giving some operation and ask you to count the number of possible outcomes.

Consider properties of the result sequence:

Since there may be multiple ways to apply operations to make the same heap, let's consider the decision version of the problem instead of counting the operation sequence directly. That is, "Given a sequence $$$a$$$ resulting from $$$k$$$ operations, check whether such $$$a$$$ is a deterministic max-heap.", and try to figure out what properties are needed.

Rephrase of problem:

Let $$$v = 2^{n - 1}$$$ be the only leaf such that after popping one element from the top, every element on the path between $$$1$$$ and $$$v$$$ would be moved upward, then the condition of a deterministic max-heap can be rephrased as follows:

1. $$$a_1 = k$$$
2. $$$a_{v} \ge a_{2v} + a_{2v + 1}$$$, for any $$$v$$$ ($$$1 \le v < 2^{n - 1}$$$)
3. $$$a_{2\cdot 2^k} > a_{2 \cdot 2^k + 1}$$$, for any $$$k$$$ ($$$0 \le k \le n - 2$$$)

So we can see that for any $$$k$$$ ($$$0 \le k \le n - 2$$$), the number of operations done in the subtree of $$$2\cdot 2^k$$$ should be greater than the number of operations done in the subtree of $$$2 \cdot 2^k + 1$$$, and we don't care much about how these operations distribute in the subtree of $$$2 \cdot 2^k + 1$$$ as long as 3. holds. Let's call such subtree "uncritical".

Apply counting:

For any uncritical subtree with size $$$sz$$$, if we do $$$x$$$ operations under it, there are $$$\binom{x + (sz - 1)}{x}$$$ ways to do so.

Now we can use dp to consider all valid $$$a$$$ we can get by enumerating the number of operation done on each vertex on the path from $$$1$$$ to $$$2^{n - 1}$$$ and all uncritical subtree.

Let $$$dp[i][j]$$$ be the number of different $$$a$$$ we can get by $$$j$$$ operations on the subtree with size $$$2^i - 1$$$, then we have

base case: $$$dp[1][j] = 1, \forall j \in [0, k]$$$

transition: $$$dp[i + 1][l] \text{ += } dp[i][j] \times \binom{x + (2^i - 2)}{x} ,\forall x \in [0, j), l \in [j + x, k]$$$

using prefix sum, we can optimize the above dp to $$$O(nk^2)$$$, and the number of deterministic max-heap where vertex $$$2^{n - 1}$$$ would be pulled up is $$$dp[n][k]$$$.

Make use of symmetry:

Finally, due to the symmetry property of a perfect binary tree, the number of deterministic max-heap where $$$v$$$ would be pulled are equal for all possible $$$v$$$, so the final answer we want would be $$$dp[n][k] \times 2^{n - 1}$$$.

#include <iostream>
#include <vector>

using namespace std;

using ll = long long;

int binpow(ll a, ll b, ll p) {
  ll c = 1;
  while(b) {
    if (b & 1) c = c * a % p;
    a = a * a % p, b >>= 1;
  }
  return c;
}

int main() {
  int t; cin >> t;
  while(t--) {
    int n, k, p; cin >> n >> k >> p;

    vector<ll> fac(k + 1, 1);
    for(int i = 1; i <= k; i++) fac[i] = fac[i - 1] * i % p;

    vector<ll> faci(k + 1);
    faci[k] = binpow(fac[k], p - 2, p);
    for(int i = k - 1; i >= 0; i--) faci[i] = faci[i + 1] * (i + 1) % p;

    vector<ll> pow2(n + 1, 1);
    for(int i = 1; i <= n; i++) pow2[i] = pow2[i - 1] * 2 % p;

    vector<ll> dp(k + 1, 1);
    for(int i = 1; i < n; i++) {
      vector<ll> binom(k + 1, 1);
      for(int j = 1; j <= k; j++) binom[j] = binom[j - 1] * (pow2[i] + j - 2 + p) % p;
      for(int j = 0; j <= k; j++) binom[j] = binom[j] * faci[j] % p;

      vector<ll> nxt(k + 1);
      for(int j = 0; j <= k; j++)
        for(int x = 0; x < j and j + x <= k; x++)
          nxt[j + x] = (nxt[j + x] + dp[j] * binom[x] % p) % p;

      for(int j = 1; j <= k; j++)
        nxt[j] = (nxt[j - 1] + nxt[j]) % p;
      dp.swap(nxt);
    }

    cout << dp[k] * pow2[n - 1] % p << '\n';
  }
}

Fix the position of first and second leaf being popped, what's the property needed for $$$a$$$ to be determinitic?

Does the position of first leaf being popped really matters?

Fix the position of first leaf being popped, do we really need to consider all possible position of second leaf being popped?

Make good use of symmetry can reduce the complexity of problem significantly!

Make use of symmetry:

For convenience, let $$$\text{det_heap}()$$$ denote # twice-deterministic heap, $$$\text{det_heap}(v)$$$ denote # twice-deterministic heap where the first pop come from leaf $$$v$$$, $$$\text{det_heap}(v, u)$$$ denote # twice-deterministic heap where the first pop come from leaf $$$v$$$, second pop come from leaf $$$u$$$.

Similar to easier version, we have $$$\text{det_heap}() = 2^{n - 1}\cdot\text{det_heap}(2^{n - 1})$$$ because of symmetry.

Then consider enumerate $$$u$$$, the second leaf being popped, we have $$$\text{det_heap}(2^{n - 1}) = \sum\limits_{u = 2^{n - 1} + 1}^{2^n - 1}\text{det_heap}(2^{n - 1}, u)$$$

because of symmetry, again, for any $$$u_1 \neq u_2, LCA(2^{n - 1}, u_1) = LCA(2^{n - 1}, u_2)$$$, we have $$$\text{det_heap}(2^{n - 1}, u_1) = \text{det_heap}(2^{n - 1}, u_2)$$$, so for each LCA, we only need to enumerate leftmost leaf under it as second popped leaf and multiply answer with # leaves in such subtree.

Rephrase of Problem:

then consider the relation of values between vertices, we have

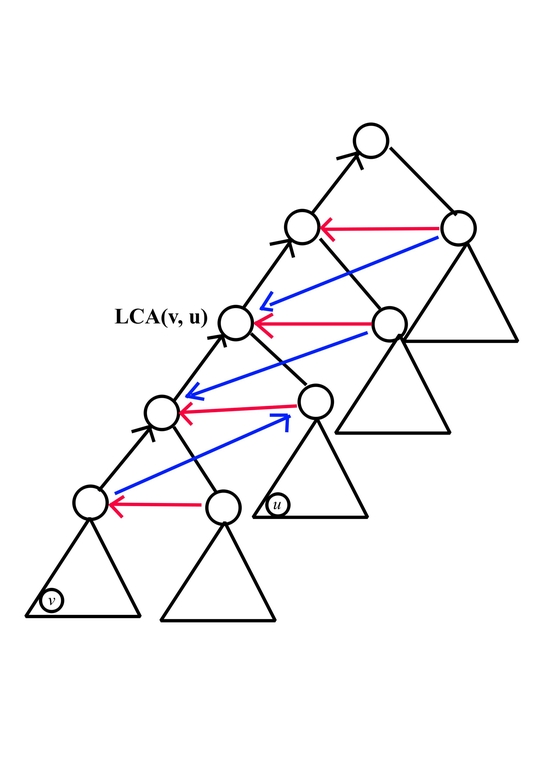
where

• black edge from $$$x$$$ to $$$y$$$ means $$$a_x \le a_y$$$, which comes from the nature of $$$\text{add}$$$ operation
• red edge from $$$x$$$ to $$$y$$$ means $$$a_x < a_y$$$, which come from the fact that $$$v$$$ should be first leaf being pulled
• blue edge from $$$x$$$ to $$$y$$$ means $$$a_x < a_y$$$, which come from the fact that $$$u$$$ should be second leaf being pulled

Eliminate Useless Conditions:

Then observe if we have some directed triangle consist of edges $$$(x, y), (y, z), (x, z)$$$, edge $$$(x, z)$$$ didn't bring extra relation so we can delete it, after that, we would have

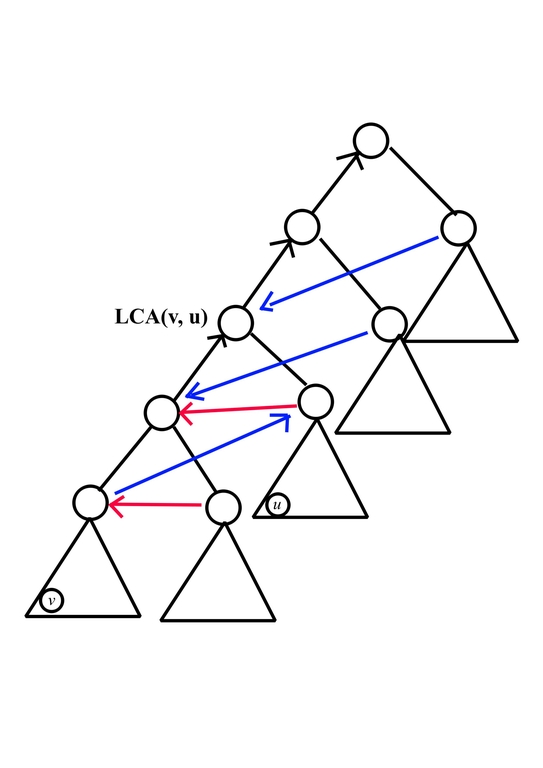
Applying Counting:

Then we can use pair of value of vertices from same depth as the state of dp, and enumerate such pair in increasing order of height while not breaking the relations, then we would have $$$dp[h][l][r]$$$ = # twice-deterministic heap when the left vertex have value $$$l$$$ and right vertex have value $$$r$$$ and the current height is $$$h$$$.

First, to handle the relation of Z shape formed by red/blue arrows and enumerate value of $$$(L, R, R')$$$, consider the following picture

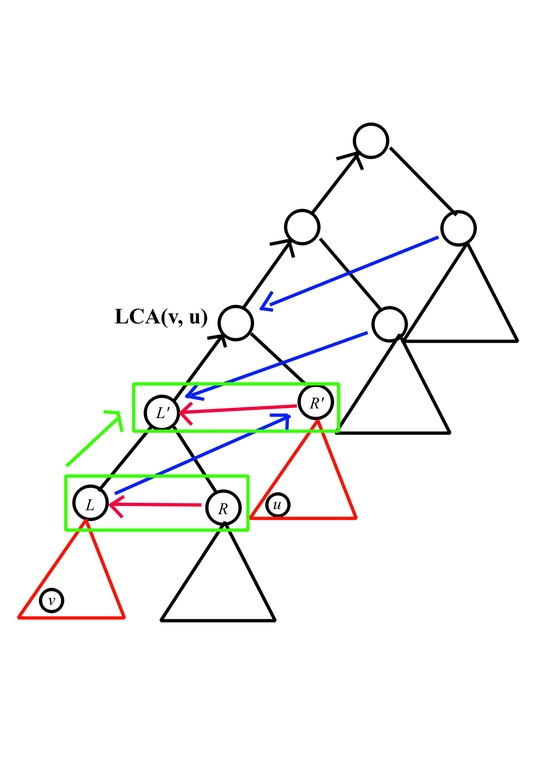
(The red subtree is one-time deterministic heap, while the other can be any heap.)

Also let $$$f(h, k)$$$ denote # deterministic heap for one time pop with height $$$h$$$ after doing operation $$$k$$$ times where the leftmost leaf being pulled, $$$g(h, k)$$$ denote # max heap with height $$$h$$$ after doing operation $$$k$$$ times (We already know how to compute them in easier version of this problem)

Let's fix the value $$$L$$$ and $$$R$$$, and push it to some $$$dp[h][L'][R']$$$, we need to satisfy

• $$$L' > R' > L > R$$$
• $$$L' \ge L + R$$$

in such case, enumerate all pair $$$(L, R), (L > R)$$$ and for all $$$L' \ge L + R, R' \ge L + 1$$$, add $$$f(h - 1, L) \cdot g(h - 1, R)$$$ to $$$dp[h][L'][R']$$$. After that, for every $$$L' \le R'$$$, eliminate its contribution, while for every $$$L' > R'$$$, multiply its contribution with $$$f(h, R') \cdot 2^h$$$. which can be done in $$$O(k^2)$$$ with the help of prefix sum.

Second, to handle the relation formed by black/blue edges and enumerate value $$$R'$$$, consider the following picture

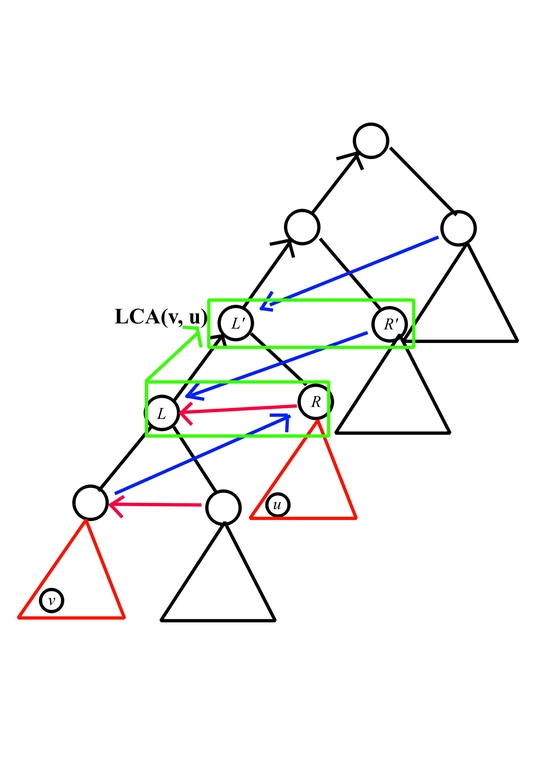
For each $$$L, R$$$, we need to push it some some $$$dp[h][L'][R']$$$ where the following conditions hold

• $$$L' \ge L > R'$$$
• $$$L' \ge L + R$$$

we can handle it by first adding $$$dp[h - 1][L][R]$$$ to $$$dp[L'][R']$$$ for all $$$L' \ge L + R, R' \le L - 1$$$. Then for all $$$L' \le R'$$$, eliminate its contribution, while for the other, multiply the contribution with $$$g(h, R')$$$, which can also be done by prefix sum in $$$O(k^2)$$$.

Then the answer would be $$$2^{n - 1} \cdot \sum\limits_{L + R \le k}dp[h - 2][L][R]$$$ and the problem has been solved in $$$O(nk^2)$$$.

#include <iostream>
#include <vector>

using namespace std;

using ll = long long;

int binpow(ll a, ll b, ll p) {
  ll c = 1;
  while(b) {
    if (b & 1) c = c * a % p;
    a = a * a % p, b >>= 1;
  }
  return c;
}

int main() {
  int t; cin >> t;
  while(t--) {
    int n, k, p; cin >> n >> k >> p;

    vector<ll> fac(k + 1, 1);
    for(int i = 1; i <= k; i++) fac[i] = fac[i - 1] * i % p;

    vector<ll> faci(k + 1);
    faci[k] = binpow(fac[k], p - 2, p);
    for(int i = k - 1; i >= 0; i--) faci[i] = faci[i + 1] * (i + 1) % p;

    vector<ll> pow2(n + 1, 1);
    for(int i = 1; i <= n; i++) pow2[i] = pow2[i - 1] * 2 % p;

    vector<ll> dp(k + 1, 1);
    vector dp2(k + 1, vector<ll>(k + 1));
    for(int l = 0; l <= k; l++)
      for(int r = 0; r < l; r++)
        dp2[l][r] = 1;
    for(int i = 1; i + 1 < n; i++) {
      vector<ll> binom(k + 1, 1);
      for(int j = 1; j <= k; j++) binom[j] = binom[j - 1] * (pow2[i] + j - 2 + p) % p;
      for(int j = 0; j <= k; j++) binom[j] = binom[j] * faci[j] % p;

      vector<ll> binom2(k + 1, 1);
      for(int j = 1; j <= k; j++) binom2[j] = binom2[j - 1] * (pow2[i + 1] + j - 2 + p) % p;
      for(int j = 0; j <= k; j++) binom2[j] = binom2[j] * faci[j] % p;

      vector<ll> nxt(k + 1);
      for(int j = 0; j <= k; j++)
        for(int x = 0; x < j and j + x <= k; x++)
          nxt[j + x] = (nxt[j + x] + dp[j] * binom[x] % p) % p;

      for(int j = 1; j <= k; j++)
        nxt[j] = (nxt[j - 1] + nxt[j]) % p;

      vector nxt2(k + 1, vector<ll>(k + 1));
      {
        vector tmp(k + 1, vector<ll>(k + 1));
        for(int l = 0; l < k; l++)
          for(int r = 0; r < l and l + r <= k; r++)
            tmp[l + r][l + 1] = (tmp[l + r][l + 1] + dp[l] * binom[r]) % p;
        for(int l = 0; l <= k; l++)
          for(int r = 1; r <= k; r++)
            tmp[l][r] = (tmp[l][r] + tmp[l][r - 1]) % p;
        for(int l = 1; l <= k; l++)
          for(int r = 1; r <= k; r++)
            tmp[l][r] = (tmp[l][r] + tmp[l - 1][r]) % p;
        for(int l = 0; l <= k; l++)
          for(int r = 0; r < l; r++)
            nxt2[l][r] = (nxt2[l][r] + tmp[l][r] * nxt[r] % p * pow2[i]) % p;
      }

      {
        vector tmp(k + 1, vector<ll>(k + 1));
        for(int l = 1; l <= k; l++)
          for(int r = 0; l + r <= k; r++)
            tmp[l + r][l - 1] = (tmp[l + r][l - 1] + dp2[l][r]) % p;
        for(int l = 0; l <= k; l++)
          for(int r = k - 1; r >= 0; r--)
            tmp[l][r] = (tmp[l][r] + tmp[l][r + 1]) % p;
        for(int l = 1; l <= k; l++)
          for(int r = 0; r <= k; r++)
            tmp[l][r] = (tmp[l][r] + tmp[l - 1][r]) % p;
        for(int l = 0; l <= k; l++)
          for(int r = 0; r <= k; r++)
            nxt2[l][r] = (nxt2[l][r] + tmp[l][r] * binom2[r]) % p;
      }

      dp.swap(nxt);
      dp2.swap(nxt2);
    }

    ll ans = 0;
    for(int l = 0; l <= k; l++)
      for(int r = 0; l + r <= k; r++)
        ans = (ans + dp2[l][r]) % p;

    cout << ans * pow2[n - 1] % p << '\n';
  }
}

First, since all sequences of choices have same probability to occur, we can turn it into a counting problem and divide the answer by the number of possibility, that is

where $$$ope_m$$$ represent the sequence of operation done to the array $$$b_n$$$($$$ope_i \in [1, n] \text{ }\forall i$$$).

At first glance, the problem seems to have too much stuff going on, so let's try to solve a more constrained version(invent subtasks) and see if we can generalize the solution back to the original problem later.

Subtask: $$$v = 1, a_i = 0 \text{ }\forall i \in [1, n]$$$, operations are point add rather than suffix add

Since constraints on $$$a_n$$$ and $$$v$$$ feel like a "noise" and not related to the core of the problem, also doing suffix add feels a bit annoying, let's get rid of them first. How can we solve this problem?

Assume we label element added at the $$$i$$$-th operation with $$$i$$$, then by the product trick, we can think of $$$\prod_\limits{i = 1}^n b_i$$$ as counting the number of ways to pick one element from each entry of sequence $$$b_n$$$, then we can further enumerate all possible choices of elements, that is

where $$$c_i$$$ represents the label of element chosen in $$$i$$$-th entry, and we only need to consider sequences satisfy $$$c_i \in [1, m] \text{ }\forall i, c_i \neq c_j \forall i \neq j$$$

Then using contribution to the sum trick (or swapping sigma/double counting...), we get

Which boils down to a simple combinatoric problem, for a fixed $$$c_n$$$, we can freely distribute elements not in $$$c_n$$$, and there are $$$\frac{m!}{(m-n)!}$$$ possible $$$c_n$$$ we need to consider, thus the answer will be

Now, let's lift the constraints one by one, trying to generalize the solution back to the original problem.

Subtask: $$$v = 1, a_i = 0 \text{ }\forall i \in [1, n]$$$

I decide to lift the suffix add constraint first because it feels more related to the core of the problem. How is this modification change our solution?

Since adding suffix $$$[i, n]$$$ should be equivalent to adding elements of same label to all entries in $$$[i, n]$$$, the condition $$$[\text{element }c_i\text{ belongs to i-th entry }\forall i]$$$ should be equivalent to $$$[ope_{c_i} \leq i \text{ }\forall i]$$$ rather than the above one, and it is possible to pick element of same label from different entries, thus condition for $$$c_n$$$ become just $$$c_i \in [1, m]$$$, so we can no longer assume the number of free elements is $$$m - n$$$. Which give us

Now the stuffs start to get complicated and can't be dealt with a simple formula, so instead of deriving a formula, let try to use the following DP to handle this.

About the transition, since we can let $$$c_{i + 1}$$$ be either an already appeared element or a new one, and if it is a new one, we should also determine the choice of respective operation, which have $$$(i + 1)$$$ possibility by the new condition we just stated above, so the transitions should be

and we consider the choices of free elements and permute elements in $$$c_n$$$ by multiplying some factor afterward, which gives us the answer

the original problem

Finally, let try to deal with constraint on $$$v$$$ and $$$a_n$$$, for $$$v$$$, the only change is that there are $$$v$$$ elements of same label added to a single entry rather then one element, thus we can choose $$$1$$$ elements out of $$$v$$$ elements from every entry. And for $$$a_n$$$, we can just let there be some extra elements before we do the operation, and when consider $$$i$$$-th slot, except choosing an element come from the operations, we can also choose the one already in the entry before the operations, which gives us the following transitions

and the final answer will be

After the long long thinking on the problem, all we need to do is to write a few line of code, which is amazing!

Conclusion

When solving this problem, I feel myself using a lot of techniques and problem solving skill I've ever learnt in my entire CP journey, and even I've known these stuffs for a fairly long time, I still got fascinated by the solution itself, especially the process of clarifying the core of the problem model by inventing proper subtasks, and the powerfulness of turning a counting problem into formula, which can lead further to the usage of some common techniques (product trick, contribution to the sum, DP, etc...)

Though I feel the whole solving path is a bit too long for me to solve it during contest, so if you have any shorter/smarter way to come up with the solution, please let me know by commenting below, I would be appreciated.

And finally, thanks for your reading and I hope this blog gives you some insights of problem solving :)

According to Cayley-Hamilton theorem, the power of a $$$n$$$ times $$$n$$$ matrix can be seen as a linear recurrence have atmost $$$n$$$ terms, so let say we have some $$$dp[n][m]$$$ which every $$$dp[i]$$$ is a $$$n$$$ times $$$1$$$ vector, and we can get $$$dp[i]$$$ from the previous $$$dp[j] (j < i)$$$ by multiplying a transition matrix $$$A_{n \times n}$$$, then we can manipulate Cayley-Hamilton theorem like below to get a linear recurrence of a certain entries of $$$dp[i]$$$, then brute-force the first $$$2n$$$ terms of $$$dp[i] (i \leq 2n)$$$, plug all of them into Berlekamp-Massey, and we will get the actual recurrence relation of a certain entries of $$$dp[i]$$$, finally compute the k-th term of linear recurrence in $$$O(n^2lgk)$$$ or $$$O(nlgnlgk)$$$ using FFT.

($$$A$$$ is a $$$n$$$ times $$$n$$$ matrix, $$$b_i$$$ is a $$$n$$$ times $$$1$$$ vector whose entry are all $$$0$$$ except i-th row is $$$1$$$)

Assume we will construct a palidrome $$$S$$$ of length $$$n + |s|$$$, then we can just build the left half of the string then the rest will be fixed.

To make sure $$$S$$$ contain $$$s$$$ as a subsequence, we can maintain two position $$$L, R$$$ which means $$$s[i](L \le i \le R)$$$ have not been inserted to string $$$S$$$, when we add a letter $$$X$$$ at the end of $$$S$$$, if $$$X = s[L]$$$, then we let $$$L$$$ become $$$L + 1$$$(because we already add $$$s[L]$$$ to $$$S$$$, if $$$X = s[R]$$$, then we let $$$R$$$ become $$$R - 1$$$.

So we can get the following dp solution.

$$$dp[i][L][R]$$$ store the number of string have length $$$i$$$, and $$$s[j](L \le j \le R)$$$ have not been inserted to the string. then we will have the following transition.

\begin{equation} dp[i][L][R] \mathrel{+}= \begin{cases} dp[i-1][L][R] & \text{if } L = R + 1 \text{ or } (s[L] \neq j \text{ and } s[R] \neq j)\\ dp[i-1][L-1][R] & \text{if } s[L-1] = j \text{ and } (s[R] \neq j \text{ or } L = R + 1)\\ dp[i-1][L][R + 1] & \text{if } s[R + 1] = j \text{ and } (s[L] \neq j \text{ or } L = R + 1)\\ dp[i-1][L-1][R + 1] & \text{if } s[L-1] = s[R + 1] = j \end{cases}
\end{equation}

time complexity: $$$O(26(n + |s|)|s|^2)$$$

#include<bits/stdc++.h>
//#define x() real()
//#define y() imag()
//#define int long long
//#define double long double
 
using namespace std;
 
using pii = pair<int, int>;
using pll = pair<long long, long long>;
//using Point = complex<double>;
//using Vector = complex<double>;
//using Segment = pair<Point, Point>;

/*
enum {
  NO_SOL,
  MULTI_SOL,
  ONE_SOL
};
*/
vector<pii> ans;
map<int, int> Plus, Minus;
int check(pii xBound, pii yBound) {
  if (Plus.size() > 1 or Minus.size() > 1) {
    return 0;
  }

  int pfir, mfir;
  if (Plus.size() == 1) {
    for(pii X : Plus)
      pfir = X.first;
  }
  if (Minus.size() == 1) {
    for(pii X : Minus)
      mfir = X.first;
  }

  if (Plus.size() == 1 and Minus.size() == 1) {
    int x = (pfir + mfir) / 2;
    int y = (pfir &mdash; mfir) / 2;
    if (x + y != pfir or x &mdash; y != mfir)
      return 0;

    if (xBound.first <= x and x < xBound.second and
        yBound.first <= y and y < yBound.second) {
      ans.emplace_back(make_pair(x, y));
      return 2;
    } else
      return 0;
  } else if (Plus.size() == 1) {
    int D1 = xBound.first + yBound.first;
    int D2 = (xBound.second &mdash; 1) + (yBound.second &mdash; 1);

    if (pfir == D1) {
      ans.emplace_back(make_pair(xBound.first, yBound.first));
      return 2;
    } else if (pfir == D2) {
      ans.emplace_back(make_pair(xBound.second - 1, yBound.second - 1));
      return 2;
    } else if (D1 < pfir and pfir < D2)
      return 1;
    else
      return 0;
  } else if (Minus.size() == 1) {
    int D1 = xBound.first &mdash; (yBound.second &mdash; 1);
    int D2 = (xBound.second &mdash; 1) &mdash; yBound.first;

    if (mfir == D1) {
      ans.emplace_back(make_pair(xBound.first, yBound.second - 1));
      return 2;
    } else if (mfir == D2) {
      ans.emplace_back(make_pair(xBound.second - 1, yBound.first));
      return 2;
    } else if (D1 < mfir and mfir < D2)
      return 1;
    else
      return 0;
  }

  return 3;
}

signed main() {
  ios::sync_with_stdio(false), cin.tie(NULL);

  int N; cin >> N;
  /*
  vector<vector<int> > vec(N, vector<int>(3));
  for(int i = 0; i < N; i++) {
    cin >> vec[i][0] >> vec[i][1] >> vec[i][2];
  }
  sort(vec.begin(), vec.end(), [](vector<int> a, vector<int> b) {
    if (a[1] == b[1])
      return a[0] == b[0] ? a[2] < b[2] : a[0] < b[0];
    else
      return a[1] < b[1];
  });
  */
  vector<pair<pii, int> > whyJudgeFail(N);
  for(int i = 0; i < N; i++)
    cin >> whyJudgeFail[i].first.second >> whyJudgeFail[i].first.first >>
           whyJudgeFail[i].second;
  sort(whyJudgeFail.begin(), whyJudgeFail.end());
  vector<vector<int> > vec(N, vector<int>(3, 0));
  for(int i = 0; i < N; i++) {
    vec[i][0] = whyJudgeFail[i].first.second;
    vec[i][1] = whyJudgeFail[i].first.first;
    vec[i][2] = whyJudgeFail[i].second;
  }

  vector<int> Xcor, Ycor;
  for(int i = 0; i < N; i++) {
    Xcor.emplace_back(vec[i][0]);
    Ycor.emplace_back(vec[i][1]);
  }
  Xcor.emplace_back(-1e7);
  Ycor.emplace_back(-1e7);
  Xcor.emplace_back(1e7);
  Ycor.emplace_back(1e7);
  sort(Xcor.begin(), Xcor.end());
  sort(Ycor.begin(), Ycor.end());
  N += 2;

  bool infSol = false;
  for(int i = 0; i < N &mdash; 1; i++) {
    Plus.clear();
    Minus.clear();
    pii xRange = make_pair(Xcor[i], Xcor[i + 1]); //[L, R)
    if (xRange.first == xRange.second)
      continue;
    for(vector<int> &VEC : vec) {
      if (VEC[0] <= xRange.first) {
        if (Minus.find(Minus[VEC[0] &mdash; VEC[1] + VEC[2]]) == Minus.end())
          Minus[VEC[0] &mdash; VEC[1] + VEC[2]] = 1;
        else
          Minus[VEC[0] &mdash; VEC[1] + VEC[2]] += 1;
      } else {
        if (Plus.find(VEC[0] + VEC[1] &mdash; VEC[2]) == Plus.end())
          Plus[VEC[0] + VEC[1] &mdash; VEC[2]] = 1;
        else
          Plus[VEC[0] + VEC[1] &mdash; VEC[2]] += 1;
      }
    }   

    int tmp = check(xRange, make_pair(Ycor[0], Ycor[1]));
    if (tmp == 1) 
      infSol = true;

    int idx = 0;
    for(int j = 1; j < N - 1; j++) {
      pii yRange = make_pair(Ycor[j], Ycor[j + 1]);
      if (yRange.first == yRange.second)
        continue;

      while(idx < vec.size() and vec[idx][1] <= Ycor[j]) {
        if (vec[idx][0] <= xRange.first) {
          int origin = vec[idx][0] - vec[idx][1] + vec[idx][2];
          if (--Minus[origin] == 0) 
            Minus.erase(origin);
          if (Plus.find(vec[idx][0] + vec[idx][1] + vec[idx][2]) == Plus.end())
            Plus[vec[idx][0] + vec[idx][1] + vec[idx][2]] = 1;
          else
            Plus[vec[idx][0] + vec[idx][1] + vec[idx][2]] += 1;
        } else {
          int origin = vec[idx][0] + vec[idx][1] - vec[idx][2];
          if (--Plus[origin] == 0)
            Plus.erase(origin);
          if (Minus.find(vec[idx][0] - vec[idx][1] - vec[idx][2]) == Minus.end())
            Minus[vec[idx][0] - vec[idx][1] - vec[idx][2]] = 1;
          else
            Minus[vec[idx][0] - vec[idx][1] - vec[idx][2]] += 1;
        }
        idx++;
      } 

      int tmp = check(xRange, yRange);
      if (tmp == 1)
        infSol = true;
    }
  }

  sort(ans.begin(), ans.end());
  ans.resize(unique(ans.begin(), ans.end()) &mdash; ans.begin());

  if (infSol or ans.size() > 1)
    cout << "uncertain\n";
  else if (ans.size() == 1) 
    cout << ans[0].first << ' ' << ans[0].second << '\n';
  else
    cout << "impossible\n";

  return 0;
}