Dynamic Programming
There were huge number of sources on the internet on this topic but still we (me and my friend) couldn't understand any of it for a very long time until we fiddled with code and tracked the output for every change in the input. So this repository is exactly created for people like us to make the transition from greedy to dynamic programming easier. This will just be an introduction to dynamic programming, so that one can pick it up from there. I have added additional sources for practice and other online tutorials that I found a little helpful at the end and will continue to do so as I find something new. It is for programmers who are comfortable with brute-force and might not the serve the purpose for absolute beginners. Contributions or suggestions are welcome.
Definition
So what's dynamic programming? Let's first look at a more formal definition.
Dynamic programming (also known as dynamic optimization) is a method for solving a complex problem by breaking it down into a collection of simpler subproblems, solving each of those subproblems just once, and storing their solutions. The next time the same subproblem occurs, instead of recomputing its solution, one simply looks up the previously computed solution, thereby saving computation time at the expense of a (hopefully) modest expenditure in storage space. (Each of the subproblem solutions is indexed in some way, typically based on the values of its input parameters, so as to facilitate its lookup)(Source-Wiki).
Or more simply, it is technique to save intermediate results in a calculation in any comfortable format so that the result can be used for further computation instead of calculating it all over again at the arrival of an additional input. Sounds simple enough? Yes, indeed it is, let's have a look at an example to put it right through our skull.
Before that, we need to identify whether a problem has the following properties, inorder to be solved by Dynamic Programming(DP)
Problems:
Minimum cost problem
Given a cost matrix cost[][] and a position (m, n) in cost[][], write a function that returns cost of minimum cost path to reach (m, n) from (0, 0). Each cell of the matrix represents a cost to traverse through that cell. Total cost of a path to reach (m, n) is sum of all the costs on that path (including both source and destination). You can only traverse down, right and diagonally lower cells from a given cell, i.e., from a given cell (i, j), cells (i+1, j), (i, j+1) and (i+1, j+1) can be traversed. You may assume that all costs are positive integers.
| 1 | 2 | 3 |
|---|---|---|
| 4 | 8 | 2 |
| 1 | 5 | 3 |
(forgive the highlighting of the first row it is of no special significance)
Solution:
Me: So how would you go on solving that? Friend: Oh, the properties I read talked about saving the sub-problems to make the computations easier! Me: What are the sub-problems here? Friend: Oh, it's too tough. Me: No, it's not we will work together.
How would you normally solve it, forgetting about code for a minute. You probably eye all the cells, adding the cost along the path till you reach the destination. But you don't know if it's minimum, so you start adding again by traversing in a different direction. Then maybe after considering all paths, you come up with a cost that's give you the least.
That's pretty much it.
My friend interrupts, Friend: But the above method only solves the problem for one particular destination, what if we want to calculate the total cost for reaching a different destination. Me: Good point! Friend: That's why we store the minimum cost for reaching each cell in the array from the first cell. That way when we fill up all cells we will be left with solutions of every cell. Friend: I lost you there. Me: Haha, let me finish.
So what do we know so far? — There's an array and we can move right, down and digonally lower. — We need to print the minimum cost of traversing to the given destination. — And we start at the first cell.
Breaking down the problem:
Me: What is simply the cost of moving from [0,0] to [0,1]? Friend: It's 2 + 1 = 3 Me: What is the minimum cost of moving from [0,0] to [0,1]? Friend: Still 3, because there's no other way we could reach [0,1] since we can only move right or down or diagonally lower. We can only reach [0,1] from [0,0]. Me: Excellent! So what is the minimum cost of moving from [0,1] to [0,2]? Friend: Oh wait, the cost of moving from [0,0] to [0,1] is 3, hence [0,1] to [0,2] would be 3 + cost of getting to (0,2) which is 3 + 3 = 6. Me: Now shall we store this obtained cost corresponding to each cell in a different array, so that we can return them, when the cell is the destination? Friend: Fair enough.
| Table A | Min cost |
|---|---|
| | 1 | 2 | 3 | |---|---|---| | 4 | 8 | 2 | | 1 | 5 | 3 | | | 1 | 3 | 6 | |---|---|---| | — | — | — | | — | — | — | |
Why not code it up too?
minarr[0][0] = a[0][0];
for(i=1;i<n;i++)
minarr[0][i] = minarr[0][i-1] + a[0][i];
where n is the number of rows
We transfer the first element as it is to the min cost table and calculate the cost of others in the row.
Friend: Why not the columns? The cells in the first column have only one way of reaching them too, which is down from the first cell. Me: Yeah absolutely, that's our next step.
Similarly, we calculate the cost of reaching each column by adding the cell with the previous ones in the column.
| Table A | Min cost |
|---|---|
| | 1 | 2 | 3 | |---|---|---| | 4 | 8 | 2 | | 1 | 5 | 3 | | | 1 | 3 | 6 | |---|---|---| | 5 | — | — | | 6 | — | — | |
We'll code that up too!
for(i=1;i<m;i++)
minarr[i][0] = minarr[i-1][0] + a[i][0];
where m is the number of columns
Friend: Now, how do we calculate the minimum cost to reach cell [1,1]? Me: We know we can only traverse left, down or diagonally lower cell. Hence we can reach cell [1,1] only from cell [0,0] or [0,1] or [1,0]. So now that our table already has the minimum values to reach [0,0], [0,1] and [1,0], simply the minimum of those three values plus the cost of reaching cell [1,1] gives us our result.
So the cost to reach cell [1,1] = a[1,1] + min(minarr[0,0], minarr[0,1], minarr[1,0]) minarr[1,1] = 8 + min(1,3,5) So, minarr[1,1] = 9
Similarly we do for all cells, starting from 1,1.
Let's code it up again,
for(i=1;i<n;i++)
for(j=1;j<m;j++)
minarr[i][j] = (a[i][j] + min(minarr[i-1][j-1],minarr[i][j-1],minarr[i-1][j]));
| Table A | Min cost | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
Now that our table is filled, we simply return the cell of the given destination in the minimum cost array. Here is a similar problem.
Hence by considering the elements one by one we have built up our solution or in DP terms we have acquired our solution in bottom up fashion(tabulation method) from the sub-problems. There's another approach to it called memoizatation. The difference between both is explained in the article over here.
Longest increasing subsequence
The Longest Increasing Subsequence (LIS) problem is to find the length of the longest subsequence of a given sequence such that all elements of the subsequence are sorted in increasing order. For example, the length of LIS for {10, 12, 32, 2, 22, 23, 25, 30} is 6 and LIS is {10, 12, 22, 23, 25, 30}
Solution:
How would go on solving this problem? What would you store to make the calculations easier? Okay simply, how would you solve the above problem using brute force just like how you would perform a selection sort!
| 10 | 12 | 32 | 2 | 22 | 23 | 25 | 30 |
|---|---|---|---|---|---|---|---|
| k,i | j |
Friend: I would compare every element with every other element, if it's greater than the current one, I would increase count variable and I would print the highest count, I get. Roughly I would code it something like this
pseudo code (It's okay if you don't understand my friend's code)
for(i=0;i<n-1;i++)
{
count = 1;
for(j=i+1,k=i;j<n,k<n-1;j++)
{
if(a[j] > a[k])
{
k=j;
count++;
}
if(count>maxi)
maxi = count;
}
}
printf("\nMax-length = %d\n",maxi);
Me: Let's run it. Friend: Uh? Okay. Me: So what's the output? Friend: The program returns, max-length = 5, which I guess is {2, 22, 23, 24, 25}. But we know it's 6 and the LIS is {10, 12, 22, 23, 25, 30}. Why does it fail to catch the above lis?
Me: Because while traversing {10, 12, 32, 22, 23, 25, 30} the code will run as follows,it will check, if(10>12) yes--> count is 2, then if(32>12) yes--> count is 3, then At this point count = 3, from there on count won't get incremented because the following elements are lesser than 32 and hence condition like (22>32) will consecutively fail.
Friend: If only it knew that by avoiding 32 and traversing through the rest of the array we would actually obtain the result which is max-length = 6. Me: This is exactly the information we store for our computation using DP. In brute force terms, we store the count variable for all possible alternatives of traversal in the array and then simply find the maximum of it(Note: Not that brute force cannot solve the problem, a different approach might but definitely in exponential time).
NOTE: And my friend has set count=1 and not 0 initially, because when we have a case where all numbers are same in the array i.e {2, 2, 2, 2}, we must return count as 1 since one element is the still a subarray of the larger one which is simply { 2 } therefore returning 0 would be wrong.
Dp solution:
Me: So how would you code the same in dp, well actually it's easier. Friend: Since you said we store counts of all variables, we initialize an array of same size of corresponding counts? Me: Exactly, we first start off by creating another array for storing the count for each member of the array as we discussed and initialize all of them to 1.
| array | 10 | 12 | 32 | 2 | 22 | 23 | 25 | 30 |
|---|---|---|---|---|---|---|---|---|
| count | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| j | i |
Friend: Now we check in a similar way? Me: Yeah but for now, lets us consider only the element 10 exists in the array. Friend: Why? Me: To make it simpler?! Why else? Listen along. So what is the longest increasing subsequence then? Friend: 1 of course and LIS is {10}. Me: So now, say, we add 12 and set it's initial count to 1
| array | 10 | 12 |
|---|---|---|
| count | 1 | 1 |
| j | i |
Friend: We check if(12>10) so 12's count gets incremented? Me: Yes, now that 12>10, 12's count becomes count of 10 + 1 since count of 10 already represents the longest increasing subsequence that can be made with the existing elements. Count of 12 now represents {10} + {12} = {10 ,12} or simply count[i] = count[j]+1; which is 2
Friend: So let me clear this up, when 10 was alone LIS is 1 and now that 12 is added and we find {10, 12} could be LIS since 12>10 and so we add count of 10's to 12's count and plus 1 to include the number itself. Me: That's right and the array becomes,
| array | 10 | 12 |
|---|---|---|
| count | 1 | 2 |
| j | i |
Now let us consider 32, increment i to 32 and j to 10 i.e. j to the starting element of the array and traverse from the beginning to see adding 32 provides a longer subsequence. The array becomes,
| array | 10 | 12 | 32 |
|---|---|---|---|
| count | 1 | 2 | 1 |
| j | i |
**Friend:** Yes, it does prove longer. Since (32>10) therefore we increment 32's count --> count[i] = count[j]+1;
Me: We check all numbers before 32 to see if they can be added to form a sequence with it, so increment j, continue filling in the boxes!
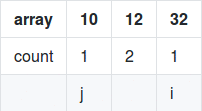
**Friend**: Okay I will, So if(32>12) --> 32's count = 12's count + 1 = (2+1) = 3
| array | 10 | 12 | 32 |
|---|---|---|---|
| count | 1 | 2 | 3 |
| j | i |
Similarly, considering element 2 the array becomes,
| array | 10 | 12 | 32 | 2 |
|---|---|---|---|---|
| count | 1 | 2 | 3 | 1 |
| j | i |
The array stays the same since each case checking if(2>10) , if(2>12) or if(2>32) fails, and it's count variable remains unchanged.
Now I'm adding the next number, 22 and check for 10, 12, 32, similar to the previous one, for 10 and 12, count of 22 is incremented to 3 and with 32 it fails and remains as 3, and j is incremented to point 2.
| array | 10 | 12 | 32 | 2 | 22 |
|---|---|---|---|---|---|
| count | 1 | 2 | 3 | 1 | 3 |
| j | i |
Now if(22 > 2) --> count of 22 becomes count[j]+1 i.e. 2? **Me:** Haha, glad you paused and asked, in short No, we know that count reflects the longest subsequence. By traversing other elements in the array, we obtained 3 as longest subsequence for 22. So why lower it to 2? Hence while adding count[i] = count[j]+1 make sure it benefits the cause. Therefore place count[i] = max(count[j]+1,count[i]) ie with the maximum of two numbers to avoid such cases.
And similarly the rest of the array is traversed and the array becomes,
| array | 10 | 12 | 32 | 2 | 22 | 23 | 25 | 30 |
|---|---|---|---|---|---|---|---|---|
| count | 1 | 2 | 3 | 1 | 3 | 4 | 5 | 6 |
| j | i |
Since the highest is 6, that gives the longest increasing subsequence, the video of the above traversal is linked here(different example). Let's have a look at the code snippet of the same below. As we have learnt, — We intialize count array to 1 — Then calculate count for every element
for(i=0;i<n;i++)
count[i] = 1;
for(i=1;i<n;i++)
{
for(j=0;j<i;j++)
{
if(array[i] > array[j])
count[i] = max(count[i],count[j]+1);
}
}
After that we find the maximum of the count array and print it.
More to come
- Minimum coin change
Points to remember
- Dynamic programming is just like any like any other kind you get some, you don't get some practice makes it all better. I have lot to do too.
- From my experience, it is similar to brute force but instead of exploring the whole input space, you find a way to store intermediate results that arise from the input and exhaustively explore that for the required result.
- Yes, it is indeed a method of trading space for time. A recursive approach may utilize a little less space but dynamic programming approach is quicker.
Other resources
- Hackerearth article explaining more on "Why dynamic programming"
- How to approach Dynamic Programming by Paul Baltescu on Quora
- Geeks for geeks tutorials
- Hackerearth article for problems involving grids
## Problems lists from various sites









