When finding the contribution of a straight line in a problem and seeking the maximum or minimum value, some targeted algorithms are usually used to solve it. If you find a contribution formula related to the straight line formula and need to find the maximum or minimum value among the contribution values, consider the following algorithms.

1. Li Chao Segment Tree

1. Algorithm Explanation

The Li Chao segment tree is a data structure for handling straight line problems derived from the segment tree. The operations it can handle are:

• Query the maximum or minimum value at a single point;
• Add a straight line to an interval.

We build a segment tree for the interval (a segment tree with dynamic node creation is more common). Each node stores only one straight line (slope + intercept). For a single-point query, we traverse the points on the path from the root to the leaf node corresponding to the subscript, calculate the results corresponding to the stored straight lines, and make contributions. For adding a straight line, first find the corresponding nodes on the segment tree for the interval where the straight line is located, and then update a single node to be updated according to the following operations:

• This node retains the straight line with the better value at the midpoint of the interval and passes the other straight line down.
• If the straight line to be passed down is better at the left boundary of the interval, it is used to update the left child.

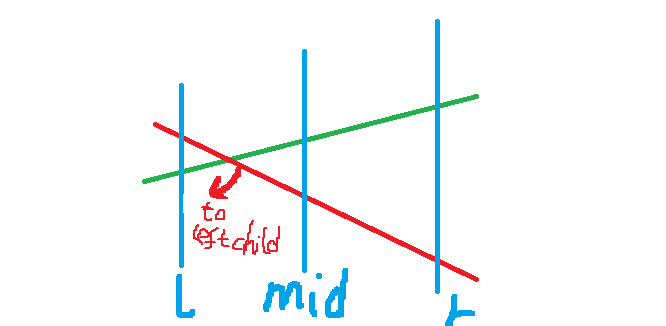
• If the straight line to be passed down is better at the right boundary of the interval, it is used to update the right child.

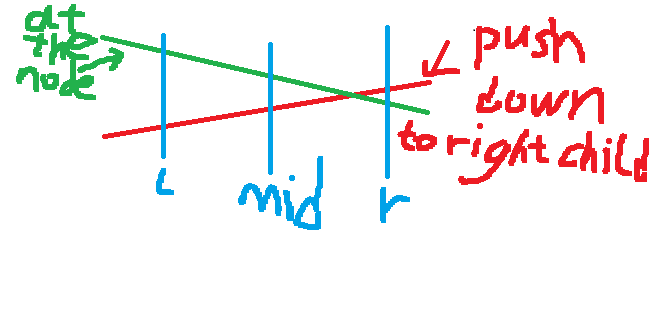
• If a vertically upward straight line appears, it is generally processed as a straight line with a slope of 0 and an intercept equal to the optimal point on the straight line.

It can be found that at most one of the operations in $$$2$$$ and $$$3$$$ will update the child. It can be concluded that the worst-case time complexity for a single-point update is $$$\operatorname{O}(\log_2 n)$$$. Any interval will correspond to $$$\operatorname{O}(\log_2 n)$$$ nodes, and the time complexity for adding a straight line to any interval is $$$\operatorname{O}(\log_2^2 n)$$$. However, when optimizing the straight line transfer, mostly only global addition is used, and only the root node needs to be updated, resulting in a time complexity of $$$\operatorname{O}(\log_2 n)$$$.

2. Advantages

• Easy to use: Optimizing the straight line transfer with the Li Chao segment tree does not require ensuring the monotonicity of the straight line slope. It is straightforward to apply in implementation and supports persistence, merging, and splitting of the segment tree. When the number of operations is limited, it can be brutally cleared, which is very useful.
• Code difficulty: The template of the Li Chao segment tree is similar to that of the segment tree. It is very simple for contestants who have mastered the segment tree proficiently. And the segment tree is a high-frequency knowledge point in competitions at the advanced level and above. Therefore, the code difficulty is not high for many contestants.
• Efficiency: Compared with the CDQ divide-and-conquer method, the Li Chao segment tree is in most cases $$$\operatorname{O}(\log_2 n)$$$ times faster in efficiency.

3. Limitations

Using the Li Chao segment tree requires ensuring that the number of points for which the optimal value is sought is limited when the straight line formula makes contributions, and it cannot support deletion.

4. Problem

CodeForces1179D

2. Monotonic Queue and Convex Hull

1. Algorithm Explanation

For the situation where the slopes of the straight lines added are monotonically non-deteriorating in the order of addition and the query coordinates are monotonically increasing, consider using a monotonic queue to obtain:

• When adding to the end of the queue, consider the magnitude of the abscissa of the intersection point of the added straight line and the last straight line and the abscissa of the intersection point of the last straight line and the previous straight line. If the former is smaller, delete the last straight line.
• If the contribution of the straight line at the head of the queue is worse than that of the next one, delete the head of the queue.

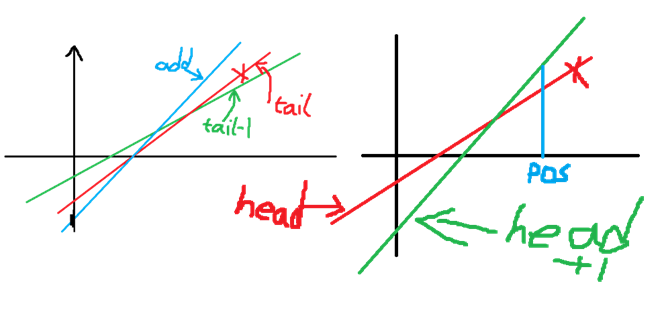
Operation $$$1$$$ is continuously performed before insertion until the last element does not meet the deletion condition. Operation $$$2$$$ is continuously performed before insertion until the head of the queue does not meet the addition condition. In this way, we obtain a linear solution for this type of straight line transfer problem. If we explain the problem in another way: - Insert nodes, and the abscissas are monotonically increasing; - Query the intercept of the straight line with the largest slope passing through one of the points.

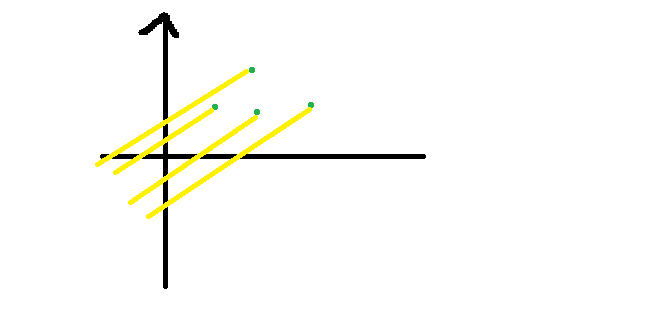
Then the solution is the convex hull. Also, maintain a double-ended queue. When inserting, delete the end of the queue when it is found to turn upward.

The two methods have different explanations but the same essence. You can choose according to your preference. For the situation where the query points are not necessarily monotonically increasing, consider not deleting the head of the queue and perform a binary search during the query, which will add an additional $$$\operatorname{O}(\log_2 n)$$$. For the situation where the slopes of the straight lines are not necessarily monotonically increasing, consider adding the CDQ divide-and-conquer method. Sort the left half according to the slope each time to update the right half, and the time complexity is $$$\operatorname{O}(n\log_2^2 n)$$$.

2.Advantages

• Code difficulty: The queue part is easy to write, and the CDQ divide-and-conquer is not difficult to write either;
• Efficiency: The insertion and deletion of the queue are amortized linearly.

3.Disadvantages

For the situation that requires the CDQ divide-and-conquer method, it needs to be offline, and it may be inconvenient to apply for complex problems.

4.Example Problem

SPOJ2940

3.Summary

Different algorithms have different advantages and disadvantages, and different algorithms should be used for different situations. In the problem of the maximum or minimum contribution of a straight line, we find that the Li Chao segment tree and the monotonic queue can help us solve this problem quickly and further handle more complex dynamic programming problems.

I'm calling MikeMirzayanov to solve that.

Here are some useful conclutions for naive algorithms to solve number theory problem,I hope you can know something about it and solve number theory problems more easily.

1.The number of prime factors of an integer

It's sure that the number of prime factors of an integer is very small,and an integer $$$v$$$ can be the product of at most $$$\log_2(v)$$$ primes ($$$2 ^ k$$$ the worst).This can be used for bruteforce and State compression.

Thanks AkiLotus to remind me that for the number of distinct prime factors of a integer $$$\operatorname{w}(n)$$$,$$$\sum_{i = 1}^n \operatorname{w}(n)$$$ is $$$\operatorname{O}(n \log \log n)$$$.

example:510D.

2.The number of factors of an integer

First of all,$$$\sum_{i = 1} ^ n \operatorname{d}(n) = \sum_{i = 1} ^ n [\frac{n}{i}] \approx n \ln n$$$.

Then I've found out that the number of factors of an integer($$$\operatorname{d}(n)$$$) is usually small,and to make sure,I made a code to get the maxinum number of the number of factors,and get:

1. For $$$n \le 10 ^ 4,\operatorname{d}(n) <= 64$$$;
2. For $$$n \le 5 \times 10 ^ 4,\operatorname{d}(n) <= 100$$$;
3. For $$$n \le 10 ^ 5,\operatorname{d}(n) <= 128$$$;
4. For $$$n \le 2 \times 10 ^ 5,\operatorname{d}(n) <= 160$$$;
5. For $$$n \le 3 \times 10 ^ 5,\operatorname{d}(n) <= 180$$$;
6. For $$$n \le 5 \times 10 ^ 5,\operatorname{d}(n) <= 200$$$;
7. For $$$n \le 10 ^ 6,\operatorname{d}(n) <= 240$$$;
8. For $$$n \le 5 \times 10 ^ 6,\operatorname{d}(n) <= 384$$$;
9. For $$$n \le 10 ^ 7,\operatorname{d}(n) <= 448$$$;

So if your solution of a problem is $$$\operatorname{O}(n\max \operatorname{d}(a_i))$$$ or $$$\operatorname{O}(\sum \operatorname{d}(a_i))$$$,it might be correct because for $$$a_i \le 10 ^ 7$$$,it's sure that $$$\operatorname{d}(a_i) \le 500$$$.

examples:

• 1780F
• 990G
• 645F

3.Euler's Function: $$$\operatorname{O}(\log_2 n)$$$ times to $$$1$$$.

It's sure that $$$\phi(n) \le \frac{n}{2}$$$ for $$$2 | n$$$,and $$$2 | \phi(n)$$$ for $$$n > 1$$$.So if you use operation $$$x = \phi(x)$$$ for $$$x = n$$$ initially,it will become $$$1$$$ in $$$\operatorname{O}(\log_2 n)$$$ times.

In fact,it can be related to problems about power,when we try to solve the problem using Euler's Theorem or Extend Euler's Theorem.

example:

• 906D
• 1797E

4.Prefixes: $$$\operatorname{O}(\log_2 n)$$$ distinct prefix great common diverse/and/or

Thanks Ghulam_Junaid and Timosh to remind me about the feature.

For $$$\gcd(a_1,a_2,...,a_k)$$$,We can add a new integer $$$a_{k + 1}$$$ and found:

• If $$$\gcd(a_1,a_2,...,a_k) | a_{k + 1}$$$,it's sure that $$$\gcd(a_1,a_2,...,a_k,a_{k + 1}) = \gcd(a_1,a_2,...,a_k)$$$.
• Otherwise,$$$\gcd(a_1,a_2,...,a_k,a_{k + 1}) \le [\frac{\gcd(a_1,a_2,...,a_k)}{2}]$$$.

So there are at most $$$\log_2 n$$$ distinct prefix great common diverse.

For operator and or or,every integers can be written by $$$\log_2 n$$$ digits,and:

• For operator and,the number of "1" in the digits decreases;
• And for operator or,the numbr of "1" increases;

So there are at most $$$\log_2 n$$$ prefixes and suffixes.

example:

• 475D
• 1139D
• 2005D
• 2013E

5.At most $$$[2\sqrt{n}]$$$ distinct integers of $$$[\frac{n}{i}],1 \le i \le n$$$.

Known as number theory chunking in public,we can proof that $$$[\frac{n}{i}] = [\frac{n}{[\frac{n}{i}]}]$$$,and then split $$$[1,n]$$$ to $$$\operatorname{O}(\sqrt n)$$$ sections like $$$[l,r = [\frac{n}{l}]]$$$,it's really useful while calculating $$$\sum_{i = 1}^n \operatorname{f}([\frac{n}{i}])$$$ or it's easy to consider several integer $$$v_1,v_2,...,v_k$$$ together when $$$[\frac{n}{v_i}],1 \le i \le k$$$ is the same.

If we use Möbius inversion first,we might found that we have to calculate $$$\operatorname{f}(\frac{x}{d})$$$,using the feature we can found out that we can calculate the function just $$$[2\sqrt{n}]$$$ times for distinct numbers.

example:

• ARC060B in AtCoder
• 1082 in CSES
• P1829 in Luogu
• P3327 in Luogu
• 538F

Last:written in the end:

I would like to thank:

• OtterZ who edit the blog;
• AkiLotus,PeruvianCartel,peltorator for correcting the mistake;
• Ghulam_Junaid to remind me about a feature about great common diverse;
• Timosh to remind me about a feature about operator and and or.
• AkiLotus to remind me something about prime factors.
• Timosh,The-Winner,swarup19 to provide some examples.

There are some bugs and features exists while compiling a c++ code,it looks weird but really exists on standard c++ compiler.I'll write down the bugs and features here to remind you to aware of them.

1.stl::vector:fail to use operator "=".

I was trying to implent the merge function of segment tree while solving the task,and the initial code is

int mrg(int x,int y,int l,int r){
	if(x == -1 || y == -1)
		return x + y + 1;
	int u = sum.size();
	sum.push_back(sum[x] + sum[y]);
	lc.push_back(-1);
	rc.push_back(-1);
	if(l == r)
		return u;
	int m = (l + r) >> 1;
	lc[u] = mrg(lc[x],lc[y],l,m);
	rc[u] = mrg(rc[x],rc[y],m + 1,r);
	return u;
}

and found that it will get WA on test #6 using the language C++14(GCC 6-32).Then I found out that the

lc[u] = mrg(lc[x],lc[y],l,m);
rc[u] = mrg(rc[x],rc[y],m + 1,r);

might got wrong.That because the location of lc[u] changed after using lc.push_back() and the same as rc[u],so the operator "=" might not work.

The bug have been fixed since C++17(GCC 7-32),but if you compile your code using language C++ and the previous version before C++17(GCC 7-32),the bug still exists.

2.vector:Can vector be compiled by head file ?

I've participated on a school contest and found that a code with stl :: vector ran successfully without head file <vector>,after that,I made some testing and found something miraculous:

If the compiler is on Windows system (on codeforces,Dev c++ on Windows,etc),you can use <algorithm> instead of <vector> to compile stl :: vector,but if the compiler is on Linux system (Luogu,and so on),<algorithm> is unable to compile stl :: vector.Also, in Windows <iostream> is able to compile stl :: vector and it's invalid to use <iostream> to compile stl :: vector in Linux.So,for participants,especially for Chinese who is willing to engage on Olympics in informatics,please be aware of this.

For more such bugs and features,you can reply to the comment and I'll put some of them that sometimes exists but not well-known here.

1.Introduction

Binary grouping is a way to implent dynamic insertion.If you found that the query for a data structure constructed by inserted elements from set $$$s$$$ can be answered online and be solved by uniting querys from a set of data structures built on a partition of $$$S$$$ in $$$O(h(n,m))$$$ as $$$m$$$ is the number of subsets in the partition and you can construct a data structure in $$$O(\operatorname{f}(n))$$$,It means that you can divide the elements in groups,for $$$n = \sum 2 ^ {a_i}(a_i > a_{i + 1})$$$,We can divide $$$n$$$ elements into groups,each group has $$$2^{a_k}$$$ elements,in this way we divided elements to $$$\log_2{n}$$$ groups.Then we build a data structure for each group of insertions using the construct algorithm.

When we insert a new element,we divide it in a group,and when we found a group that its size is the same as the new group,we merge the two groups into one group and rebuild a data structure with the elements in the group.Using the method,we get a way to implent dynamic insertion and the method to construct is $$$O(\sum {f(x)})(\sum x = n \log_2 n) \approx O(f(n)\log_2 n)$$$ in total and $$$O(h(n,\log_2 n))$$$ for each query.

2.Examples

It can be used for kd-tree,but I haven't found an example on the site,so please leave a comment if you found the example.

The example of using the method on kd-tree is P4148 on luogu,in the problem,the elements is the points in the first operation and we can use kd-tree to deal with the elements and answer the query online.But we have to implent dynamic insertion,so we use this method.

#include<algorithm>
#include<cstdio>
using namespace std;
namespace K_D_tree{
	const int N = 300009,K = 2;
	int V = 0;
	struct node{
		int p[K],mx[K],mn[K],lc,rc,sz,sum,val;
	}a[N];
	int sro;
	int build(int l,int r,int nk,node a[]){
		if(l > r)
			return 0;
		if(l == r){
			for(int i = 0; i < K; i ++){
				a[l].mx[i] = a[l].p[i];
				a[l].mn[i] = a[l].p[i];
			}
			a[l].sz = 1;
			a[l].sum = a[l].val;
			return l;
		}
		int m = (l + r) >> 1;
		sro = nk;
		nth_element(a + l,a + m,a + r + 1,[](node x,node y){return x.p[sro] < y.p[sro];});
		a[m].lc = build(l,m - 1,(nk + 1) % K,a);
		a[m].rc = build(m + 1,r,(nk + 1) % K,a);
		for(int i = 0; i < K; i ++){
			a[m].mx[i] = max(a[m].p[i],max(a[a[m].lc].mx[i],a[a[m].rc].mx[i]));
			a[m].mn[i] = min(a[m].p[i],min(a[a[m].lc].mn[i],a[a[m].rc].mn[i]));
		}
		a[m].sz = r - l + 1;
		a[m].sum = a[a[m].lc].sum + a[a[m].rc].sum + a[m].val;
		return m;
	}
	int fnd(int k,int q[]){
	    if(k == 0)
	        return 0;
		for(int i = 0; i < K; i ++){
			if(q[i] > a[k].mx[i] || q[i] < a[k].mn[i])
				return 0;
		}
		bool flg = true;
		for(int i = 0; i < K; i ++){
			if(q[i] != a[k].p[i]){
				flg = false;
				break;
			}
		}
		if(flg)
			return k;
		else 
			return max(fnd(a[k].lc,q),fnd(a[k].rc,q));
	}
	void change(int k,int q[],int ad){
	    if(k == 0)
	        return ;
		for(int i = 0; i < K; i ++){
			if(q[i] > a[k].mx[i] || q[i] < a[k].mn[i])
				return ;
		}
		bool flg = true;
		for(int i = 0; i < K; i ++){
			if(q[i] != a[k].p[i]){
				flg = false;
				break;
			}
		}
		if(flg){
			a[k].val += ad;
			a[k].sum += ad;
			return;
		}
		else {
			change(a[k].lc,q,ad),change(a[k].rc,q,ad);
			a[k].sum = a[a[k].lc].sum + a[a[k].rc].sum + a[k].val;
		}
	}
	int query(int k,int l[],int r[]){
		if(k == 0)
		    return 0;
		for(int i = 0; i < K; i ++){
			if(l[i] > a[k].mx[i] || r[i] < a[k].mn[i])
				return 0;
		}
		bool flg = true;
		int ret = 0;
		for(int i = 0; i < K; i ++){
			if(l[i] > a[k].p[i] || r[i] < a[k].p[i]){
				flg = false;
				break;
			}
		}
		if(flg)
			ret += a[k].val;
		flg = true;
		for(int i = 0; i < K; i ++){
			if(l[i] > a[k].mn[i] || r[i] < a[k].mx[i]){
				flg = false;
				break;
			}
		}
		if(flg)
			return a[k].sum;
		else 
			return ret + query(a[k].lc,l,r) + query(a[k].rc,l,r);
	}
	int str[100009],top = 0,lf[100009],rt[100009];
};
using namespace K_D_tree;
int lans,c,o,lp[K],rp[K];
int main(){
	scanf("%*d");
	while(true){
		scanf("%d",&o);
		if(o == 1){
			scanf("%d %d %d",&lp[0],&lp[1],&c);
			lp[0] ^= lans;
			lp[1] ^= lans;
			c ^= lans;
			bool flg = false;
			for(int j = 1; j <= top; j ++){
				if(fnd(str[j],lp) != 0){
					change(str[j],lp,c);
					flg = true;
					break;
				}
			}
			if(!flg){
				V ++;
				for(int j = 0; j < K; j ++){
					a[V].mx[j] = a[V].mn[j] = a[V].p[j] = lp[j];
				}
				a[V].sum = a[V].val = c;
				a[V].sz = 1;
				int u = 1,nlf = V;
				while(a[str[top]].sz == u){
					//printf("%d\n",top);
					nlf = lf[top];
					u = (u << 1);
					top --;
				}
				top ++;
				str[top] = build(nlf,V,0,a);
				lf[top] = nlf;
			}
		}
		else if(o == 2){
			scanf("%d %d %d %d",&lp[0],&lp[1],&rp[0],&rp[1]);
			lp[0] ^= lans;
			lp[1] ^= lans;
			rp[0] ^= lans;
			rp[1] ^= lans;
			//printf("%d %d %d %d\n",lp[0],lp[1],rp[0],rp[1]);
			lans = 0;
			for(int j = 1; j <= top; j ++){
				lans += query(str[j],lp,rp);
			}
			printf("%d\n",lans);
		}
		else{
			break;
		}
	}
	return 0;
}

In CF710F,we use the method on AC-Automation.In the task,we use a group to deal with the inserted string and an another group for deleted strings.In both of the groups,we devide the strings into groups and deal with insertions using the method and make ACAM for each group. When we insert a string,we insert it to the group of inserted strings and insert it to the group of deleted string when we delete it.For querys,if $$$x_i$$$ means that How many string is concluded if we arrive index $$$i$$$ while running the ACAM,$$$y_i$$$ is how many string ends here in the trie,we get $$$x_i = y_i + x_{fail_i}$$$,and the way to get answer is:

1. Run all the ACAMs in the group of inserted strings and add $$$x_i$$$ to answer while arriving index $$$i$$$.
2. Run all the ACAMs in the group of deleted strings and minus answer by $$$x_i$$$ while arriving index $$$i$$$.

Here is the Accepted submission.

written at the end of the blog

We would like to thank:

1. Masters who invent the method;
2. OtterZ edit the blog;
3. negative-xp to give advice and make the blog better.
4. adamant suggest a good problem as an example of using the trick.