Motivation

I saw that many beginners don't really understand how to compute complexity and make lots of mistakes in calculations of it. Even skilled programmers sometimes can make mistakes calculating complexity. I will describe a more intuitive way of how to understand the time and memory complexities, this will be the main focus of this blog. I will also include a more formal variant in the spoiler.

What is complexity

In simple words, complexity is just number of operations that the program make. For example, if you have a cycle from 1 to 1000 with step 1, it is 1000 operations and if there you make one addition and one multiplication, it is already 3000 (since you make this two operations 1000 times). For memory it works in the same way. If you make an array of 100 elements, it has memory complexity 100. But in fact, it is hard to calculate complexities up to 1 in general case, while it is also not really needed, since compute makes 1 operation really fast. In the same way, 10 operations or 1000 operations. In fact, when we calculate complexities we do not look at constant. It means, that n operations (where n is some variable and has some numeric value) same as 2*n operations, or n+100 operations is same as n operations. That is same as when we made 1647859 operation, we can just say that we made $$$10^6$$$ operations which is more easier to work with. The reason for it is that it is easier to calculate complexities, since you do not need to look for each operation. Also, since programs use variables which have some range, we will use variables as well.

Types of compexities

• $$$O$$$. This notation is used when we want to tell that our program make at most this complexity. It means, that if your program have one loop which takes n operations, it has complexity $$$O(n)$$$, but also has complexity $$$O(n^2)$$$. So, if we say that real number of operations that program makes will be a and number of operations that complexity says is b, then $$$a\le b$$$.

• $$$o$$$. This notation is used when we want to tell that our program make less then this complexity. It means, that if your program have one loop which takes n operations, it can have complexity $$$o(n^2)$$$, but also can have complexity $$$O(n^9)$$$. So, if we say that real number of operations that program makes will be a and number of operations that complexity says is b, then $$$a<b$$$.

• $$$\Theta$$$. This notation is used when we want to tell that our program make same number of operations as this complexity. It means, that if your program have one loop which takes n operations, it has complexity $$$\Theta (n)$$$. So, if we say that real number of operations that program makes will be a and number of operations that complexity says is b, then $$$a=b$$$.

• $$$\Omega$$$. This notation is used when we want to tell that our program make at least the same number of operations as complexity. It means, that if your program have one loop which takes n operations, it has complexity $$$\Omega (n)$$$ or it is also $$$\Omega (1)$$$. So, if we say that real number of operations that program makes will be a and number of operations that complexity says is b, then $$$a\ge b$$$.

• $$$\omega$$$. This notation is used when we want to tell that our program make more operations then complexity. It means, that if your program have one loop which takes n operations, it has complexity $$$\omega (1)$$$ or it is also $$$\omega (log(n))$$$, but not $$$\omega(n)$$$. So, if we say that real number of operations that program makes will be a and number of operations that complexity says is b, then $$$a> b$$$.

In the remaining blog I will use only big O notation, since it is, in my opinion, the most important and popular.

Evaluating complexities

There are some rules for evaluating complexities and here are some of them:

• $$$O(C)=O(1)$$$ for constant C and variables x and y.

• $$$O(x)+O(C)=O(x)$$$ for constant C and variables x and y.

• $$$O(x)+O(y)=O(x+y)=O(max(x,y))$$$ for variables x and y.

• $$$O(x)\cdot O(y)=O(x\cdot y)$$$ for variables x and y.

• $$$O(x)+O(x)=O(x)$$$ for variable x.

1.  #include <bits/stdc++.h>
2.  using namespace std;
3.  
4.  int main(){
5.      int n,k;
6.      cin>>n>>k;
7.      int a[n];
8.      for(int i=0;i<n;i++){
9.          cin>>a[i];
10.     }
11.     for(int i=n-k;i<n;i++){
12.         cout<<a[i]<<" ";
13.     }
14.     return 0;
15. }

1.      O(1)
2.      O(1)
3.  
4.      O(1)
5.      O(1)
6.      O(1)
7.      O(n)
8-10.   O(n)
11-13.  O(k)
14.     
15.     

1.  #include <bits/stdc++.h>
2.  using namespace std;
3.
4.  int main(){
5.      int n,m;
6.      cin>>n>>m;
7.      for(int i=0;i<x;i++){
8.          for(int j=0;j<y;j++){
9.              cout<<i+j<<endl;
10.         }
11.     }
12.     return 0;
13. }

1.  #include <bits/stdc++.h>
2.  using namespace std;
3.
4.  int main(){
5.      int n;
6.      cin>>n;
7.      int a[n+1]={0};
8.      for(int i=1;i<=n;i++){
9.          for(int j=i;j<=n;j+=i){
10.             a[j]++;
11.         }
12.     }
13.     for(int i=1;i<n;i++){
14.         cout<<a[i]<<" ";
15.     }
16.     return 0;
17. }

As we see, computing complexity is same as just solving some math inequality. This is why we need to memorize some cases like harmonic series, to not have wrong thoughts about the complexity.

More advanced examples

There is popular algorithm named divide and conquerer. Using this algorithm, it is hard to analyze the code complexity. For example,

#include <bits/stdc++.h>
using namespace std;

int a[100];

int find(int l,int r,int k){
    if(l+1==r){
        return a[l];
    }
    int m=(l+r)/2;
    if(a[m]>k){
        return find(l,m,k);
    }
    else{
        return find(m,r,k);
    }
}

int main(){
    int n,k;
    cin>>n>>k;
    for(int i=0;i<n;i++){
        cin>>a[i];
    }
    cout<<find(0,n,k);
    return 0;
}

One can note that it is just binary search algorithm. But in case we would not have if condition but go recursevily into both find fuunction, it seams that algorithm will work with really big complexity, but in fact it will work in $$$O(n)$$$. To analyze this code, we need additional notation. It is, $$$T(n)$$$. Really similar to $$$O(n)$$$ and in fact it is the same. It is needed to not have confusion when solving recursive time complexities. For example, we can denote first find function calling (from main) that it is $$$T(n)$$$, since we are looking for a value on $$$n$$$ other values. Then, we make number of values half of the number it was and just one additional operation to know which value to go. So, $$$T(n)=T(\frac{n}{2})+c$$$. Here, c is some constant. We will use it but not $$$O(1)$$$ and we will see why in a second. We can try to solve this just by iterating recursion. What I mean is that if $$$T(n)=T(\frac{n}{2})+c$$$, then $$$T(\frac{n}{2})=T(\frac{n}{4})+c$$$ so $$$T(n)=T(\frac{n}{4})+2\cdot c$$$. Using this, we can see that we can performe such operation $$$log(n)$$$ times, so $$$T(n)=T(\frac{n}{2^{log(n)}})+log(n)\cdot c$$$ and since $$$T(1)=1$$$, $$$T(n)=log(n)\cdot c=O(log(n))$$$. Here is why we used constant but not $$$O(1)$$$. It is because when we apply recursion, we get $$$2\cdot c$$$, which is also $$$O(1)$$$. In other words, it would be the same mistake as it was in the third example of previous section. Now, let's look at this code:

#include <bits/stdc++.h>
using namespace std;

int a[100];

int find(int l,int r){
    if(l+1==r){
        return a[l];
    }
    int m=(l+r)/2;
    return find(l,m)+find(m,r);
}

int main(){
    int n;
    cin>>n;
    for(int i=0;i<n;i++){
        cin>>a[i];
    }
    cout<<find(0,n);
    return 0;
}

One can see that it just finds sum of whole array, so it is working linearly, i.e. $$$O(n)$$$, but we will get to it. So, here $$$T(n)=2\cdot T(\frac{n}{2})+c$$$ since we also make constant number of operations but go in recurssions two times but not 1 as in previous example. Also note, that $$$T(1)=1$$$ since if there is only 1 element we return it. So, if we apply recusion $$$T(n)=2\cdot T(\frac{n}{2})+c=4\cdot T(\frac{n}{4})+2\cdot c=2^x\cdot T(\frac{n}{2^x})+x\cdot c$$$. We end our recurssion when $$$n=1$$$, i.e. $$$x=log(n)$$$, so $$$T(n)=n+log(n)\cdot c=O(n)$$$. So, it works in linear time. We can also say that each element was checked one time and since number of elements is linear, code also works linear. This intuition is good enough, but sometimes it can be bad.

Here are some tasks for you if you want to practice with it:

Also, there exists Master theorem, which basicly solve some instances of the problem. There are not all of them, but in practice that is enough. Also, there is geeralization of it which is almost useless in practice, hard to understand but cool in some sence. So, here is master theorem. It is solving all recurences which looks like this: $$$T(n)=a\cdot T(\frac{n}{b})+c\cdot n^d$$$ for any a, b, d. Let's denote $$$p=\frac{a}{b^d}$$$. Then, it just looks at three cases:

• $$$p<1$$$: $$$T(n)=O(n^d)$$$.

• $$$p=1$$$: $$$T(n)=O(n^d\cdot log(n))$$$

• $$$p>1$$$: $$$T(n)=O(n^{log_{b}a})$$$

In fact, it is just cases of the recursion technique we used, so if you don't know this theorem, you can solve it (and even more types of equations) using recursion technique.

Another cases

By now, we have talked only about precise algorithms, while in CP it is normal to use random or some tricks that make it hard to evaluate time complexity. For example, what if we write binary search, but we will choose random element but not middle.

#include <bits/stdc++.h>
using namespace std;

int main(){
    int n,k;
    cin>>n>>k;
    int a[n];
    for(int i=0;i<n;i++){
        cin>>a[i];
    }
    int l=0,r=n;
    while(l<r){
        int m=rand()%(r-l)+l;
        if(a[m]<k){
            l=m+1;
        }
        else{
            r=m;
        }
    }
    cout<<l<<endl;
    return 0;
}

Here talking about bit O notation is not correct, since number of operations depends on random. It is true that we can say here that code is working in $$$O(n)$$$ and we will be right since $$$log(n)\in O(n)$$$ and $$$n\in O(n)$$$ for example. But in cases when it is optimal to use random, we need it to be faster then trivial bound and in general in such cases data generated randomly depending on the way random is using. So, it is better to look at expectation value. So, let's denote $$$T(n)$$$ as complexity for $$$n$$$ elements. $$$T(n)=\frac{1}{n}(T(1)+T(2)+\dots+T(n))+1$$$ since probability of choosing $$$l+i$$$ point and cut segment to length i using this is $$$\frac{1}{n}$$$. So, $$$n\cdot T(n)=\sum_{i=1}^n T(i)+n$$$. Also, $$$(n-1)\cdot T(n-1)=\sum_{i=1}^{n-1}T(i)+n-1$$$. Hence, $$$n\cdot T(n)-(n-1)\cdot T(n-1)=T(n)+1$$$ which imply that $$$T(n)=T(n-1)+\frac{1}{n-1}=T(n-2)+\frac{1}{n-2}+\frac{1}{n-1}=...=\sum_{i=1}^{n-1}\frac{1}{i}$$$ which is harmonic series. So, this algorithm work in $$$O(log(n))$$$ in average which means that in general it will work like this, but sometimes when you are unlucky it can work longer or if you lucky it can work faster. But in fact, when it is used on practice in a right way it will work with complexity of expectation value.

How to use it

One GM can say how long code will work on codeforces just by looking at it. It can be with 50 ms error, but it is insane already, but how it can be. Assume that we have a code which has complexity $$$O(n)$$$ when $$$n$$$ is up to $$$10^7$$$ you can say that it will work in 1 sec. In fact, it can be 2 sec if constants are really big but it can be also less then a second in opposite case, but it is enough to assume that it will work in 1 sec. Also, it depens on the language you are making code. For example, code in Python will be much slower then in C. But it only partialy tell us how some GM can get the time with so good approximation. In fact, time depens not only on the number of iterations. It is known that + working faster then modulo or / operations but + on one computer can work faster then on other. It is like if you take some old computer then it will take much more time then for the computer that was made yesterday. So, it really depens on the computer, how it is compiling and the code itself. We cannot proccess all this, because it is too much of calculation but we can approximate it intuitevly. So the more you look at it, the better you are at this. But, it should be obvious that $$$O(\sqrt{n})$$$ will be longer then 1 sec for $$$n$$$ up to $$$10^{18}$$$ or that $$$O(log(n))$$$ for same n will work really fast.

Multitest

There is tricky part about multitests. It seems like if you solve one test in $$$O(n)$$$ and there are t tests then solution will work in $$$O(n\cdot t)$$$ which is right but some task include such line "The sum of $$$n$$$ over all test cases is $$$10^5$$$" or something like this. In fact, it is important. Assume that you solved task in $$$O(n)$$$ and n is up to $$$10^5$$$ but $$$t$$$ is up to $$$10^5$$$ also. Then, as you said solution $$$O(n\cdot t)$$$ will make $$$10^{10}$$$ operations at most which is slow in most cases. But if there is a line that sum of all $$$n$$$ is up to $$$10^5$$$, then it you can assume that your solution works in $$$O(n)$$$. Also, there can be that $$$n$$$ is up to $$$10^5$$$ but sum is up to $$$10^6$$$. Here, $$$O(n)$$$ is not really the case. In fact, the first case and this is just $$$O(\sum_{i=1}^{t}n_i)$$$ where $$$n_i$$$ is just time complexity of solution for test $$$i$$$. Then, if sum is up to $$$10^6$$$, your program will make $$$10^6$$$ operation. So, in such tasks $$$O(n\cdot \sqrt{n})$$$ is not a good decision even when $$$n$$$ is up to $$$10^4$$$ but sum is up to $$$10^6$$$ (you can use math and get better approximation in cases like $$$O(n\cdot \sqrt{n})$$$ or other. So it is better to try some solution which may get TLE).

2008A - Sakurako's Exam

#include <bits/stdc++.h>

using namespace std;

int main(){
    int t;
    cin>>t;
    while(t--)
    {
        int cnt1,cnt2;
        cin>>cnt1>>cnt2;
        if(cnt1%2)
        {
            cout<<"NO"<<endl;
        }
        else
        {
            if(cnt2%2==0)
            {
                cout<<"YES"<<endl;
            }
            else
            {
                if(cnt1==0)
                {
                    cout<<"NO"<<endl;
                }
                else
                {
                    cout<<"YES"<<endl;
                }
            }
        }
    }
}

t=int(input())
for _ in range(t):
    a,b=map(int,input().split())
    if a%2==1:
        print("NO")
        continue
    if a==0 and b%2==1:
        print("NO")
        continue
    print("YES")

2008B - Square or Not

#include <bits/stdc++.h>
using namespace std;

int main() {
    int t;
    cin>>t;
    while(t--)
    {
        int n;
        cin>>n;
        string s;
        cin>>s;
        int id=0;
        while(id<n&&s[id]=='1')
        {
            id++;
        }
        if(id==n)
        {
            if(n==4)
            {
                cout<<"Yes"<<endl;
            }
            else
            {
                cout<<"No"<<endl;
            }
        }
        else
        {
            if((id-1)*(id-1)==n)
            {
                cout<<"Yes"<<endl;
            }
            else
            {
                cout<<"No"<<endl;
            }
        }
    }
    return 0;
}

for _ in range(int(input())):
    n=int(input())
    s=input()
    i=0
    while i<n and s[i]=='1':
        i+=1
    if i==n:
        if n==4:
            print("Yes")
        else:
            print("No")
        continue
    i-=1
    if i*i==n:
        print("Yes")
    else:
        print("No")

2008C - Longest Good Array

#include <bits/stdc++.h>

using namespace std;

int main(){
    int t;
    cin>>t;
    while(t--)
    {
        long long a,b;
        cin>>a>>b;
        b-=a;
        long long l=2,r=1000000000;
        while(l<r)
        {
            long long m=(l+r)/2;
            if(m*(m-1)/2<=b)
            {
                l=m+1;
            }
            else
            {
                r=m;
            }
        }
        cout<<l-1<<endl;
    }
}

for _ in range(int(input())): 
    a, b = map(int, input().split())
    i = 0
    while a + i <= b:
        a += i
        i += 1
    print(i)

2008D - Sakurako's Hobby

#include <bits/stdc++.h>

using namespace std;

int main(){
    int t;
    cin>>t;
    while(t--)
    {
        long long n;
        cin>>n;
        long long p[n+1]={0},b[n+1]={0};
        int us[n+1]={0};
        for(int i=1;i<=n;i++)
        {
            cin>>p[i];
        }
        string s;
        cin >> s;
        for(int i=1;i<=n;i++)
        {
            if(us[i])continue;
            int sz=0;
            while(!us[i])
            {
                us[i]=1;
                sz += s[i - 1] == '0';
                i=p[i];
            }
            while(us[i]!=2)
            {
                b[i]=sz;
                us[i]=2;
                i=p[i];
            }
        }
        for(int i=1;i<=n;i++)
        {
            cout<<b[i]<<" ";
        }
        cout<<endl;
    }
}

t = int(input())
for _ in range(t):
    n = int(input())
    b = [0] * (n + 1)
    us = [0] * (n + 1)
    p = [k-1 for k in map(int, input().split())]
    s = input()
    for i in range(0, n):
        if us[i]:
            continue
        sz = 0
        while not us[i]:
            us[i] = 1
            sz += s[i] == '0'
            i = p[i]
        while us[i] != 2:
            b[i] = sz
            us[i] = 2
            i = p[i]
    print(" ".join(map(str, b[:-1])))

2008E - Alternating String

#include <bits/stdc++.h>

using namespace std;

int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        int n;
        cin>>n;
        string s;
        cin>>s;
        int res=s.size();
        if(n%2==0)
        {
            vector<int>v[2]={vector<int>(26),vector<int>(26)};
            for(int i=0;i<n;i++)
            {
                v[i%2][s[i]-'a']++;
            }
            for(int i=0;i<2;i++)
            {
                int mx=0;
                for(int j=0;j<26;j++)
                {
                    mx=max(mx,v[i][j]);
                }
                res-=mx;
            }
            cout<<res<<endl;
        }
        else
        {
            vector<int>pref[2]={vector<int>(26),vector<int>(26)};
            vector<int>suf[2]={vector<int>(26),vector<int>(26)};
            for(int i=n-1;i>=0;i--)
            {
                suf[i%2][s[i]-'a']++;
            }
            for(int i=0;i<n;i++)
            {
                suf[i%2][s[i]-'a']--;
                int ans=n;
                for(int k=0;k<2;k++)
                {
                    int mx=0;
                    for(int j=0;j<26;j++)
                    {
                        mx=max(mx,suf[1-k][j]+pref[k][j]);
                    }
                    ans-=mx;
                }
                res=min(res,ans);
                pref[i%2][s[i]-'a']++;
            }
            cout<<res<<endl;
        }
    }
}

t = int(input())
for _ in range(t):
    n = int(input())
    s = input()
    res = len(s)
    if n % 2 == 0:
        v = [[0] * 26 for _ in range(2)]
        for i in range(n):
            v[i % 2][ord(s[i]) - ord('a')] += 1
        for i in range(2):
            mx = max(v[i])
            res -= mx
        print(res)
    else:
        pref = [[0] * 26 for _ in range(2)]
        suf = [[0] * 26 for _ in range(2)]
        for i in range(n - 1, -1, -1):
            suf[i % 2][ord(s[i]) - ord('a')] += 1
        for i in range(n):
            suf[i % 2][ord(s[i]) - ord('a')] -= 1
            ans = n
            for k in range(2):
                mx = 0
                for j in range(26):
                    mx = max(mx, suf[1 - k][j] + pref[k][j])
                ans -= mx
            res = min(res, ans)
            pref[i % 2][ord(s[i]) - ord('a')] += 1
        print(res)

2008F - Sakurako's Box

#include <bits/stdc++.h>

using namespace std;
constexpr int mod=1e9+7;

long long binpow(long long a,long long b)
{
    if(b==0)
    {
        return 1;
    }
    if(b%2)
    {
        return (a*binpow(a,b-1))%mod;
    }
    return binpow((a*a)%mod,b/2);
}

int main(){
    int t;
    cin>>t;
    while(t--)
    {
        long long n;
        cin>>n;
        long long a[n],sum=0,sumsq=0;
        for(int i=0;i<n;i++)
        {
            cin>>a[i];
            sum+=a[i];sum%=mod;
            sumsq+=a[i]*a[i];
            sumsq%=mod;
        }
        sum*=sum;sum%=mod;
        sum=(sum-sumsq+mod)%mod;
        sum=(sum*binpow(2,mod-2))%mod;
        long long cnt=n*(n-1)/2;cnt%=mod;
        cout<<(sum%mod)*binpow(cnt,mod-2)%mod<<endl;
    }
}

import sys; input = sys.stdin.readline
for i in range(int(input())):
    n = int(input())
    a = list(map(int, input().split()))
    ans = 0
    s = 0
    mod = int(1e9 + 7)
    for i in range(n): s += a[i]
    s %= mod
    for i in range(n):
        s -= a[i]
        ans = (ans + a[i] * s) % mod
    ans = (ans * pow(n * (n - 1) // 2, mod - 2, mod)) % mod
    print(ans)
 

2008G - Sakurako's Task

#include <bits/stdc++.h>

using namespace std;

int main(){
    int t;
    cin>>t;
    while(t--)
    {
        int n,k;
        cin>>n>>k;
        long long a[n+1],g=0,mx=0;
        for(int i=0;i<n;i++)
        {
            cin>>a[i];
            g=__gcd(g,a[i]);
            mx=max(mx,a[i]);
        }
        if(g==0)
        {
            cout<<k<<endl;
            continue;
        }
        sort(a,a+n);
        int q=-g;
        if(n!=1)
        {
            for(int i=0;i<n;i++)
            {
                q+=g;
                a[i]=q;
            }
        }
        a[n]=1e16;
        long long lst=-1;
        for(int i=0;i<=n;i++)
        {
            if(k<=a[i]-lst-1)
            {
                break;
            }
            k-=max(a[i]-lst-1,0ll);
            lst=a[i];
        }
        cout<<lst+k<<endl;
    }
}

import math

t = int(input())
for _ in range(t):
    n, k = map(int, input().split())
    a = list(map(int, input().split()))
    g = 0
    mx = 0
    for i in range(n):
        g = math.gcd(g, a[i])
        mx = max(mx, a[i])
    if g == 0:
        print(k)
        continue
    a.sort()
    q = -g
    if n != 1:
        for i in range(n):
            q += g
            a[i] = q
    a.append(10**16)
    lst = -1
    for i in range(n + 1):
        if k <= a[i] - lst - 1:
            break
        k -= max(a[i] - lst - 1, 0)
        lst = a[i]
    print(lst + k)

2008H - Sakurako's Test

#include <bits/stdc++.h>

using namespace std;

int main()
{
    int t=1;
    cin>>t;
    for(int i=1;i<=t;i++)
    {
        int n,m;
        cin>>n>>m;
        vector<int>a(n);
        vector<int>c(n+1,0ll);
        for(int i=0;i<n;i++)
        {
            cin>>a[i];
            c[a[i]]++;
        }
        for(int i=1;i<=n;i++)
        {
            c[i]+=c[i-1];
        }
        int res[n+1]={0};
        for(int x=1;x<=n;x++)
        {
            int l=0,r=x;
            while(l<r)
            {
                int mid=(l+r)/2;
                int cnt=c[mid];
                for(int k=1;k*x<=n;k++)
                {
                    cnt+=c[min(k*x+mid,n)]-c[k*x-1];
                }
                if(cnt-1>=n/2)
                {
                    r=mid;
                }
                else
                {
                    l=mid+1;
                }
            }
            res[x]=l;
        }
        while(m--)
        {
            int x;
            cin>>x;
            cout<<res[x]<<" ";
        }
        cout<<endl;
    }
}

for _ in range(int(input())):
    n, m = map(int, input().split())
    a = list(map(int, input().split()))
    c = [0] * (n + 1)
    
    for i in range(n):
        c[a[i]] += 1
    
    for i in range(1, n + 1):
        c[i] += c[i - 1]
    
    res = [0] * (n + 1)
    
    for x in range(1, n + 1):
        l, r = 0, x
        while l < r:
            mid = (l + r) // 2
            cnt = c[mid]
            for k in range(1, n // x + 1):
                cnt += c[min(k * x + mid, n)] - c[k * x - 1]
            if cnt - 1 >= n // 2:
                r = mid
            else:
                l = mid + 1
        res[x] = l
    
    for _ in range(m):
        x = int(input())
        print(res[x])

Hello Codeforces!

I am pleased to invite you all to participate in Codeforces Round 970 (Div. 3), which will start on 01.09.2024 17:35 (Московское время).

The format of the event will be like any Div. 3 rounds:

• 6-8 tasks;

• ICPC rules with a penalty of 10 minutes for an incorrect submission;

• 12-hour phase of open hacks after the end of the round (hacks do not give additional points)

• after the end of the open hacking phase, all solutions will be tested on the updated set of tests, and the ratings recalculated

• by default, only "trusted" participants are shown in the results table.

I encourage participants with a rating of 1600+ not to create new accounts but to participate unofficially.

Only trusted participants of the third division will be included in the official standings table. This is a forced measure for combating unsporting behavior. To qualify as a trusted participant of the third division, you must:

• take part in at least five rated rounds (and solve at least one problem in each of them),
• do not have a point of 1900 or higher in the rating.

Regardless of whether you are a trusted participant of the third division or not, if your rating is less than 1600 (or you are a newcomer/unrated), then the round will be rated for you.

Also, it will be the first round with unrated register. If you already registered as rated participant you can change registration type here.

I would like to thank

• MikeMirzayanov for creating Codeforces and Polygon and testing the round.

• Vladosiya for beautiful coordination and helping in preparation.

• FBI, SashaT9 and Skillful_Wanderer for not only testing but also discussion of the problems.

• gmusya, Axial-Tilted, chen_zexing, Mr.Pie, XYZ_Herry, gvancak, Layk, CLown1331 and aboodsalman04 for testing and useful feedback.

Good luck!

UPD:

Editorial has been published.

I haven't seen anyone to write about this technique, so I decided to make a blog about it. I know that it is mostly general intuition, but not everyone really understand it. Also, I would be happy if you add something in comments or correct some errors. Also, before reading this blog I recommend to have some knowledge about segment tree and divide and conquer.

I would like to thank riazhskkh and FBI for reviewing this blog.

The main idea

When we have some divide and conquer algorithm, we can memorize each recursive call to be able to operate with it as data structure. For example, when we do merge sort, we can memorize how array looked after sorting on each call. Using this we can get merge sort tree. Also, if we memorize quick sort in such way, we will get wavelet tree. A lot of standart ways to use divide and conquer would lead to segment tree. But, it also can be used when we divide array on 3 parts or more, when we divide considering parity of indexes of array and so on. One of the main usage of it, that we can do almost all operation which we can do on segment tree, such as lazy propagation or tree descent, (in fact it depends on the task that we are solving) and in the most cases it optimize solutions alot. For example, if we havee recursion that recursevily divide array on even and odd elements,

void rec(vector<int>&v)
{
    int mx=0;
    vector<int>odd;
    vector<int>even;
    for(int i=0;i<v.size();i++)
    {
        mx=max(mx,v[i]);
        if(i%2==0)
        {
            even.push_back(v[i]/2);
        }
        else
        {
            odd.push_back(v[i]/2);
        }
    }
    if(mx==0)
    {
        return;
    }
    rec(even);
    rec(odd);
}

and assume we memorize at each level (even and odd array each time), then we can do lazy propagation here. For example, we can add $$$x$$$ to all elements on the segment $$$[l,r]$$$, in the same way as in the segment tree. But this recursion can also solve queries to add $$$x$$$ to all elements with even (or odd) indexes on the segment $$$[l,r]$$$, or such indexes that are equal 3 by modulo 4, or in general any index that has last $$$k$$$ bits equal to some number. Also, as you may see, if we replace indexes by numbers, we would get a classic binary tree (a prefix tree).

The problem

We will solve this problem.

Solution

Firstly, we will solve the problem without queries. To make it easier, we can change vertex numbers on the tree using DFS.

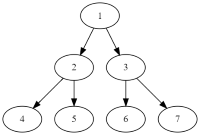For example, from this  as in the statement to this .

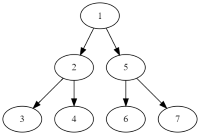After changing graph indexing, we can use divide and conquer to check if the permutation is good. In fact, for any vertex, all vertexes in its subtree after sorting should be continuous. It is true because of the way we change vertex numbers. So, it can be easily verified by just taking maximum and minimum of all subtrees and checking if there is the same number of elements between maximum and minimum as there is in the tree (It works because all elements are distinct). Important thing is that we can do it on segments, since segment [1,n] represents the whole tree, while segment [2, $$$\lfloor\frac{n+1}{2}\rfloor$$$ ] represents its right subtree, and segment [ $$$\lfloor\frac{n+1}{2}+1\rfloor$$$ ,n] represents its left subtree. Also, it is important to check if the depth of the vertex is the same. You see, in any DFS order, the depth of all vertices doesn't change, but it is easy to come up with a test, where divide and conquer solution will give yes and depths will be wrong.

// Check if a permutation correct on segment [l,r)
// d is array of depths. In other words, d[x] is the depth of a vertex x
bool check(int l,int r,int depth=0)
{
    if(l+1==r)
    {
        return 1;
    }
    int mid=(l+r)/2;
    return (depth==d[p[l]]&check(l+1,m)&check(m,r));
}

This solution works in $$$O(n\cdot log(n))$$$, but we can memorize all layers of a recursion call just like in the segment tree. In fact, all we need to memorize is a maximum and a minimum on a segment and if the segment is good (if check function from divide in conquer returns true or false). Then, we have queries which are to swap two elements. It is the same as changing the value of one element to the value of a second and vice versa for the second element, so all we need to be able to do is to change value of some element. Here, we can just memorize all states of recursion and make something like a segment tree, where segment [l,r) has children [l+1, $$$\lfloor\frac{l+r}{2}\rfloor$$$ ) and [ $$$\lfloor\frac{l+r}{2}\rfloor$$$ , r). So, it will work in $$$O(n\cdot log(n))$$$

Note

This technique can be used not only as binary tree like segment tree, trie or other, but also as another data structures. So, if you have tree with depth $$$g$$$, then you can answer the query in $$$O(g\cdot C)$$$ time where $$$C$$$ is number of operation needed to make decision to the child of the vertex. It means, that in path graph and star graph this will work in linear time per query.

So, you can solve the last problem not only when it is binary, but also when it is random generated. It is because the depth of the random generated tree is $$$O(log(n))$$$.

Also, I believe there could be a lot more tricks like this. Like taking random vertex as a root or doing same on any graph but on MST and so on. Unfortunetly, I have no samples for this yet.

We are excited to announce a new Weekend Practice round on August 3, at 19 UTC. This is a ranking competition at Eolymp.

Format and Difficulty

Same as in previous rounds, the competition is primarily aimed at improving practical skills. There will be 2.5 hours for 5 tasks of varying difficulty, the easiest of which can even be solved by beginners.

The scoring for each task being block-based (meaning points are awarded for each block of tests separately, and only if the solution passes all tests in the block). If there is a tie between two participants, the one whose last productive submission (i.e., a submission that added at least one point) was made earlier will be ranked higher in the leaderboard.

The statements will be available in the following languages: English, Ukrainian, French, Spanish, Azerbaijani, Russian.

Registration

You can join the competition on the competition page.

Prizes

The top-10 participants of the competition, as well as 10 random participants from those who rank from 11th to 100th place, will receive prizes in the form of t-shirts. Please, note, that we have changed how prizes are awarded,

Visit Frequently Asked Questions section to learn more.

Thanks a lot to:

• arsijo for coordinating the contest
• Sergey Kolodyazhnyy for creating Eolymp
• FBI, SashaT9, Pa_sha for authoring the problems
• Yam, MAKMED1337, Ignut, Vladosiya, Skillful_Wanderer, sashko123, waipoli for testing the contest

Sponsors

This round is sponsored by Pinely.

Pinely is a dynamic company, which deals with algorithmic trading is privately held and self-funded, with offices in Singapore, the Netherlands and Cyprus. We specialize in high-frequency and ultra-low latency trading, striving to be among the best trading companies in the world.

To join our team, please send your resume to [email protected].

UPD

Congrats to the winners:

• yutabi

• Anonymous_Noob

• davi_bart

• Agreb

• Denisov

• shevlopmes

• Chifwin

• Kaleem_Raza_Syed

• vladilius

• TheFuturoma

The editorial is available by the following links:

1. Sakurako's Birthday

2. Math Test

3. Party gathering

4. Long-Awaited Party

5. Sakurako and Old Dictionary

Hello Codeforces!

We are pleased to invite you all to participate in Codeforces Round 891 (Div. 3), which will start on 07.08.2023 17:35 (Московское время).

The format of the event will be like any Div. 3 rounds:

• 6-8 tasks;

• ICPC rules with a penalty of 10 minutes for an incorrect submission;

• 12-hour phase of open hacks after the end of the round (hacks do not give additional points)

• after the end of the open hacking phase, all solutions will be tested on the updated set of tests, and the ratings recalculated

• by default, only "trusted" participants are shown in the results table.

We encourage participants with a rating of 1600+ not to create new accounts but to participate unofficially.

Only trusted participants of the third division will be included in the official standings table. This is a forced measure for combating unsporting behavior. To qualify as a trusted participant of the third division, you must:

• take part in at least five rated rounds (and solve at least one problem in each of them),
• do not have a point of 1900 or higher in the rating.

Regardless of whether you are a trusted participant of the third division or not, if your rating is less than 1600 (or you are a newcomer/unrated), then the round will be rated for you.

Problems have been created and written by our team: FBI, Skillful_Wanderer, SashaT9 and Pa_sha.

We would like to thank

• MikeMirzayanov for creating Codeforces and Polygon.

• Vladosiya for coordination.

• nigus, YocyCraft, lis05, Nazar, welleyth, pavlekn, senjougaharin, Vladithur, DJeniUp, volochai, eggag32, moonpie24, shell_wataru, Kalashnikov, Bogdan1110, ksu_, zamong_juice, myav, sonyalytv for testing the round and making it better.

Good luck!

UPD: There was an error on problem F. We fixed the tests and rejudged solutions . We apologize for that. It only affected a few people whose solutions passes all tests now. Also some hacks were already added to the tests and broke some of solutions.

UPD2: Editorial