Предварительная версия разбора.
В задаче про четные и нечетные числа требуется понять, как будет выглядеть последовательность чисел от 1 до n, если выписать сначала все нечетные числа, а затем — четные. Для того, чтобы определить, какое число стоит на k-м месте, нужно посчитать индекс в массиве, с которого начнутся четные числа, и вывести соответствующее k либо нечетное число из первой половины массива, либо четное из второй.
В задаче про хэви-метал требуется найти в строке S количество подстрок, начинающихся на одну строчку A и заканчивающихся другой строчкой B. Если мы пометим черным все позиции вхождения в S строки A, белым — позиции вхождения строки B, то получим следующую задачу: посчитать количество пар <черная позиция, белая позиция> (причем именно в таком порядке). Для этого достаточно бежать, к примеру, слева направо и хранить счетчик — количество уже пройденных черных позиций. Тогда если мы встречаем очередную черную позицию, то увеличиваем счетчик на один, если встречаем белую — добавляем к ответу количество пар с данной белой позицией. А это количество — и есть текущее значение счетчика.
Как легко понять эта задача была задачей на аккуратность. В ней труднее не придумать решение, а написать его так, чтобы ни один случай не был забыт.
Каждый ход мы заменяем одно из чисел x, y на их сумму x + y и так пока пара чисел на доске не станет m-превосходной (то есть одно из чисел станет не меньше m). Ясно, что заменять на сумму нужно именно меньшее из двух чисел x и y. Действительно, будем говорить что пара чисел x1 ≤ y1 мажорирует пару чисел x2 ≤ y2, если y1 ≥ y2 и x1 ≥ y2. В этой ситуации, если за несколько наших действий из пары x2, y2 мы получим m-превосходную, то применяя те же самые действия к x1, y1 мы получим m-превосходную пару никак не позже. Если x ≤ y, то пара x + y, y мажорирует пару x + y, x. Поэтому путь через x + y, y до m-превосходной никак не длинее, и можно считать что мы выбираем именно эту пару. Теперь действия нашего игрока однозначны.
Рассмотрим случаи:
x ≤ 0, y ≤ 0 В этом случае наши операции не увеличивают числа на доске, поэтому пара может стать m-превосходной только если она изначально была m-превосходной.
x > 0 или y > 0 В этом случае для любого m пара со временем станет m-превосходной. Для того чтобы посчитать точное количество шагов теперь достаточно запустить эмуляцию. Однако если при x > 0 и y > 0 легко видеть что пара <<растет экспоненциально>> (формальнее: лекго видеть что начиная со второго шага сумма x + y увеличивается хотя бы в 3 / 2 раза за каждый ход) и эмуляция работает очень быстро, то в случае x < 0 и y > 0 (или наоборот) числа в паре могут изменяться очень медленно. Особенно хорошо это видно на примере x = - 1018, y = 1. Поэтому в таком случае необходимо отдельно посчитать количество шагов до момента, когда оба числа станут неотрицательными и только потом запускать эмуляцию. Для x < 0 и y > 0 такое количество шагов равно
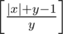 .
.
Задачу можно представлять себе следующим образом. В вершинах двумерной решетки 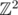 расставлены неотрицательные целые числа A(x, y). Считаем, что они заданы функцией
расставлены неотрицательные целые числа A(x, y). Считаем, что они заданы функцией 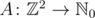 . В каждый момент времени для каждой вершины P = (x, y) с числом A(x, y) ≥ 4 применяется операция φP, которая уменьшает A(x, y) на 4 и увеличивает A(x, y - 1), A(x, y + 1), A(x - 1, y), A(x + 1, y) на 1. Можно считать, что операция φP применяется ко всей функции A. От нас требуется найти эту функцию в запрашиваемых узлах после того как итерации прекратятся.
. В каждый момент времени для каждой вершины P = (x, y) с числом A(x, y) ≥ 4 применяется операция φP, которая уменьшает A(x, y) на 4 и увеличивает A(x, y - 1), A(x, y + 1), A(x - 1, y), A(x + 1, y) на 1. Можно считать, что операция φP применяется ко всей функции A. От нас требуется найти эту функцию в запрашиваемых узлах после того как итерации прекратятся.
Ключевое наблюдение для большинства решений состояло в том, что операции φP и φQ для всех точек P и Q коммутируют, то есть φP(φQ(A)) = φQ(φP(A)). Поэтому неважно в каком именно порядке применять операции. В частности, можно считать, что из данной вершины разбегаются сразу все возможные четверки муравьев. Теперь можно запустить прямую эмуляцию процесса в таком виде. В качестве упражнения участникам предлагается проверить, что муравьи никогда не покинут квадрат 200 × 200 с центром в 0 при указанных ограничениях.
В задаче про сосуды и воду требовалось найти последовательность из порядка n2 переливаний, которая переводит начальную конфигурацию в конечную. Во-первых, утверждается следующее: если в каждой компоненте связности сумма исходных значений и сумма итоговых совпадают, то ответ существует. Назовем сосуд готовым, если текущее и требуемое количество воды в нем совпадают. Опишем сначала решение, которое, вероятно, проще всего пишется. Будем делать сосуды готовыми по очереди. Возьмем произвольную пару еще не готовых сосудов s и t (в s сейчас воды больше, чем нужно, в t — меньше, чем нужно), такую, что их соединяет некоторый простой путь P, при этом если перелить из s в t d литров, то один из сосудов станет готовым. Осталось научиться переливать d литров по пути из s в t. Напишем для этого рекурсивную функцию pour(s, t, d). Пусть t' идет перед t в этом пути, тогда функцию выполнит следующее: перельет из t' сколько возможно (разумеется, не больше d) в t, вызовет pour(s, t', d) и затем перельет из t' в t то, что осталось. Несложно проверить, что никакой сосуд при этом не переполнится. Такой алгоритм производит переливание по пути длины len за 2len элементарных переливаний, в итоге решение делает не более 2n2 операций.
Давайте для каждого числа x обозначим последовательность его степеней не вылезающих за границы [1..n] через Pow(x): 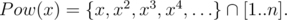
Тогда наша игра состоит в следующем: каждый игрок на очередном шаге выбирает еще не зачеркнутое число x от 1 до n и зачеркивает все числа из Pow(x). Проигрывает не имеющий хода.
Легко заметить, что такая игра распадается в сумму нескольких более простых игр. Действительно, назовем число x примитивным (и соответствующую последовательность Pow(x) примитивной), если оно не является степенью никакого числа y < x. Тогда: 1. для любого числа 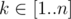 найдется примитивное число x, такое что
найдется примитивное число x, такое что 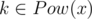 ; 2. для любых различных примитивных чисел x и y множества Pow(x) и P(y) не пересекаются. Действительно для данного числа k существует ровно одно примитивное x степенью которого k является. Это, например, следует из основной теоремы арифметики: если
; 2. для любых различных примитивных чисел x и y множества Pow(x) и P(y) не пересекаются. Действительно для данного числа k существует ровно одно примитивное x степенью которого k является. Это, например, следует из основной теоремы арифметики: если 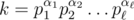 и d = gcd(α1, α2, ..., αn), то
и d = gcd(α1, α2, ..., αn), то 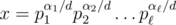 .
.
Таким образом все множество [1..n] разбивается на маленькие примитивные подмножества Pow(x), игра на которых происходит независимо. Наша игра распалась в сумму меньших игр. Теперь необходимо применить теорию Шпрага-Гранди и заметить, что мекс-функция нашей игры является ксором мекс-функций всех игр на примитивных Pow(x). Среди таких игр много совпадающих, что позволит легко вычислить ксор.
Для конкретного x, если Pow(x) = {x, x2, ..., xs}, то мекс-функция зависит только от s, но не от самого x. В наших ограничениях s принимает значения от 1 до 29, мекс-функции для всех таких s можно предподсчитать напрямую. Осталось теперь лишь найти количество q(s) примитивных x с данной длиной Pow(x) равной s (более точно нас интересует не количество, а лишь четность этого количества).
Ограничения задачи позволяют сделать это "в лоб": увеличиваем x от 2 до  , если оно не зачеркнуто, находим длину Pow(x) [увеличиваем соответствующее q(s)], и зачеркиваем все числа из Pow(x).
, если оно не зачеркнуто, находим длину Pow(x) [увеличиваем соответствующее q(s)], и зачеркиваем все числа из Pow(x).
Этот цикл найдет все примитивные последовательности длины хотя бы 2. Количество незачеркнутых чисел даст все примитивные последовательности длины 1. Останется лишь посмотреть на их четности и посчитать соответсвующий ксор мексов.
Однако можно найти все q(s) и за 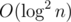 . Действительно, давайте посмотрим какое-нибудь число
. Действительно, давайте посмотрим какое-нибудь число 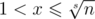 и последовательность {x, x2, x3, x4, ..., xs}. Она не является примитивной, только если содержится как подмножество в некоторой большей примитивной последовательности. Количество таких подпоследовательностей длины s в данной примитивной последовательности длины t > s легко найти, действительно это [t / s]. Вспоминая теперь, что притимвные последовательности не пересекаются получаем реккуретную формулу
и последовательность {x, x2, x3, x4, ..., xs}. Она не является примитивной, только если содержится как подмножество в некоторой большей примитивной последовательности. Количество таких подпоследовательностей длины s в данной примитивной последовательности длины t > s легко найти, действительно это [t / s]. Вспоминая теперь, что притимвные последовательности не пересекаются получаем реккуретную формулу
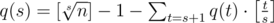 .
.
Используя ее, легко найти все q(s) начиная с q(29) и заканчивая q(1).
Замечание: при написании задачи важно не забыть учесть примитивное x = 1.
В задаче про принцессу Владу требовалось всего-навсего поймать тень. Опишем идею решения. Если на плоскости растет всего одно дерево, то, используя его как преграду для тени, несложно найти подходящую последовательность ходов. Аналогично поступим (использовав какое-либо крайнее дерево), если Влада и Тень находятся далеко, вне квадрата, где могут расти деревья. Осталось понять, что же делать в самой чаще леса! Если между Владой и ее тенью вообще не существует пути, то поймать тень никак не удастся. Иначе рассмотрим кратчайший путь от принцессы до тени, и пойдем принцессой по нему. Будет считать, что этот путь задает нам очередь шагов, которые необходимо сделать. При этом если тень передвигается куда-либо, то добавим ее ход в очередь (иначе говоря, мы идем по пути, состоящему из кратчайшего пути до тени в начальный момент времени и последующих передвижений тени). Алгоритмическая часть на этом закончилась: утверждается, что мы за необходимое число шагов либо поймаем тень, либо выйдем из "лесного квадрата". Доказательство опирается на следующую идею: длина пути, по которому мы идем до тени, разве что уменьшается. При этом если она не уменьшается достаточно долго, то раз в k шагов (k — длина пути) происходит смещение на один и тот же ненулевой вектор, следовательно, мы выйдем из "лесного квадрата". Стоит отметить, что если наши герои не заперты в лабиринт (могут выйти из "лесного квадрата"), то можно вывести их из квадрата по очереди. Но в таком случае для лабиринта все равно придется придумывать способ ловить тень.










