Could not find any post for today's open cup. Let's discuss the problems here. How to solve F and G?
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
6 дней
Зарегистрироваться »
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Can someone please give any idea about how to solve problem G.Tourist of this set?
The problem basically gives you a directed graph, a source, a destination and a list of interesting nodes. You have to start from the source and reach the destination and visit all the interesting nodes on your path. You are allowed to visit a node multiple times but you cannot use more than n^2 nodes in your path. You have to print the path or say it is not possible. Number of nodes is 2000 and number of edges can be 2000*2000.
I have a O(V*E) solution for the problem. But that is not going to be enough. Can someone give any better idea?
I have been stuck at this problem for a while.
In this problem, there is a rectangular grid where some of the cells are blocked and others are empty. Player 1 can pick any cell to start the game. After that, the second player will be able to pick any adjacent cell of the last picked cell in his move, which has not been picked before. And then the game will continue in this way. The player who cannot pick any cell in his move will lose. We need to know if the first player can win if both play optimally.
These are the links that I've found to follow World Finals live.
Live Analysis by Tourist, Petr and Endagorian . Details about it here
Problems of the contest: ( Probably we would be able to submit solutions some time after the contest has started )
Is there anything more that should be followed ?
I've been trying to understand Dinic's Max Flow algorithm. I think I've fairly understood how the algorithm works.
In each iteration, you create a level graph using BFS and then find blocking flow in that level graph. You would need O(N) iterations and in each iteration, blocking flow can be found in O(NM) complexity. This is the place where I'm stuck. I've seen some implementations like Stanford Notebook Dinic implementation . But it seems to me that in the worst case you might need O(M^2) complexity to find the blocking flow if you implement the code this way. Can anyone help me to understand why the complexity is O(NM) for finding blocking flow ?
Hello Codeforces!
On Thursday, 20 April 2017, 13:00:00 GMT , an online mirror of the Bangladesh National High School Programming Contest (NHSPC 2017) will be held at Codeforces Gym.
The problems were prepared by :
Riddho, immuntasir, Jami_CSEDU, nafisiham, prophet_ov_darkness, raida_ash, shadowfax, Tanzir5 and bertho_coder.
This is an individual contest hosted as a preliminary selection contest for IOI participants of Bangladesh. You will have 3 hours to solve the problems. The setters have decided to rate the difficulty of the contest to be 3 stars. There's a wide variety of problems and we hope that you would enjoy the problems in general and have fun solving the contest.
Best of luck.
Update1:
The contest has finished. The top 5 are:
Thanks everyone. The editorial will be posted very soon.
Update2:
Editorial has been published.
This is a problem that appeared in Hong Kong regional 2016. Only one team could solve it. In this problem, you have to find a valid closed tour in a n*m board ( 1< = n,m <= 200) where two consecutive cells in your path must have a Manhattan distance of 2 or 3 and every cell is visited exactly once. Or you should output that no valid tour is possible.
This seemed to me like a variation of a knight's tour problem on an arbitrary sized chessboard where you're allowed to move like a chess knight. I've read up a bit on Warnsdorf's rule . I was not sure if it would help here. Nonetheless I implemented the rule in this code to check its efficiency for this problem. As expected, it doesn't even work for boards like 7*7.
So does anyone have any idea how this problem can be solved ?
There are 3 contests scheduled in 3 days! That's new! Just asking, has this happened before ? :P 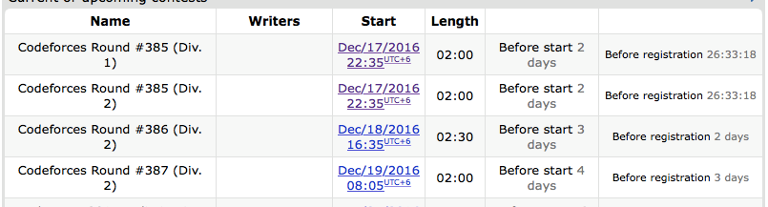
I was wondering if there is any way to solve the following problem:
" You are given a network graph. Every edge has two values associated with it: the upper bound of the amount of flow that CAN go through this edge and the lower bound of the amount of flow that MUST go through this edge. If there is no valid way to satisfy lower bound of all the edges, print "Unsolvable" . If there are multiple ways, maximize the amount of flow satisfying the lower bounds and upper bounds. You have to report the maximum amount and also the amount of flows through individual edges. "
I don't know of any online judge that has this problem. It's a random problem that came to my mind.
I was trying to solve this problem and found this in wiki. I am referring to the fourth application here, "Image Segmentation Problem". I think I need to understand this to solve the above problem. But the wiki article only says what to do to solve image segmentation problem. But it doesn't explain the logic or idea behind it. Can anyone help me to understand it ?
This is what is written in Wikipedia:

How can I solve the problem "The Stones Game" from Africa/Middle East — Arab Regionals 2013 ? Any help or hint would be appreciated. https://icpcarchive.ecs.baylor.edu/index.php?option=com_onlinejudge&Itemid=8&category=592&page=show_problem&problem=4772
| Название |
|---|










