Hola Codeforces community! Sorry for the delay, we were solving some details of our national contest. We hope you enjoyed and learned a lot from this contest, we made it with much love. Our team worked day and night these last days to make sure you had a valuable experience :)). If you have any doubts about the editorial, please let us know in the comments, we are happy to help you. The editorial was prepared by jampm and me. Btw, best meme of the round.
2022A - Bus to Pénjamo
The key to maximizing happiness is to seat family members together as much as possible. If two members of the same family sit in the same row, both will be happy, and we only use two seats. However, if they are seated separately, only one person is happy, but two seats are still used. Therefore, we prioritize seating family pairs together first.
Once all possible pairs are seated, there may still be some family members left to seat. If a family has an odd number of members, one person will be left without a pair. Ideally, we want to seat this person alone in a row to make them happy. However, if there are no remaining rows to seat them alone, we’ll have to seat them with someone from another family. This means the other person might no longer be happy since they are no longer seated alone.
The easiest way to handle part 2 is to check the number of remaining rows and people. If the number of remaining rows is greater than or equal to the number of unpaired people, all unpaired people can sit alone and remain happy. Otherwise, some people will have to share a row, and their happiness will be affected. In that case, the number of happy people will be $$$2 \times$$$ remaining rows $$$-$$$ remaining people.
#include <bits/stdc++.h>
using namespace std;
int main() {
int t;
cin>>t;
while(t--)
{
int n,r;
cin>>n>>r;
vector<int>arr(n);
int leftalone=0;
int happy=0;
for(int k=0;k<n;k++)
{
cin>>arr[k];
happy+=(arr[k]/2)*2;
r-=arr[k]/2;
leftalone+=arr[k]%2;
}
if(leftalone>r)
happy+=r*2-leftalone;
else
happy+=leftalone;
cout<<happy<<endl;
}
}
- Write down key observations and mix them to solve the problem
2022B - Kar Salesman
Since no customer can buy more than one car from the same model, the minimum number of clients we need is determined by the model with the most cars. Therefore, we need at least:
clients, because even if a customer buys cars from other models, they cannot exceed this limit for any single model.
Each client can buy up to $$$x$$$ cars from different models. To distribute all the cars among the clients, we also need to consider the total number of cars. Thus, the minimum number of clients needed is at least:
This ensures that all cars can be distributed across the clients, respecting the limit of $$$x$$$ cars per customer.
The actual number of clients required is the maximum of the two values:
This gives us a lower bound for the number of clients required, satisfying both constraints (the maximum cars of a single model and the total number of cars).
Apply binary search on the answer.
To demonstrate that this is always sufficient, we can reason that the most efficient strategy is to reduce the car count for the models with the largest numbers first. By doing so, we maximize the benefit of allowing each client to buy up to $$$x$$$ cars from different models.
After distributing the cars, two possible outcomes will arise:
All models will have the same number of remaining cars, and this situation will be optimal when the total cars are evenly distributed (matching the $$$\displaystyle\left\lceil \frac{a_1 + a_2 + ... + a_n}{x}\right\rceil$$$ bound).
There will be still a quantity of models less than or equal to x remaining, which matches the case where the maximum number of cars from a single model $$$\max(a_1, a_2, ..., a_n)$$$ determines the bound.
Imagine a grid of size $$$w \times x$$$, where $$$w$$$ represents the minimum number of clients needed:
Now, place the cars in this grid by filling it column by column, from the first model to the $$$n$$$-th model. This method ensures that each client will buy cars from different models and no client exceeds the $$$x$$$ car limit. Since the total number of cars is less than or equal to the size of the grid, this configuration guarantees that all cars will be sold within $$$w$$$ clients.
#include <bits/stdc++.h>
using namespace std;
int main() {
int t;
cin>>t;
while(t--)
{
long long n,x;
cin>>n>>x;
vector<long long>arr(n);
long long sum=0;
long long maximo=0;
for(int k=0;k<n;k++)
{
cin>>arr[k];
maximo=max(maximo,arr[k]);
sum+=arr[k];
}
long long sec=(sum+x-1)/(long long)x;
cout<<max(maximo,sec)<<endl;
}
}
- If you don't know how to solve a problem, try to solve for small cases to find a pattern.
2022C - Gerrymandering
We will use dynamic programming to keep track of the maximum number of votes Álvaro can secure as we move from column to column (note that there are many ways to implement the DP, we will use the easiest to understand).
An important observation is that if you use a horizontal piece in one row, you also have to use it in the other to avoid leaving holes.
Let $$$dp[i][j]$$$ represent the maximum number of votes Álvaro can get considering up to the $$$i$$$-th column. The second dimension $$$j$$$ represents the current configuration of filled cells:
- $$$j = 0$$$: All cells up to the $$$i$$$-th column are completely filled (including $$$i$$$-th).
- $$$j = 1$$$: All cells up to the i-th column are completely filled (including $$$i$$$-th), and there’s one extra cell filled in the first row of the next column. $$$j = 2$$$: The $$$i$$$-th column is filled, and there’s one extra cell filled in the second row of the next column.
For simplicity, we will call "L", "second L", "third L", and "fourth L" respectively the next pieces:
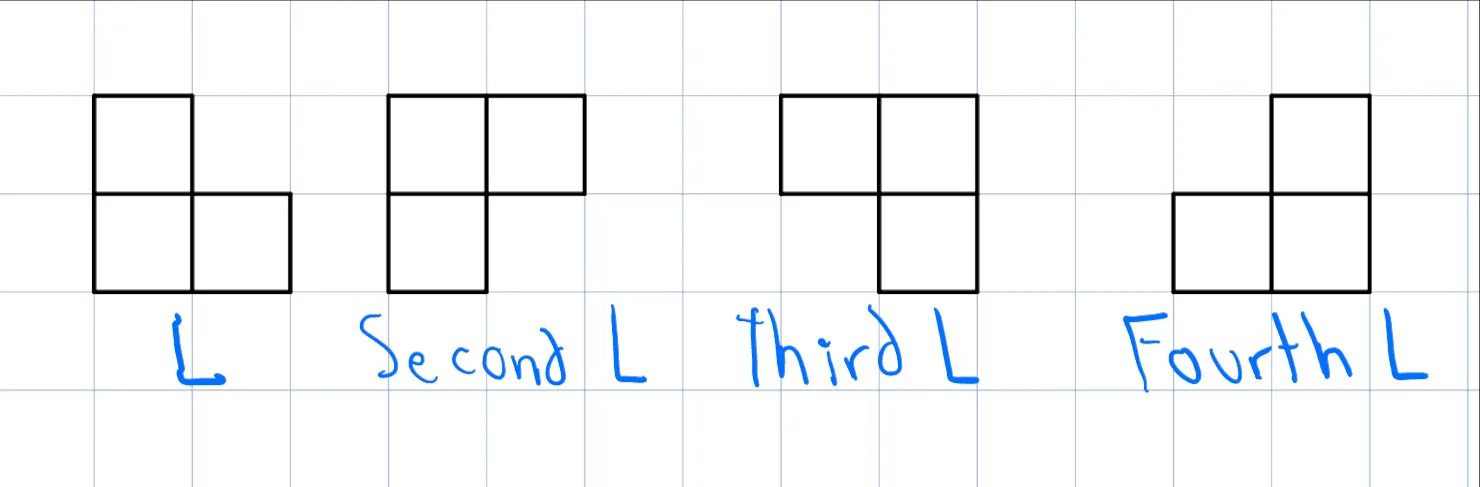
- From $$$dp[k][0]$$$ (Both rows filled at column $$$k$$$):
- You can place a horizontal piece in both rows, leading to $$$dp[k+3][0]$$$.
- You can place a first L piece, leading to $$$dp[k+1][1]$$$.
- You can place an L piece, leading to $$$dp[k+1][2]$$$.
- From $$$dp[k][1]$$$ (One extra cell in the first row of the next column):
- You can place a horizontal piece in the first row occupying from $$$k+2$$$ to $$$k+4$$$ and also a horizontal piece in the second row from $$$k+1$$$ to $$$k+3$$$, leading to $$$dp[k+3][1]$$$.
- You can place a fourth L, leading to $$$dp[k+2][0]$$$.
- From $$$dp[k][2]$$$ (One extra cell in the second row of the next column):
- You can place a horizontal piece in the first row occupying from $$$k+1$$$ to $$$k+3$$$ and also a horizontal piece in the second row from $$$k+2$$$ to $$$k+4$$$, leading to $$$dp[k+3][2]$$$.
- You can place a third L, leading to $$$dp[k+2][0]$$$.
More formally for each DP state, the following transitions are possible:
From $$$dp[k][0]$$$:
From $$$dp[k][1]$$$:
From $$$dp[k][2]$$$:
To implement the DP solution, you only need to handle the transitions for states $$$dp[i][0]$$$ and $$$dp[i][1]$$$. For $$$dp[i][2]$$$, the transitions are the same as $$$dp[i][1]$$$, with the rows swapped.
#include <bits/stdc++.h>
using namespace std;
void solve()
{
int n;
cin>>n;
vector<string>cad(n);
vector<vector<int> >vot(2,vector<int>(n+8));
for(int k=0;k<2;k++)
{
cin>>cad[k];
for(int i=0;i<n;i++)
if(cad[k][i]=='A')
vot[k][i+1]=1;
}
vector<vector<int> >dp(n+9,vector<int>(3,-1));
dp[0][0]=0;
for(int k=0;k<=n-1;k++)
{
for(int i=0;i<3;i++)
{
if(dp[k][i]!=-1)
{
int vt=0,val=dp[k][i];
if(i==0)
{
// *
// *
vt=(vot[0][k+1]+vot[0][k+2]+vot[0][k+3])/2+(vot[1][k+1]+vot[1][k+2]+vot[1][k+3])/2;
dp[k+3][0]=max(vt+val,dp[k+3][0]);
vt=(vot[1][k+1]+vot[0][k+2]+vot[0][k+1])/2;
dp[k+1][1]=max(vt+val,dp[k+1][1]);
vt=(vot[1][k+1]+vot[1][k+2]+vot[0][k+1])/2;
dp[k+1][2]=max(vt+val,dp[k+1][2]);
}
if(i==1)
{
// **
// *
vt=(vot[0][k+2]+vot[0][k+3]+vot[0][k+4])/2+(vot[1][k+1]+vot[1][k+2]+vot[1][k+3])/2;
dp[k+3][1]=max(vt+val,dp[k+3][1]);
vt=(vot[1][k+1]+vot[1][k+2]+vot[0][k+2])/2;
dp[k+2][0]=max(vt+val,dp[k+2][0]);
}
if(i==2)
{
//*
//**
vt=(vot[1][k+2]+vot[1][k+3]+vot[1][k+4])/2+(vot[0][k+1]+vot[0][k+2]+vot[0][k+3])/2;
dp[k+3][2]=max(vt+val,dp[k+3][2]);
vt=(vot[0][k+1]+vot[0][k+2]+vot[1][k+2])/2;
dp[k+2][0]=max(vt+val,dp[k+2][0]);
}
}
}
}
cout<<dp[n][0]<<endl;
}
int main() {
int t;
cin>>t;
while(t--)
solve();
}
- Don't begin to implement until all the details are very clear, this will make your implementation much easier.
- Draw images to visualize easier everything.
2022D1 - Asesino (Easy Version)
Try to do casework for small $$$n$$$. It is also a good idea to simulate it. Think about this problem as a directed graph, where for each query there is a directed edge.
Observe that if you ask $$$u \mapsto v$$$ and $$$v \mapsto u$$$, both answers will match if and only if $$$u$$$ and $$$v$$$ are not the impostor. This can be easily shown by case work.
We can observe that $$$n = 3$$$ and $$$n = 4$$$ are solvable with $$$4$$$ queries. This strategies are illustrated in the image below: 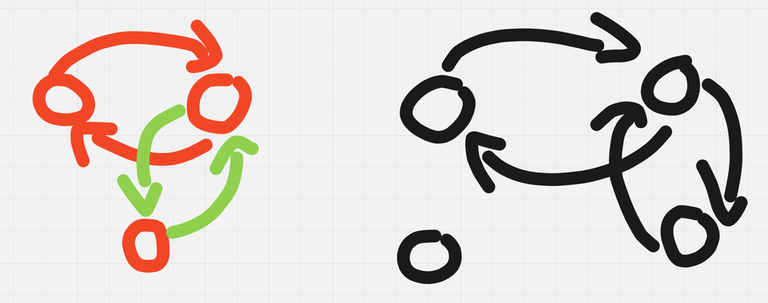
There's many solutions that work. Given that 69 is big enough, we can use the previous observation of asking in pairs and reducing the problem recursively.
Combining hint 2 with our solutions for $$$n = 3$$$ and $$$n = 4$$$, we can come up with the following algorithm:
While $$$n > 4$$$,
- query $$$n \mapsto n - 1$$$ and $$$n - 1 \mapsto n$$$.
- If their answers don't match, one of them is the impostor. Query $$$n \mapsto n - 2$$$ and $$$n - 2 \mapsto n$$$.
- If their answers don't match, $$$n$$$ is the impostor.
- Otherwise, $$$n - 1$$$ is the impostor.
- If the answers match, do $$$n -= 2$$$.
- If their answers don't match, one of them is the impostor. Query $$$n \mapsto n - 2$$$ and $$$n - 2 \mapsto n$$$.
- query $$$n \mapsto n - 1$$$ and $$$n - 1 \mapsto n$$$.
If $$$n > 4$$$ doesn't hold and we haven't found the impostor, we either have the $$$n = 3$$$ case or the $$$n = 4$$$ case, and we can solve either of them in $$$4$$$ queries.
In the worst case, this algorithm uses $$$n + 1$$$ queries. I'm also aware of a solution with $$$n + 4$$$ queries, $$$n + 2$$$ queries, and one with $$$n + \lceil\log(n)\rceil$$$ queries. We only present this solution to shorten the length of the blog but feel free to ask about the others in the comments.
#include <bits/stdc++.h>
using namespace std;
bool query(int i, int j, int ans = 0) {
cout << "? " << i << " " << j << endl;
cin >> ans;
return ans;
}
int main() {
int tt;
for (cin >> tt; tt; --tt) {
int n, N; cin >> N; n = N;
array<int, 2> candidates = {-1, -1};
while (n > 4) {
if (query(n - 1, n) != query(n, n - 1)) {
candidates = {n - 1, n}; break;
} else n -= 2;
}
if (candidates[0] != -1) {
int not_candidate = (candidates[0] == N - 1) ? N - 2 : N;
if (query(candidates[0], not_candidate) != query(not_candidate, candidates[0])) {
cout << "! " << candidates[0] << endl;
} else cout << "! " << candidates[1] << endl;
} else {
if (n == 3) {
if (query(1, 2) == query(2, 1)) cout << "! 3\n";
else {
if (query(1, 3) == query(3, 1)) cout << "! 2\n";
else cout << "! 1\n";
}
} else {
if (query(1 , 2) != query(2, 1)) {
if (query(1, 3) == query(3, 1)) cout << "! 2\n";
else cout << "! 1\n";
} else {
if (query(1, 3) != query(3, 1)) cout << "! 3\n";
else cout << "! 4\n";
}
}
}
}
}
2022D2 - Asesino (Hard Version)
What is the minimal value anyway? Our solution to D1 used $$$n$$$ queries if $$$n$$$ is even and $$$n + 1$$$ queries when $$$n$$$ is odd. Is this the optimal strategy? Can we find a lower bound? Can we find the optimal strategy for small $$$n$$$?
There's only $$$9$$$ possible unlabeled directed graphs with $$$3$$$ nodes and at most $$$3$$$ edges, you might as well draw them. They are illustrated in the image below for convenience though. Stare at them and convince yourself $$$4$$$ queries is the optimal for $$$n = 3$$$.

We would have to prove that $$$n - 1 < f(n)$$$ for all $$$n$$$ and $$$n < f(n)$$$ for $$$n$$$ odd. How could we structure a proof?
For $$$n - 1$$$ we have some control over the graph. We can show by pigeonhole principle that at least one of them has in-degree $$$0$$$, and at least one of them has out-degree $$$0$$$.
If those two nodes are different, call $$$A$$$ the node with in-degree $$$0$$$ and $$$B$$$ the node with out-degree $$$0$$$. Let the grader always reply yes to your queries.
- $$$A$$$ can be the impostor and everyone else Knaves.
- $$$B$$$ can be the impostor and everyone else Knights.
If those two nodes are the same, then the graph looks like a collection of cycles and one isolated node. The grader will always reply yes except for the last query where it replies no. Let the last query be to player $$$A$$$ about player $$$B$$$. The two assignments of roles are:
- $$$A$$$ is the impostor and everyone else in the cycle is a Knight.
- $$$B$$$ is the impostor and everyone else in the cycle is a Knave.
Note that the structure of our proof is very general and is very easy to simulate for small values of $$$n$$$ and small number of queries. Can we extend it to $$$n$$$ odd and $$$n$$$ queries? Try writing an exhaustive checker and run it for small values. According to our conjecture, $$$n = 5$$$ shouldn't solvable with $$$5$$$ queries. So we should find a set of answers that for any queries yields two valid assignments with different nodes as the impostor.
It doesn't exist! Which means $$$n = 5$$$ is solvable with $$$5$$$ queries. How? Also, observe that if we find a solution to $$$n = 5$$$ we can apply the same idea and recursively solve the problem in $$$n$$$ queries for all $$$n > 3$$$.
Consider the natural directed graph representation, adding a directed edge with weight $$$0$$$ between node $$$i$$$ and $$$j$$$ if the answer to the query ''? i j'' was yes, and a $$$1$$$ otherwise. We will also denote this query by $$$i \mapsto j$$$.
We will use a lemma, that generalizes the idea for D1.
Lemma:
The sum of weights of a cycle is odd if and only if the impostor is among us (among the cycle, I mean).
- Suppose the impostor is not in the cycle. Then observe that the only time you get an edge with weight $$$1$$$ is whenever there are two consecutive nodes with different roles. — Consider consecutive segments of nodes with the same role in this cycle, and compress each of this segments into one node. The image bellow illustrates how, grey edges are queries with answer no.
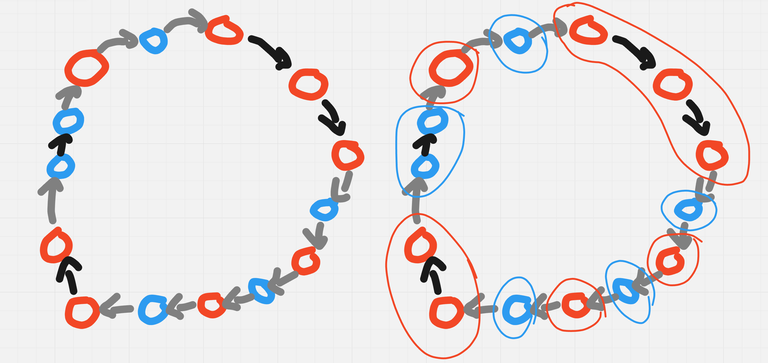
The new graph is bipartite, and thus has an even number of edges. But all the edges in this new graph, are all the grey edges in the original graph, which implies what we want.
If the impostor is in the cycle, there are three ways of inserting it (assume the cycle has more than $$$2$$$ nodes that case is exactly what we proved in hint 2).
- We can insert the impostor into one of this ``segments'' of consecutive nodes with the same role. This would increase the number of grey edges by $$$1$$$, changing the parity,
- We can insert it between two segments.
- If we have Knight $$$\mapsto$$$ Impostor $$$\mapsto$$$ Knave, the number of grey edges decreases by $$$1$$$.
- If thee is Knave $$$\mapsto$$$ Impostor $$$\mapsto$$$ Knight, the number of grey edges increases by $$$1$$$.
Either way, we changed the parity of the cycle. $$$\blacksquare$$$
The algorithm that solves the problem is the following:
If $$$n = 3$$$,
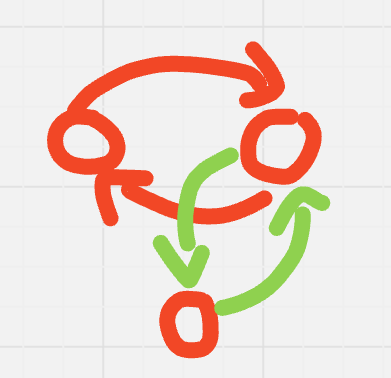
query $$$1 \mapsto 2$$$ and $$$2 \mapsto 1$$$,
If queries match, $$$3$$$ is the impostor.
Else, query $$$1 \mapsto 3$$$ and $$$3 \mapsto 1$$$.
- If queries match, $$$2$$$ is the impostor.
- Else, $$$1$$$ is the impostor.
Else, $$$n > 3$$$. To solve $$$n > 3$$$ players with $$$n$$$ queries, do:
While $$$n > 5$$$,
- query $$$n \mapsto n - 1$$$ and $$$n - 1 \mapsto n$$$.
- If their answers don't match, one of them is the impostor. Query $$$n \mapsto n - 2$$$ and $$$n - 2 \mapsto n$$$.
- If their answers don't match, $$$n$$$ is the impostor.
- Otherwise, $$$n - 1$$$ is the impostor.
- If the answers match, do $$$n -= 2$$$.
- If their answers don't match, one of them is the impostor. Query $$$n \mapsto n - 2$$$ and $$$n - 2 \mapsto n$$$.
- query $$$n \mapsto n - 1$$$ and $$$n - 1 \mapsto n$$$.
If $$$n > 5$$$ doesn't hold and we haven't found the impostor, we either have the $$$n = 4$$$ case or the $$$n = 5$$$ case, we solve them optimally in $$$4$$$ or $$$5$$$ queries each.
To solve $$$n = 5$$$ in $$$5$$$ queries,
We will form a cycle of size $$$3$$$, asking for $$$1 \mapsto 2$$$, $$$2 \mapsto 3$$$ and $$$3 \mapsto 2$$$ (blue edges in the image below).
- If the cycle has an even number of no's, we know the impostor is among $$$4$$$ or $$$5$$$. So we ask $$$3 \mapsto 4$$$ and $$$4 \mapsto 3$$$ (green edges).
- If both queries match, $$$5$$$ is the impostor.
- Else, $$$4$$$ is the impostor.
- Else, The impostor is among us (among the cycle, I mean). Ask $$$1 \mapsto 3$$$ and $$$2 \mapsto 1$$$ (purple edges).
- If $$$1 \mapsto 2$$$ doesn't match with $$$2 \mapsto 1$$$ and $$$1 \mapsto 3$$$ doesn't match with $$$3 \mapsto 1$$$, $$$1$$$ is the impostor.
- If $$$1 \mapsto 2$$$ doesn't match with $$$2 \mapsto 1$$$ and $$$1 \mapsto 3$$$ matches with $$$3 \mapsto 1$$$, $$$2$$$ is the impostor.
- If $$$1 \mapsto 2$$$ matches with $$$2 \mapsto 1$$$ and $$$1 \mapsto 3$$$ doesn't match with $$$3 \mapsto 1$$$, $$$3$$$ is the impostor.
- It is impossible for $$$1 \mapsto 2$$$ to match with $$$2 \mapsto 1$$$ and $$$1 \mapsto 3$$$ to match with $$$3 \mapsto 1$$$, because we know at least one of this cycles will contain the impostor.
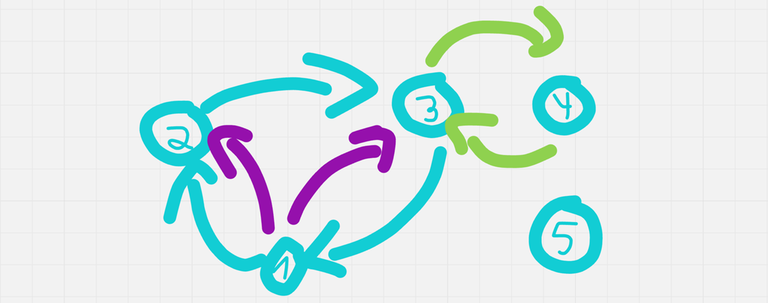
To solve $$$n = 4$$$ in $$$4$$$ queries,
We will query $$$1 \mapsto 2$$$, $$$2 \mapsto 1$$$, $$$1 \mapsto 3$$$ and $$$3 \mapsto 1$$$.
- If $$$1 \mapsto 2$$$ doesn't match with $$$2 \mapsto 1$$$ and $$$1 \mapsto 3$$$ doesn't match with $$$3 \mapsto 1$$$, $$$1$$$ is the impostor.
- If $$$1 \mapsto 2$$$ doesn't match with $$$2 \mapsto 1$$$ and $$$1 \mapsto 3$$$ matches with $$$3 \mapsto 1$$$, $$$2$$$ is the impostor.
- If $$$1 \mapsto 2$$$ matches with $$$2 \mapsto 1$$$ and $$$1 \mapsto 3$$$ doesn't match with $$$3 \mapsto 1$$$, $$$3$$$ is the impostor.
- If $$$1 \mapsto 2$$$ matches with $$$2 \mapsto 1$$$ and $$$1 \mapsto 3$$$ matches with $$$3 \mapsto 1$$$, then $$$4$$$ is the impostor.
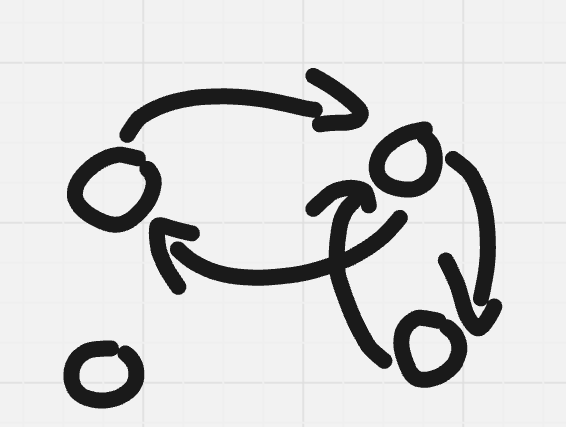
We have proven that that $$$f(n) \le \max(4, n)$$$. Now we will prove that $$$n \le f(n)$$$.
We will show it is impossible to solve the problem for any $$$n$$$ with only $$$n - 1$$$ queries. We will show that the grader always has a strategy of answering queries, such that there exists at least 2 different assignments of roles that are consistent with the answers given, and have different nodes as the impostor.
Consider the directed graph generated from the queries. By pigeonhole principle at least one node has in-degree $$$0$$$, and at least one node has out-degree $$$0$$$.
If those two nodes are different, call $$$A$$$ the node with in-degree $$$0$$$ and $$$B$$$ the node with out-degree $$$0$$$. Let the grader always reply yes to your queries.
- $$$A$$$ can be the impostor and everyone else Knaves.
- $$$B$$$ can be the impostor and everyone else Knights.
If those two nodes are the same, then the graph looks like a collection of cycles and one isolated node. The grader will always reply yes except for the last query where it replies no. Let the last query be to player $$$A$$$ about player $$$B$$$. The two assignments of roles are:
- $$$A$$$ is the impostor and everyone else in the cycle is a Knight.
- $$$B$$$ is the impostor and everyone else in the cycle is a Knave.
Thus, we have shown that regardless what the questions asked are, it is impossible to find the impostor among $$$n$$$ players, in $$$n - 1$$$ queries. $$$\blacksquare$$$
Now, we prove that $$$f(3) = 4$$$:
Stare at this image:

lol,
Actually, one of the testers coded the exhaustive checker. I will let them post their code if they want to.
#include <bits/stdc++.h>
using namespace std;
int n;
void answer (int a) {
cout << "! " << a << endl;
}
int query (int a, int b) {
cout << "? " << a << " " << b << endl;
int r;
cin >> r;
if (r == -1)
exit(0);
return r;
}
void main_ () {
cin >> n;
if (n == -1)
exit(0);
if (n == 3) {
if (query(1, 2) != query(2, 1)) {
if (query(1, 3) != query(3, 1)) {
answer(1);
} else {
answer(2);
}
} else {
answer(3);
}
return;
}
for (int i = 1; i + 1 <= n; i += 2) {
if (n % 2 == 1 && i == n - 4)
break;
if ((n % 2 == 0 && i + 1 == n) || query(i, i + 1) != query(i + 1, i)) {
int k = 1;
while (k == i || k == i + 1)
k++;
if (query(i, k) != query(k, i)) {
return answer(i);
} else {
return answer(i + 1);
}
}
}
vector<int> v = {
query(n - 4, n - 3),
query(n - 3, n - 2),
query(n - 2, n - 4)
};
if ((v[0] + v[1] + v[2]) % 2 == 0) {
if (query(n - 3, n - 4) != v[0]) {
if (query(n - 2, n - 3) != v[1]) {
answer(n - 3);
} else {
answer(n - 4);
}
} else {
answer(n - 2);
}
} else {
if (query(n, 1) != query(1, n)) {
answer(n);
} else {
answer(n - 1);
}
}
}
int main () {
int t;
cin >> t;
while (t--)
main_();
return 0;
}
In the Olympiad version, the impostor behaved differently. It could either disguise as a Knight while secretly being a Knave, or disguise as a Knave while secretly being a Knight. Turns out the test cases and the interactor in both versions are practically the same. Why would that be?
Do small cases! Let the pencil (or the computer) do the work and use your brain to look out for patterns.
Try to find the most natural and simple way of modeling the problem.
Learn how to code a decision tree, or other models to exhaustively search for constructions, proof patterns, recursive complete search, etc. and build intuition on that to solve the more general cases of the problem.
2022E1 - Billetes MX (Easy Version)
Consider the extremal cases, what is the answer if the grid is empty? What is the answer if the grid is full? What happens if $$$N = 2$$$?
Observe that if $$$N = 2$$$, the xor of every column is constant. Can we generalize this idea?
Imagine you have a valid full grid $$$a$$$. For each $$$i$$$, change $$$a[0][i]$$$ to $$$a[0][0]\oplus a[0][i]$$$. Observe that the grid still satisfies the condition!
Using the previous idea we can show that for any valid grid, there must exist two arrays $$$X$$$ and $$$Y$$$, such that $$$a[i][j] = X[i] \oplus Y[j]$$$.
Consider doing the operation described in hint 4 for every row and every column of a full grid that satisfies the condition;
- That is, for each row, and each column, fix the first element, and change every value in that row or column by their xor with the first element.
We will be left with a grid whose first row and first column are all zeros.
But this grid also satisfies the condition! So it must hold that $$$a[i][j] \oplus a[i][0] \oplus a[0][j] \oplus a[0][0] = 0$$$, but 3 of this values are zero!
We can conclude that $$$a[i][j]$$$ must also be zero. This shows that there must exist two arrays $$$X$$$ and $$$Y$$$, such that $$$a[i][j] = X[i] \oplus Y[j]$$$, for any valid full grid.
Think of each tile of the grid that we know of, as imposing a condition between two elements of arrays $$$X$$$ and $$$Y$$$. For each tile added, we lose one degree of freedom right? We could make a bunch of substitutions to determine new values of the grid. How can we best model the problem now?
Think about it as a graph where the nodes are rows and columns, and there is an edge between row $$$i$$$ and column $$$j$$$ with weight $$$a[i][j]$$$. Substitutions are now just paths on the graph. If we have a path between the node that represents row $$$i$$$ and column $$$j$$$, the xor of the weights in this path represents the value of $$$a[i][j]$$$. What happens if there's more than one path, and two paths have different values?
To continue hint 7, we can deduce that if there is a cycle with xor of weights distinct to $$$0$$$ in this graph, there would be a contradiction, and arrays $$$X$$$ and $$$Y$$$ can't exist. How can we check if this is the case?
Do a dfs on this graph, maintaining an array $$$p$$$, such that $$$p[u]$$$ is the xor of all edges in the path you took from the root, to node $$$u$$$. Whenever you encounter a back edge between nodes $$$u$$$ and $$$v$$$ with weight $$$w$$$, check if $$$p[u] \oplus p[v] = w$$$.
So lets assume there is no contradiction, ie, all cycles have xor 0. What would be the answer to the problem? We know that if the graph is connected, there exists a path between any two tiles and all the values of the tiles would be determined. So, in how many ways can we make a graph connected?
Say there are $$$K$$$ connected components. We can connect them all using $$$K - 1$$$ edges. For each edge, there are $$$2^{30}$$$ possible values they can have. Thus, the number of ways of making the graph connected is $$$\left(2^{30} \right)^{K - 1}$$$.
Why is this the answer to the problem?
This is just the solution. Please read the hints in order to understand why it works and how to derive it.
Precompute an array $$$c$$$, with $$$c[i] = 2^{30\cdot i} \pmod{10^9 + 7}$$$.
Let $$$a$$$ be the 2d array with known values of the grid. Consider the graph formed by adding an edge between node $$$i$$$ and node $$$j + n$$$ and weight $$$a[i][j]$$$ for every known tile $$$(i, j)$$$ in the grid. Iterate from $$$1$$$ to $$$n + m$$$ maintaining an array $$$p$$$ initialized in $$$-1$$$s. If the current proceed node hasn't been visited, we run a dfs through it. We will use array $$$p$$$ to maintain the running xor for each node during the dfs. If we ever encounter a back edge between nodes $$$u, v$$$ and weight $$$w$$$, we check if $$$p[u] \oplus p[v] = w$$$. If not, we the answer is zero. If this condition always holds, let $$$K$$$ be the number of times you had to run the dfs. $$$K$$$ is also the number of connected components in the graph. The answer is $$$c[K - 1]$$$.
Complexity: $$$\mathcal{O}(n + m + k)$$$.
#include <bits/stdc++.h>
using namespace std;
int const Mxn = 2e5 + 2;
long long int const MOD = 1e9 + 7;
long long int precalc[Mxn];
vector<vector<array<int, 2>>> adj;
bool valid = 1;
int pref[Mxn];
void dfs(int node) {
for (auto [child, w] : adj[node]) {
if (pref[child] == -1) {
pref[child] = pref[node]^w;
dfs(child);
} else {
if ((pref[child]^pref[node]) != w) valid = 0;
}
}
}
int main() {
precalc[0] = 1;
for (int i = 1; i < Mxn; i++) {
precalc[i] = (precalc[i - 1]<<30)%MOD;
}
int tt;
for (cin >> tt; tt; --tt) {
int N, M, K, Q;
cin >> N >> M >> K >> Q;
adj.clear();
adj.assign(N + M, vector<array<int, 2>>{});
int x, y, z;
for (int i = 0; i < K; i++) {
cin >> x >> y >> z;
x--, y--;
adj[x].push_back({y + N, z});
adj[y + N].push_back({x, z});
}
for (int i = 0; i < N + M; i++) pref[i] = -1;
valid = 1;
int cnt = 0;
for (int i = 0; i < N + M; i++) {
if (pref[i] != -1) continue;
cnt++; pref[i] = 0; dfs(i);
}
if (valid) cout << precalc[cnt - 1] << '\n';
else cout << 0 << '\n';
}
}
2022E2 - Billetes MX (Hard Version)
Please read the solution to E1 beforehand, as well as all the hints.
Through the observations in E1, we can reduce the problem to the following: We have a graph, we add edges, and we want to determine after each addition if all its cycles have xor 0, and the number of connected components in the graph.
The edges are never removed, so whenever an edge is added that creates a cycle with xor distinct to zero, this cycle will stay in the graph for all following updates. So we can binary search the first addition that creates a cycle with xor distinct to zero, using the same dfs we used in E1. After the first such edge, the answer will always be zero.
Now, for all the additions before that, we must determine how many connected components the graph has at each step. But this is easily solvable with Disjoint Set Union.
Complexity: $$$\mathcal{O}(\log(q)(n + m + k + q) + \alpha(n + m)(q + k))$$$.
We will answer the queries online. Remember that if the graph only contains cycles with xor $$$0$$$, the xor of a path between a pair of nodes is unique. We'll use this in our advantage. Let $$$W(u, v)$$$ be the unique value of the xor of a path between nodes $$$u$$$ and $$$v$$$.
Lets modify a dsu, drop the path compression, and define array $$$p$$$, that maintains the following invariant:
For every node $$$u$$$ in a component with root $$$r$$$, $$$W(u, r)$$$ equals the xor of $$$p[x]$$$ for all ancestors $$$x$$$ of $$$u$$$ in our dsu (we also consider $$$u$$$ an ancestor of itself).
Whenever we add an edge between two nodes $$$u$$$ and $$$v$$$ in two different components with weight $$$w$$$, we consider consider the roots $$$U$$$ and $$$V$$$ of their respective components. Without loss of generality, assume $$$U$$$'s component has more elements than $$$V$$$'s. We will add an edge with weight $$$W(u, U) \oplus W(v, V) \oplus w$$$ between $$$V$$$ and $$$U$$$, and make $$$U$$$ the root of our new component.
This last step is the small to large optimization, to ensure the height of our trees is logarithmic.
With this data structure, we can maintain the number of connected components like in a usual dsu, and whenever an edge $$$(u, v)$$$ with weight $$$w$$$ is added, and $$$u$$$ and $$$v$$$ belong to the same component, we can obtain the value of $$$W(u, v)$$$ in $$$\mathcal{O(\log(n))}$$$, and check if it is equal to $$$w$$$.
This idea is similar to the data structure described here, and is useful in other contexts.
Complexity: $$$\mathcal{O}(\log(q + k)(n + m + k + q))$$$.
#include <bits/stdc++.h>
using namespace std;
int const Mxn = 2e5 + 2;
long long int const MOD = 1e9 + 7;
vector<vector<array<int, 2>>> adj;
vector<array<int, 3>> Edges;
long long int precalc[Mxn];
struct DSU {
vector<int> leader;
vector<int> sz;
int components;
DSU(int N) {
leader.resize(N); iota(leader.begin(), leader.end(), 0);
sz.assign(N, 1);
components = N;
}
int find(int x) {
return (leader[x] == x) ? x : (leader[x] = find(leader[x]));
}
void unite(int x, int y) {
x = find(x), y = find(y);
if (x == y) return;
if (sz[x] < sz[y]) swap(x, y);
leader[y] = leader[x]; sz[x] += sz[y];
components--;
}
};
bool valid = 1;
int pref[Mxn];
void dfs(int node = 0) {
for (auto [child, w] : adj[node]) {
if (pref[child] == -1) {
pref[child] = pref[node]^w;
dfs(child);
} else {
if ((pref[child]^pref[node]) != w) valid = 0;
}
}
}
int main() {
precalc[0] = 1;
for (int i = 1; i < Mxn; i++) {
precalc[i] = (precalc[i - 1]<<30)%MOD;
}
int tt;
for (cin >> tt; tt; --tt) {
int N, M, K, Q;
cin >> N >> M >> K >> Q;
Edges.clear();
adj.clear();
adj.assign(N + M, vector<array<int, 2>>{});
DSU dsu(N + M);
dsu.components = N + M;
int x, y, z;
for (int i = 0; i < K; i++) {
cin >> x >> y >> z;
x--, y--;
adj[x].push_back({y + N, z});
adj[y + N].push_back({x, z});
dsu.unite(x, y + N);
}
for (int i = 0; i < Q; i++) {
cin >> x >> y >> z;
x--, y--;
Edges.push_back({x, y + N, z});
}
int firstzero = 0;
for (int k = 20; k >= 0; k--) {
if (firstzero + (1<<k) > Q) continue;
for (int i = firstzero; i < firstzero + (1<<k); i++) {
x = Edges[i][0], y = Edges[i][1], z = Edges[i][2];
adj[x].push_back({y, z});
adj[y].push_back({x, z});
}
valid = 1;
for (int i = 0; i < N + M; i++) pref[i] = -1;
for (int i = 0; i < N + M; i++) {
if (pref[i] == -1) pref[i] = 0, dfs(i);
}
if (!valid) {
for (int i = firstzero + (1<<k) - 1; i >= firstzero; --i) {
x = Edges[i][0], y = Edges[i][1];
adj[x].pop_back();
adj[y].pop_back();
}
} else {
firstzero += (1<<k);
}
}
if (firstzero == 0) {
valid = 1;
for (int i = 0; i < N + M; i++) pref[i] = -1;
for (int i = 0; i < N + M; i++) {
if (pref[i] == -1) pref[i] = 0, dfs(i);
}
if (!valid) firstzero--;
}
for (int i = 0; i <= Q; i++) {
if (i <= firstzero) cout << precalc[dsu.components - 1] << '\n';
else cout << 0 << '\n';
if (i == Q) break;
x = Edges[i][0], y = Edges[i][1];
dsu.unite(x, y);
}
}
}
In our Olympiad, we had $$$v_i \le 1$$$ instead of $$$v_i \le 2^{30}$$$, and we also had a final subtask were tiles could change values. How would you solve this?
We have three different solutions for this problem, one of them found during the Olympiad! I'll let the contestant who found it post it if he wants to.
You can model a grid as a bipartite graph between rows and columns.
Whenever coding or designing a data structure, keep in mind all the invariants you are maintaining. I like to think of data structures as graphs with invariants or monovariants in each node. I have a blog draft on how to use this to design data structures, inspired by this. Maybe I will publish it.










The solution code for Problem C shows "you are not allowed to view this page" error. If it opens for anyone, can they share the code in comments!
I'm fixing it. Thanks for let us know
Ready!
How to use B's Alternative Solution(binary search) to solve this problem?
The one I saw consisted in simulating the construction presented in the formal proof (just that W=value_being_processed_in_the_binary_search) making sure you don't sell two cars of the same model to the same customer and that all the cars will be sold.
I love this key takeaways thing
For E1/E2 about checking the validity of the grid , why is the following statement true.
We can deduce that if there is a cycle with xor of weights distinct to 0 in this graph, there would be a contradiction, and arrays X and Y can't existCycle in this graph looks like this r1-c1-r2-c2-r1,we know that each edge has a weight equal to value of ricj(connecting edge i-j). Let's see what will be the cells in the grid are in this cycle => r1c1 , r2c1 , r2c2 , r1c2 , This actually corresponds to a rectangle in the grid, and we know the xor of corners must be zero , so any cycle must have a zero (path)xor for there not to exist any contradiction.
Update :)
R1 — C1 — R2 — C2 — R3 — C3 — R1 => should be zero (This is not a rectangle anymore)
Proof ( if i am not wrong ) :-
Instead of going directly from C2 to R3 , we can go from C2 — R1 — C2 — R3 (path xor from C2 to R3 remains same , as C2 to R1 and R1 to C2 cancels off).
R1 — C1 — R2 — C2 — R1 — C2 — R3 — C3 — R1 now dividing above path to two parts
R1 — C1 — R2 — C2 — R1 (this is a rectangle , so must be 0 path xor) R1 — C2 — R3 — C3 — R1 (same as above)
0^0 = 0
So any cycle can be broken down into multiple rectangles , and we know xor of each rectangle must be zero , so xor of any number of rectangles should be zero.
Meaning a cycle should have zero xor.
yeah that is true , but the thing that confused my mind was , you can still get a cycle in the graph without having any rectangles in the grid. For example :
0011
0110
1100
1001
(0 = unassigned cells , 1 = assigned cells)
In this grid there is no rectangle , however if you plot the graph you would see all edges form a big cycle. So that means XOR of them should be 0. But why is that ?
Yes you have a valid point and I am as much as confused as you are right now! This is just indicating that I haven't understood that the concept utilized clearly:(
Let's say Row vertices are Ri,column vertices are Ci, now in which ever path we go from Ri to Rj the xor of path is always same, provable with some case work and it is exactly equal to Ri^Rj, Same holds for Columns, now when a cycle is formed it is either Ri to Ri or Ci to Ci , now if the grid is valid, path xor must be equal to Ri^Ri , which is indeed zero.
Update :)
R1 — C1 — R2 — C2 — R3 — C3 — R1 => should be zero (This is not a rectangle anymore)
Proof ( if i am not wrong ) :-
Instead of going directly from C2 to R3 , we can go from C2 — R1 — C2 — R3 (path xor from C2 to R3 remains same , as C2 to R1 and R1 to C2 cancels off).
R1 — C1 — R2 — C2 — R1 — C2 — R3 — C3 — R1 now dividing above path to two parts
R1 — C1 — R2 — C2 — R1 (this is a rectangle , so must be 0 path xor) R1 — C2 — R3 — C3 — R1 (same as above)
0^0 = 0
So any cycle can be broken down into multiple rectangles , and we know xor of each rectangle must be zero , so xor of any number of rectangles should be zero.
Meaning a cycle should have zero xor.
I see , when you rephrase the problem as "can you get any bipartite cycles with xoring a bunch of 4 length bipartite cycles" it suddenly seemed much more reasonable. Playing with the cases , it is easy to realize you can get any length cycles by adding the 4 length cycles next to each other and then when you have the same length you just order the nodes to get the desired cycle. This makes so much sense , Thx for the help.
Why this greedy approach for Problem-B gives WA on test2. 285737349
(Copy and pasted from a message I sent in discord)
The code fails on the following test (example)
1 3 2 4 4 3
Optimal strategy: Get 3 customers to purchase cars 1 and 2: 1 1 3 Get 1 customer to purchase cars 2 and 3: 1 0 2 Get 1 customer to purchase cars 1 and 3: 0 0 1 Get 1 customer to purchase car 3: 0 0 0
Thanks, I was breaking my head for 2 hours. Took a break and while walking read your comment. I missed it earlier somehow : lol
You're not alone on that, I also spent the entire contest trying to use greedy and I couldn't figure out why it didn't work :(.
nik_exists could you please tell how u found this test case where it was failing ?
This was an example test case where your code went wrong, I don't know if this exact test case is in the system tests (though I'd say it's fairly likely that something like this is there), I simply ran a test case generator and compared the answers of the correct solution to the greedy solution.
where did you find the test case generator ? U wrote it ?
Yep, wrote it myself, here's the code if you are interested (outputs the input first, then the expected output second so I can easily put it into CPH)
Thanks a ton for your help. I didn't even know about the CPH extension on vs code. I just downloaded it, and it's gonna help a lot.
285980247
Why it is giving WA on test case 2. For Problem B
https://codeforces.net/blog/entry/134997?#comment-1208085
Thanks!
In D1, We know that if ask(i,j)!=ask(j,i) then one of them must be the impostor, However, I'm slightly confused as I queried on pairs that are distinct (i.e 1,n 2,n-1 and so on). Since the grader was adaptive, I declared j as impostor if ask(i,j)!=ask(j,i), since it's possible for any of them to be the impostor and since the queries are independent of the previous ones.
Why do we need to verify again which one is the impostor once we get the above condition?
if query(i,j)!=query(j,i) happens than it is guranted that other than i and j all people are genuine (no one is imposter) so what you can do is query any of other person with either i or j ,suppose u did it with i and result comes same for both(i ,other and other,i) than j would be imposter and i result comes out to be different than i would be imposter .... since n>=3 so answer will always be possible in atmost n+1 queries
See, according to the question, the grader is adaptive (the fixed order isn't decided beforehand) ,so isn't it so that I can claim any one of them to be the impostor and still the answer would be correct?
i don't think that's correct i believe that there is equal probability that any of two could be imposter, so u would have to confirm among them rather than assuming , you should focus on this line "However, it is guaranteed that there exists an assignment of roles that is consistent with all previously asked questions under the constraints of this problem"
Yes, my assumption goes in line with the statement! "There exists an assignment of roles that is consistent with all the PREVIOUSLY ASKED questions". Since the previously asked questions were all on entirely different pairs, we haven't eliminated any of the elements from the currently-being-tested pair from the possibility of being the impostor, as all the queries (1,n) (2,n-1) (3,n-2)... are independent of each other.
Hence my assumption lies in line with the consistency of data on previously asked questions. JuanPabloAmezcua correct me if I am wrong.
ok suppose that after you considered any one as imposter out of two(let u consider u as imposter btw u and v) and you ask one more query (u,1 and 1,u) i am considering that 1 and n query is safe, which means 1,n gave same results for 1,n and n,1. If 1 and u gives same for both (u,1)and (1,u) dosen't this disapproves the assumption which we made earlier that u is imposter and are all the queries still consistent? the answer is no so we do have to verify once again with any other element .sorry for bad English.
Your assumption doesn't work because your guess being consistent with all the previous answers is necessary, not sufficient. According to your (very stupid) logic, you could just guess at the start who the impostor is, since technically you didn't ask anything, and it could techinically be anyone.
Ahh now that you say it, indeed it's very stupid of me to think so.
I get that. Thanks
B was same as this Codechef Problem lol
I have seen it atleast 3 times now, and x <= 10 is a bit misleading towards a dp approach :(
I think B is a well known problem, I have solved this problem (or some more difficult variant) at least 5 times.
Hi can you refer me to these more difficult variant
can you refer some of the problem?
Great way of writing Editorial
errorgorn beautiful proof for B! I've been thinking for 3 days straight to solve it and never succeeded, but I don't feel sad bc I'm so inspired by your solution!
BTW, key takeaway for B is hilarious cuz trying to find the pattern in small cases for this particular problem will take you in the wrong direction with 99% probability.
the contest was near to shit for me :)
but the editorial is one of the best ones.
Can you explain to me how you came up with the solution for B during the contest? What was the way of thinking, why did you decide to give your solution a try and did you prove to yourself that it would pass all tests?
Thanks in advance.
I guessed the awnser. getting AC was the proof
Based.
first i noticed that the answer is atleast MAX number of the array.
then i tried to make examples that the answer is more then the MAX. after few examples i found that the answer is ceil(SUM / x) and is worked for the samples and i submitted the code
If someone is looking for a BS(binary search) solution for B then here it is
https://codeforces.net/contest/2022/submission/286452965
Why this approach of choosing the top x models with maximum left cars every time doesn't work?
... ~~~~~ void solve() { int t = 1; cin >> t;
while (t--) { int n, x; cin>>n>>x; vector<int>v(n); for(int i = 0; i < n; i++)cin>>v[i]; priority_queue<pi>pq; for(int i = 0; i < n; i++)pq.push({v[i], i}); int ans = 0; vector<pi>ti; while(!pq.empty()) { for(int j = 0; j < x && !pq.empty(); j++) { ti.push_back(pq.top());pq.pop(); } if(ti.size() == 0)continue; ans += ti[ti.size() - 1].first; int z = ti[ti.size() - 1].first; int ad = z; for(int i = ti.size() - 1; i >= 0; i--) { ti[i].first -= z; if(ti[i].first > 0)pq.push(ti[i]); ti.pop_back(); } } cout<<ans<<endl; }undef int
~~~~~
why my sol for D1 is giving wrong output format Unexpected end of file — token expected
submission link:check out
It was really beautiful! Thank you.
Since when was broken profile dp div2.C material
Doesn't the provided solution for problem B fail for test cases like n=4,x=3, with car models [1,1,1,3]?
The code calculates the answer as 3, but the correct value is 4. Am I missing something, or is there an issue with the logic in the solution?
The correct value is not 4...
A less troublesome way to solve C may be just using the naive DP definition. $$$dp(i, j)$$$ for answer given prefix to $$$i$$$ of the top row and prefix to $$$j$$$ of the bottom row. If implemented using recursion the transitions are simple to see. And it may quickly be optimized to linear time by recognizing any state with $$$|i-j|>3$$$ is redundant.
for B can anybody check for test case - 3 2 - 9 8 5