Это русский разбор задач D, E и F.

D — Дерево с ограничениями

Будем строить дерево сверху вниз, пытаясь выполнять данные ограничения. Можно заметить, что если вершины i и j (i < j) должны быть в некотором поддереве, то любая вершина k (i < k < j) также должна быть в этом поддереве. Из этого следует два вывода:

1. Задачу "найдите дерево с корнем 1, которое будет иметь N вершин и для которого выполняются данные ограничения" можно переформулировать как "найдите дерево с корнем 1, для которого выполняются данные ограничения, которое должно содержать как можно меньше вершин и которое содержит вершину N"
2. Нам нужно знать только минимумы и максимумы для левых и правых частей каждого поддерева.

Пусть, мы пытаемся построить поддерево с корнем i, которое должно содержать вершину m, вершины [j₁..j₂] слева от корня и вершины [k₁..k₂] справа от корня. Если ограничения для левой или правой части поддерева отсутствуют, то мы можем поместить все вершины полностью направо или полностью налево (мы все равно должны проверить выполнение имеющихся ограничений). В противном случае должно выполняться i < j₁, j₂ < k₁. Левый ребенок корня должен быть вершиной i + 1. Вершины [j₂ + 1;k₁ - 1] могут располагаться слева или справа от корня. Построим левое поддерево с корнем i + 1 так, чтобы оно содержало вершину j₂ и имело как можно меньше вершин. Пусть, вершина с наибольшим номером в этом поддереве mid. Тогда должно выполняться условие mid < k₁. Можно сделать так, чтобы правый ребенок имел индекс mid + 1, и нам осталось построить правое поддерево так, чтобы в нем обязательно была вершина max(k₂, m).

Сложность алгоритма O(N + C)

E — Разрезание массива

В общем случае нам нужно вычислить следующее выражение:

max(... + |s_j - 2 - s_j - 1| + |s_j - 1 - s_j| + |s_j - s_j + 1| + ...) = max(... ± (s_j - 2 - s_j - 1) ± (s_j - 1 - s_j) ± (s_j - s_j + 1) ± ...)

Эта задача может быть решена с помощью динамического программирования. Будем рекуррентно считать следующую функцию, в которой нам нужно выбрать подмассивы j..k из массива [i; n]:

f(i, j, c₁, c₂) = max(... ± (0 - 0) c₁ (0 - s_j) c₂ (s_j - s_j + 1) ± (s_j + 1 - s_j + 2) ± ...), где 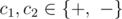заданы.

Рекуррентная формула для этой функции:

f(i, j, c₁, c₂) = max_p1, p2(c₁ ( - sum_{p = p1..p2}a_p) c₂ (sum_{p = p1..p2}a_p) + f(p₂ + 1, j + 1, c₂,  ± ))

Мы легко можем избавиться от p₁:

f(i, j, c₁, c₂) = max(f(i + 1, j, c₁, c₂), max_p2(c₁ ( - sum_{p = i..p2}a_p) c₂ (sum_{p = i..p2}a_p) + f(p₂ + 1, j + 1, c₂,  ± ))

Мы можем избавиться от p₂ используя дополнительную функцию g(i, j, c₁, c₂), означающую, что в подмассиве j уже есть некоторые элементы:

f(i, j, c₁, c₂) = max(f(i + 1, j, c₁, c₂), c₁ ( - a_i) c₂ a_i + g(i + 1, j, c₁, c₂))

g(i, j, c₁, c₂) = max(f(i, j + 1, c₂,  + ), f(i, j + 1, c₂,  - ), c₁ ( - a_i) c₂ (a_i) + g(i + 1, j, c₁, c₂))

Осталось разобраться с началом и окончанием динамического программирования. Есть несколько способов это сделать. Например, мы можем посчитать максимумы и минимумы значений s₁ или s_k в зависимости от их концов или начал, или мы можем сделать исключения для использования c₁ and c₂ если j = 1 или j = k.

Сложность алгоритма O(n * k)

F — Скейгербосс

Задача сводится к тому, что у нас есть k женских особей и k мужских особей, и нам надо их соединить так, чтобы в одной клетке было не больше пары. Задача решается потоком.

Будем перебирать ответ к задачи ans (например, двоичным поиском). Проведем единичные ребра от истока к женским особям и от мужских особей к вытоку. Проведем единичные ребра от входа до выхода каждой клетки. И проведем единичные ребра от женских особей к входам каждой клетки, если она может туда дойти не больше, чем за ans. Аналогично проведем единичные ребра от выходов каждой клетки до мужских особей. Ответ не больше ans если в таком графе существует поток размером k.

Описанный выше подход достаточен, чтобы решить первую часть задачи. Сложность алгоритма O(k³ * log(k)). Для решения второй части задачи нужно оптимизировать данное решение. Хорошо соптимизированное решение с данной сложностью может пройти по TL, но существует решение со сложностью O(k³).

Можно заметить, что вам не надо перестраивать граф каждый раз для запуска потока. Если вы запускаете поток для ans = a, а затем запускаете поток для ans = b, b > a, вы можете просто добавить недостающие ребра и "продолжить работу" потока. Сложность этого подхода O(k³ + l * k²) где l — количество раз, вы будете производить этот трюк. Использование такого наблюдения разными способами должно быть достаточно для сдачи второй части задачи.

Вы можете достичь чистой сложности O(k³) используя корневую декомпозицию. Вы можете разделить k² ребер на k групп по k ребер в зависимости от значений ans, для которых можно использовать эти ребра. Запуская поток после добавления каждой группы ребер вы получите сложность O(k³). Затем вы знаете, какую группу ребер нужно изучать для нахождения ответа и, запуская поток после добавления ребер этой группы, вы получаете снова сложность O(k³).

Вы также можете поделить ребра на группы в зависимости от их длин (потраченного времени), а не в зависимости от их количества. Вам нужно будет добавлять ребра одинаковой длины одновременно. Так можно еще больше ускорить работу алгоритма.

Я (White_Bear) хотел бы передать особенные поздравления mmaxio, Petr, niyaznigmatul и Egor, которые решили F2 на Java.

Автором задач четвертьфиналов Украины (которые также были задачами командного турнира Открытого кубка ДонНУ) был я. Редактированием и переводом условий также занималисть Антон Парамонов и Виталий Бондаренко (вероятно еще кто-то, не в курсе всего процесса).

Задачи были доступны в английском и украинском вариантах. В тренировке также есть русский вариант

Problem A. Game

Для начала определим проигрышность или выигрышность одного регистра. Она зависит от остатка деления числа на 5

0, 1: проигрышная позиция

2: 3: выигрышная позиция 1 типа

4: выигрышная позиция 2 типа

Далее считаем количество выигрышных позиций обоего типа в игре. Если оба числа — четные, то ситуация проигрышная, иначе — выигрышная

См. функцию Шпрага-Гранди для лучшего понимания

Problem B. Watson’s memory

Заметим, что 16 mod 7 = 2

Тогда число из единиц делится на 7, если делится на 7 число 1 + 2 + 4 + 1 + 2 + 4 + 1 +... (продолжительность — количество цифр)

Видно, что это число будет делится на 7, когда количество цифр будет делится на 3

Чтобы определить делимость на 3 входного числа, надо сложить все его цифры и поделить на 3

Problem C. Accomodation

Нужна структура данных для быстрого ответа на запросы

По сути достаточно 2 set-ов — один для хранения занятых мест, другой для хранения свободных отрезков (вида пары значений <длина отрезка> — <позиция>)

При поступлении анализируем, какое место лучше взять — начало, конец или середина самого большого отрезка

Problem D. Work

Задачу можно решать намного проще авторского решения

Мое решение было таким:

Решим сначала задачу для n, m < 1000

Построим такое дп

f(i, j) — существует ли такая выборка из чисел i..n, что последовательность простых-непростых в ней j..m

p[i] — простота i-го числа

s[i] — простота i-го числа в заданной последовательности

f(i, j) = p[i] == s[j] ? f(i + 1, j + 1) : f(i + 1, j)

Мы определяем уникальность каждого числа при вычислениях в дп. Каждое число мы помечаем одним из состояний: не найдено; найдено и равно x; возможны разные значения. Эти состояния помечаем при проверке p[i] == s[j], если при этом выполняется f(i + 1, j + 1), попутно проверяем другие возможности (f(i + 1, j))

Теперь для n, m < 3 * 10^4

Вместо последовательностей <простое или непростое число> будем работать с последовательностями <количество непростых чисел> — <простое число>. Так мы сокращаем количество элементов до количества простых чисел. В задаче был низкий ML 16Мб.

Тогда наше новое дп:

f(i, j) — существует ли такая выборка из чисел (i-е простое число)..n, что последовательность простых-непростых в ней (j-е простое число в заданной последовательности)..m

f(i, j) = f(i + l, j + 1)

Параметр l — сколько нам нужно блоков в последовательности (i-е простое число)..n, чтобы покрыть текущий блок в заданной последовательности. Его можно находить бинарным поиском или другим методом

Также при выполнении f(i + l, j + 1) проверяем другие возможности и меняем состояния чисел (а точнее блоков чисел)

Сложность алгоритма O(N * M / log(M)), потребляемая память O(N * M / log(N) / log(M)).

Problem E. Construction

Решается таким дп:

f(i) = max(f(i + m), a[i] + a[i + m] + f(i + 2 * m));

ответ — сумма f(i) от 0 до m — 1

Problem F. Task

Работа с длинными числами в этой задачи не требуется, можно избежать любых переполнений.

Нужно вычислить f(n, a) + f(n, b) — f(n, lcm(a, b)) mod 1000000007. При этом нужно избежать переполнения. Заметим, что при n / (a / gcd(a, b)) < b вычислять третий член не нужно

f(n, a) = asum(n / a) * a, где asum — сумма арифметической прогрессии

asum(n) = (1 + n) * n / 2. Одно число из множителей в числителе будет четным, делим его на 2, потом берем по модулю все слагаемые и перемножаем их

Problem G. Palindrome

Решается перебором всех возжожных множителей

Problem H. Control chain

Задача была сложна для понимания. Я попробую ее кратко переформулировать

Есть страна в виде взвешенного дерева (вес дерева — длина дороги). Каждый город ходил армией на каждый другой город. После всех походов каждый город посадил дерево на дороге (-ах), где его армия провела наибольшее количество времени. Найти количество деревьев на самой красивой дороге

Нужно несколько раз пройтись поиском в глубину по дереву, вычисляя следующие значения:

1. Количество вершин в поддереве

2. Наибольшая интенсивность (произведение количества вершин в поддереве на длину входящего ребра) в поддереве при поступающем сигнале(армии) сверху

3. Распределяем критичности (деревья) по пути снизу вверх

4. Распределяем критичности (деревья) по пути сверху вниз

Как совершить быстро третий шаг: для каждого узла считаем максимум и второй максимум из интенсивностей (несколько вниз и один вверх). Нам нужно сохранить на ребрах деревья, которые пойдут вниз на 4 шаге. Для каждого ребенка получаем количество дереввьев, идущих снизу и должны их направить по максимуму или второму максимуму (сохраняем это в переменных и вычитаем из значения в текущем ребре если нужно). Затем еще раз проходим по всем выходящим вниз ребрам и прибавляем к ним деревья

В конце считаем максимум из критичностей ребер

Сложность алгоритма O(n)

Problem I. Cube

Нужно получить наименьший по длине путь, а среди них лексиграфически наименьший. Затем вывести часть этого пути

Для начала нам нужно 2 структуры

• одна структура будет осуществлять изменение ориентации куба (я бы хранил три переменных и разобрал отдельно 4 случая — каждый из них занял бы при этом 3 строчки: сохранение промежуточного значения, изменение одной грани на соседнюю, изменение соседней на 5 — <промежуточное значение>)

• путь в виде пар <символ>-<количество символов>

Докажем следующее утверждение: путь будет содержать только один блок однонаправленных элементов по длине больше или равно 4 (в общей сложности таких блоков будет 2 для разных направлений).

4 одинаковые поворота возвращают куб в изначальную ориентацию, значит мы можем этот блок свободно перемещать по пути. Все такие блоки в лексиграфически минимальном пути соберутся в одном месте

Тогда решение: меняем координаты цели на (x + 4p, y + 4q) так, чтобы цель оказалась близко к т. (0, 0). Квадрата 30x30 вокруг (0, 0) достаточно с избытком.

Получаем путь с помощью поиска в ширину из цели в начало (для получения нужного пути из начала в конец). Далее находим блоки из 4 и более элементов и добавляем туда недостающие

Problem J. Duty

Для решения этого задачу нужно понимать задачу Эйлера для мостов

Для начала нам нужно исключить из рассмотрения вершины без выходящих из них дорог. Нам не нужно их посещать

Если у нас осталась одна компонента связности, то ответом будет <количество вершин с нечетными степенями> / 2

Если несколько компонент связности, то мы обязаны их всех соединить между собой, поэтому ответом будет sum(max(2, <количество вершин с нечетными степенями в компоненте>)) / 2

Problem K. Method of linear transformation

Нужно прочитать условие и понять, что нужно просто вывести 0.3989

Problem L. Watson’s magic number

Посчитать детерминант матрицы 3x3

Problem M. Formatting

Перебрать каждую степень 10 отдельно и посчитать количество чисел в диапазоне [a; a + n — 1]

UPD: создал тренировку