Hi Guys,
Hope you enjoyed Round 174. :) I would like to add a few comments on some of the problems, beyond the editorial.
div 2 A ****
If you know some math, you can actually solve this problem in 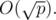 (!!!) You can show that the answer is φ (p - 1) where φ (n) is the number of positive integers i less than to n with gcd(i, n) = 1. To prove this we first show that there is always at least one primitive root
(!!!) You can show that the answer is φ (p - 1) where φ (n) is the number of positive integers i less than to n with gcd(i, n) = 1. To prove this we first show that there is always at least one primitive root 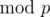 for all primes p. (This is a fairly well known result so I won’t prove it here, but you can find many proofs online) So now assume g is a primitive root
for all primes p. (This is a fairly well known result so I won’t prove it here, but you can find many proofs online) So now assume g is a primitive root 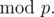 Then, the set {g, g2, ... gp - 1} is congruent to the set {1, 2, ... , p - 1}. Furthermore, its not hard to show that gi is a primitive root if and only if gcd(i, p - 1) = 1, (try it!) hence our formula φ (p - 1). φ (n) can be computed by getting the prime factors of n, since
Then, the set {g, g2, ... gp - 1} is congruent to the set {1, 2, ... , p - 1}. Furthermore, its not hard to show that gi is a primitive root if and only if gcd(i, p - 1) = 1, (try it!) hence our formula φ (p - 1). φ (n) can be computed by getting the prime factors of n, since 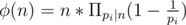 so this gives us our
so this gives us our 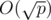 algorithm. :)
algorithm. :)
div 1 D ****
Here is a full solution to Codeforces #174 div 1 D.
Let ν2(n) denote the exponent of the largest power of 2 that divides n. For example ν2(5) = 0, ν2(96) = 5. Let f(n) denote the largest odd factor of n.
Note the following formula for sum of arithmetic series:
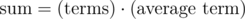
I claim that the pair (x, y) is cool if and only if 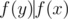 and one of the following is true \begin{enumerate} \item ν2(x) + 1 = ν2(y) \item ν2(y) = 0 \end{enumerate} This can be proven by casework on the number on the parity of y.
and one of the following is true \begin{enumerate} \item ν2(x) + 1 = ν2(y) \item ν2(y) = 0 \end{enumerate} This can be proven by casework on the number on the parity of y.
If y is odd, the average term of the arithmetic sequence is an integer, so f(y) = y divides f(x) and ν2(y) = 0.
If y is even, the average is of the form .5·k where k is odd, so 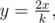 so it follows that y divides x so f(y) divides f(x), and furthermore
so it follows that y divides x so f(y) divides f(x), and furthermore 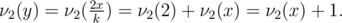
From this observation it follows that for fixed ai, aj(i < j), we can construct a cool sequence ai = bi, bi + 1, ... bj - 1, bj = aj if and only if 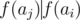 and either ν2(ai) + j - i = ν2(aj) or ν2(aj) ≤ j - i - 1.
and either ν2(ai) + j - i = ν2(aj) or ν2(aj) ≤ j - i - 1.
Now that we have this observation, we can finish the problem using dynamic programming where the kth state is the maximum number of ai (i ≤ k) we can keep so that it is possible to make a1, ... ak cool. Then the answer is just n - max (dp[1], dp[2], ..., dp[n]).
div 1 E ****
Here is a full solution to Codeforces 174 div 1 E. I find this problem beautiful. :)
The first thing to note, is that, if you interpret the problem as a graph, you can compute the answer if you have the degrees (i.e. number of wins) of every cow. Call three cows ``unbalanced’’ if the is one cow that beats the other two. Note that every three cows is either unbalanced or balanced (there are no other configurations of three cows). Thus,
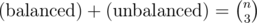
So to count the number of balanced it suffices to count the number of unbalanced. But it is easy to show that 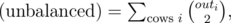 so
so 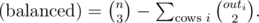
So now we have reduced the problem to computing the number of wins for each cow. If we do this the dumb way, this is O(MN^2), still way too slow.
Sort the skill levels of the cows (the order of the si doesn’t actually matter). s1 is lowest skill Now consider an n × n grid where the ith row and jth column of the grid is a 1 if the match between cow i and cow j is flipped. The grid is initially all zeros and Farmer John’s query simply flips a rectangle of the form [a, b] × [a, b], and the outdegree (#wins) of cow i is just (Number of 1’s in range [1,i — 1]) + (Number of 0’s in range [i + 1, N]) = (Number of 1’s in range [1,i — 1]) + (N — i — (Number of 1’s in range [i + 1, N]))
We can process these queries and compute outdegrees using a sweep line with a seg tree on the interval [1,N]. The seg tree needs to handle queries of the form
Flip all numbers (0->1, 1->0) in a range [a, b].
Query number of 1’s in a range [a, b].
Note that the seg tree needed to handle this is the same seg tree you need for problem ‘lites’ on USACO 2008 Gold http://tjsct.wikidot.com/usaco-nov08-gold.
Once again, thanks for participating!
abacadaea








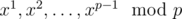 in
in 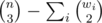 where
where 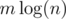 time.
time.
