Motivation problem
We aim to solve this problem: Path Queries 2.
Summary: Given a tree with weighted nodes, you are asked to answer the following type of queries: What is the maximum value on the path connecting nodes A and B ?
Definitions
- A heavy child of a node is the child with the largest subtree size rooted at the child
- A heavy edge connects a node to its heavy child
- A light child of a node is a child that it's not heavy
- A light edge connects a node with a light child
- A heavy path is a path made of heavy edges
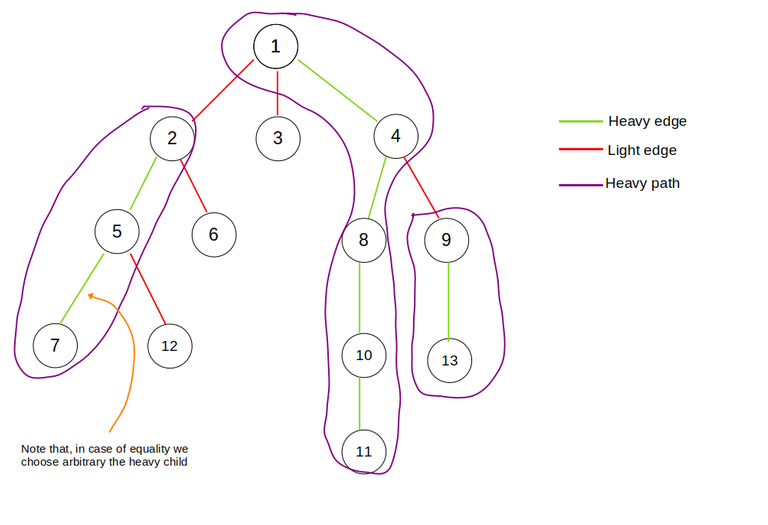
How it works
The main idea is to make use of the heavy paths in answering the queries, so we divide the path in heavy paths contained by it and then we add those heavy paths in a Segment Tree to support maximum-value query.
- Any path from node $$$u$$$ to node $$$v$$$ passes through at most $$$O(log N)$$$ light edges.
1. The first step is to compute every node's subtree size in order to find out the heavy edges.
2. Then we mark the heavy paths and add the nodes in the segment tree. Each heavy-path's nodes form a continuous sequence in the segment tree in order to support queries on a specific heavy-path. As you can see in the image below heavy path's nodes form a contiguous sequence of numbers:
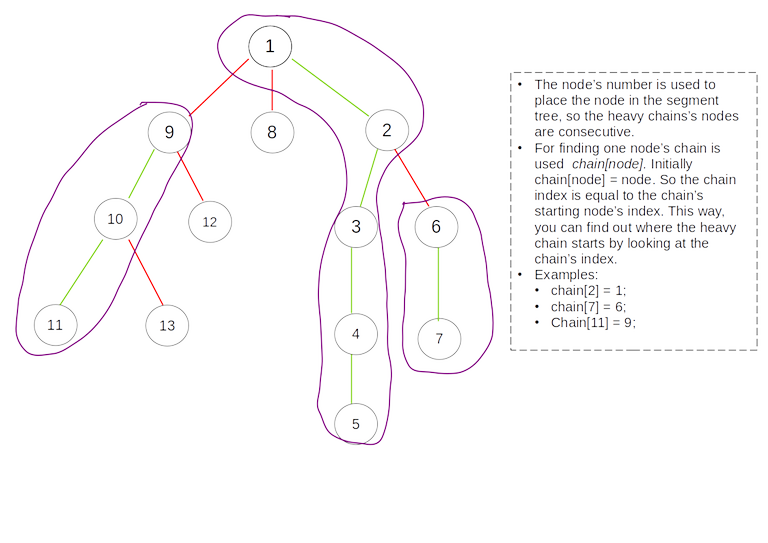
3. The final step is to build the segment tree.
Answering queries
Answering queries can become much easier by dividing the path from node $$$u$$$ to node $$$v$$$ into 2 vertical chains:
- the chain from $$$u$$$ to $$$LCA(u, v)$$$
- the chain from $$$v$$$ to $$$LCA(u, v)$$$
To get the answer for the path combine the 2 answers. Now, answering the query for a vertical chain is pretty much straight forward: Jump through each heavy path contained by the chain and query it using the segment tree. You can think it as binary jumping. Once in the heavy chain, query it, jump to parent of chain's starting node and repeat. 
Source code
you can find the hole code here.










