Я нашел следующее решение с методом множителей Лагранжа задачи Core Training в этом раунде Code Jam. Мне понравилось это решение в частности потому, что в соревнованиях по программированию очень редко встречается задачи со множителями Лагранжа.

Пусть 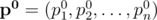-- заданный вектор вероятностей успеха ядр и 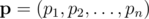-- другой вектор вероятностей. Пусть -- вероятность, что точно i ядр будут успешными, допустя что ядро i будет успешным с вероятностей p_i. Тогда мы хотим найти максимум функции

с ограничением

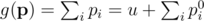
По методу множителей Лагранжа, мы знаем что любой максимум 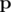должен удовлетворить условию

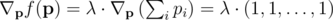
или лежить на границе множества решений (но мы сочтем этот случай попозже).

Лемма

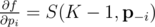
где 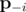-- вектор вероятностей без p_i, т.е. (p₁, p₂, ..., p_i - 1, p_i + 1, ..., p_n). Иными словами, частная производная f по переменной p_i -- это вероятность, что K - 1 других ядр будут успешными (без ядра i).

Доказательство Леммы

Разложим члены уравнения:

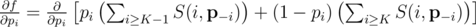
Упростим выражение:

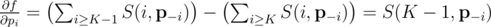
(Конец доказательства.)

Наивное решение 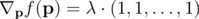-- установить все p_i равные друг друга. Но это невозможно потому, что мы не можем уменьшить p_i меньше чем p⁰_i. С учетом граничных условий, мы имеем для каждого ядра i три вариантов:

1. Оставим p_i как p⁰_i.
2. Увеличим p_i до 1.
3. Установим p_i равные каких-то других {p_j}.

Это наблюдение ограничает множесвто решений до такой степени, что мы можем его перебрать. (Ну, еще нужно несколько оптимизаий, например "увеличить p_i до 1 только если p_i уже велик", но это главная идея.)

Задача A - IQ Тест

Надо просто посчитать количество чётных и нечётных числ. В данных числах может быть или только одно чётное число, или только одно нечётное число --- надо найти его и вывести его номер.

Задача B - Телефонные Номера

Есть много методов разбить на группы из 2 или 3 цифр. Представим один простой вариант: вывести группы из двух цифр пока останется больше чем 3 цифр:

<code>
for( i=0; i<n; i++ )
{
    putchar(buf[i]);
    if( i%2 && i<n-(n%2)-2 ) putchar('-');
}
</code>

Задача C - Дороги в Берляндии

Входнные данные --- матрица D, в которой D[i][j] явлется кратчайшим расстоянием между городами i и j. Если создадим новуюу дорогу между городами a и b с расстоянием меньше чем D[a][b], как обновить остальные расстояния в D?

Пусть матрица D'[i][j] --- кратчайшее расстояние между i и j если добавим в граф новое ребро ab. Для каждой пары вершин i, j есть три возможности:

• D'[i][j] не уменьшивается после добавления новой дороги ab: тогда D'[i][j] = D[i][j]
• D'[i][j] меньше чем D[i][j], если мы используем ab. Тогда новый кратчайший путь i, v₁, v₂, ..., v_n, j включает дорогу a, b. Надо пройти вершины i, a, b, j, в этом порядке --- значит новое расстояние будет D[i][a] + length(ab) + D[b][j].
• D'[i][j] меньше чем D[i][j], если мы используем ab. (Заметим, что это не так же, как использовать ab.) Тогда D'[i][j] = D[i][b] + length(ab) + D[a][j].

Поэтому, для каждой новой дороги надо обновить каждое расстояние i, j в матрице. Тогда надо суммировать все расстояние. Обновить и суммировать --- оба O(N²) или около 300² операций. Максмальное количество дорог --- 300, в итоге операций 300³.

Наконец, надо заметить, что сумма всех расстояние может быть больше чем 2^31, поэтому надо посчитать сумму как 64-битовое целое число.

Задача D - Дороги не только в Берляндии

В решении этой задаче используем структуру данных система непересекающихся множеств. Главная идея: структура данных --- множество элементов x₁, x₂, x₃, ..., x_n с каким-то рабиением, которое поддерживает эти операции:

• найти множество, которому принадлежит элемент x_i
  
• объединить любое два множество
  

Эта структура данных часто появляется в соревнованиях по программированию. Можно писать алгоритм по-разному; вот хороший вариант написан Bruce Merry (BMerry) здесь.

Каждый день можно закрыть одну дорогу и построить одну дорогу. Поэтому, можно разделить решение на две части:

• Как связать несвязные компоненты графа?
  
• Как удалить ненужные ребра, не разъединяя граф?
  

Пусть build - список дорог, которые надо построить, и пусть close - список дорог, которые надо закрыть чтобы построить нужные дороги. Можно доказать, что на самом деле, эти списки одного и того же размера. Это следствие того, что связный граф с n вершинами является деревом тогда и только тогда, когда оно имеет n - 1 ребёр. Поэтому, если закроем больше дорог, чем построим, тогда граф будет несвязный. Наоборот, если построим больше чем закроем тогда будут ненужные ребра (т.е. граф больше не дерево).

Считаем входные данные:
a₁, b₁
a₂, b₂
...
a_n - 1, b_n - 1
Можно доказать, что ребро (a_i, b_i) ненужные тогда и только тогда, когда вершины a_i, b_i уже связаны ребрами (a₁, b₁), (a₂, b₂), ..., (a_i - 1, b_i - 1). Т.е, если a_i, b_i принадлежит одной и той же компоненте связности без ребра (a_i, b_i), тогда не надо добавить (a_i, b_i) в граф. Используется система непересекающихся множеств:

<code>
for( i from 1 to n-1 )
{
    if( find(a_i)=find(b_i) ) close.add(a_i, b_i);
    else merge(a_i, b_i);
}
</code>

Иначе говоря, считаем каждую компоненту связности как множество в разбиении вершин. Структура данных помогает нам найти то, в каком множестве лежат элементы a_i, b_i. Если они в одном множестве, тогда можно закрыть дорогу (a_i, b_i). Если они лежат в других множествах/компонентах, тогда можно объединить эти множества.

Вторая задача - связать несвязные компоненты - тоже решается системой непересекаующихся множеств. Проходим все вершины; когда найдём компоненту несвязную с первой компонентой, тогда добавим ребро между ними.

<code>
for( i from 2 to n )
    if( find(v_i)!=find(v₁) )
    {
        then merge(v₁, v_i);
        build.add(v₁, v_i);
    }
</code>

(Кстати, у меня вопрос --- на русском языке есть соокращение или короче форма "система непересекающихся множеств"? Моим пальцам больно печатать ваши огромные русские фразы =P)

Задача E - Тест

Я решил эту задачу хешированием. Так как в хешированиях могут существовать коллизии, на самом деле моё решение "неправильно", но оно всё равно правильно отвечает на все тесты =P

Пусть входные строки s₀, s₁, s₂. Постараемся найти кратчайшую строку, которая содержит s₀, s₁, s₂. Пройдём все порядки s₀, s₁, s₂ и поищем длинейшее перекрытие в конце строки a и начале строки b. Польный перебор конечно требует слишком много времени. С другой стороны, херширование может решить за O(n) операции, где n = min(len(a), len(b)). Моя хеш-функция - полином hash(x₀, x₁, ..., x_n) = x₀ + ax₁ + a²x₂ + ... + aⁿx_n. Этот полином удобный в этой задаче потому что он имеет следующее свойство:
Если известно hash(x_i, ..., x_j), тогда можно за O(1) посчитать следующие значения:

• hash(x_i - 1, x_i, ..., x_j) = x_i - 1 + a × hash(x_i, ..., x_j)
• hash(x_i, ..., x_j, x_j + 1) = hash(x_i, ..., x_j) + a^{j + 1 - i} × x_j + 1

Т.е., если известно значение хеш-функции какой-то подстроки, легко посчитать значение соседных подстрок. Для строк a, b, посчитаем значения хеш-функций подстрок в конце a и в начале b. Если они равные для подстрок размера n, тогда значит, что (может быть) есть дублирование n характеров в a и b.

Поэтому, пройдём все порядки s₀, s₁, s₂, и попробуем связать строки вместе. Осталась одна проблема --- если s_i подстрока s_j и i ≠ j, тогда можно пропустить s_i. Используем хеширование быстро решить, s_i подстрока s_j или нет.