This post doesn't include a special or creative solution. It's about how to implement the solutions in the editorial. This kind of post is unnecessary for C++ or Java, but it's Haskell and there's no one who completed the round with Haskell ;) I can't assure if my codes are in pure functional way or very efficient, but at least they were accepted. I hope it will be helpful.
734A - Антон и Даник
Take the outcome as a String and count the number of 'A' and 'D' in it. It's very simple problem so I just traversed the string twice (two calls of length . filter.) If you want to do it 2x faster, you can use partition in Data.List.
code: 22282938
734B - Антон и цифры
Another simple problem. Here is the line that reads the input:
[k2, k3, k5, k6] <- (map read . words) `fmap` getLine :: IO [Integer]
If input is small like this, it has no problem. When you have to read a large number of integers, there is two considerations — speed and memory. They'll be examined in later problems.
code: 22282969
734C - Антон и зельеварение
In this problem I'll discuss two things — input and binary search.
First, we need to read a huge number of integers, possibly up to 8 * 105 numbers. When you try to read a line with 105 integers in this way:
xs <- (map read . words) `fmap` getLine :: IO [Int64]
It will give you TLE. Believe me, parsing with String and read is really, really slow. Here is my favorite approach:
import Data.Maybe (fromJust)
import qualified Data.ByteString as BS
import qualified Data.ByteString.Char8 as BS8
getInts = (map (fst . fromJust . BS8.readInt) . BS8.words) `fmap` BS.getLine :: IO [Int]
getInt64s = (map (fromIntegral . fst . fromJust . BS8.readInteger) . BS8.words) `fmap` BS.getLine :: IO [Int64]
It performs in reasonable time, but what about space? If you see my submission you will notice that the memory usage is 64 MB. In C++, to hold 8 * 105 integers of 64-bit, you only need (100000 * 8 * 8) bytes = 6.1 MB. I'll discuss it in problem F.
Second, we need to use binary search. But I couldn't find a function like std::upper_bound() of C++ STL in Haskell's base package. I implemented it as follow:
upperBound :: Array Int64 Int64 -> Int64 -> Int64 -> Int64
upperBound ary n x = go 0 n where
go lb ub
| lb >= ub = ub
| ary ! mid <= x = go (mid+1) ub
| ary ! mid > x = go lb mid
where mid = (lb + ub) `div` 2
It assumes a few things. ary has elements in indices from 0 to (n-1). It returns an integer from 0 to n. n means x is larger than any elements in ary. This is not an idiomatic Haskell style. It can be generalized as follows:
upperBound :: Ix i
=> Array i e -- array to binary search
-> (i,i) -- left bound, right bound of search
-> e -- element to find the upper bound
-> i -- desired upper bound
But I'll keep going with the first version, as it works well on this problem...
let ub = upperBound ds k s
let freePotion = cs ! (ub - 1)
let noFirst = if ub > 0 then (max (n - freePotion) 0) * x else n * x
let bestUsingFirst = minimum $ map (make as bs cs ds n k s) [0..m-1]
print $ min noFirst bestUsingFirst
This is the code that finds the answer. Here comes lazy evaluation. ub can be 0 but freePotion doesn't mind it. freePotion is used to evaluate noFirst, only when ub > 0. Hence freePotion = cs ! (-1) never happens.
Last thing, a parade of parameters to make. If I defined make like let make i = ... with other lets, as bs cs ds n k s are not needed:
let ub = upperBound ds k s
let freePotion = cs ! (ub - 1)
let noFirst = if ub > 0 then (max (n - freePotion) 0) * x else n * x
let make i -- define make here
| bs ! i > s = maxBound :: Int64
| otherwise = (max 0 remain) * (as ! i)
where
remain = n - (if ub == 0 then 0 else (cs ! (ub - 1)))
ub = upperBound ds k (s - bs ! i)
let bestUsingFirst = minimum $ map make [0..m-1]
print $ min noFirst bestUsingFirst
It causes parse error, meanwhile in my desktop there's no problem. I use GHC 8.x and Codeforce's GHC version is 7.x. That's the reason I guess.
code: 22285536
734D - Антон и шахматы
Input is not just a list of integers, but a list of (char, int, int). Again, if you try to parse it with String and read:
main = do
...
blacks <- replicateM n $ do
[post, x, y] <- words `fmap` getLine
return (post, read x :: Int, read y :: Int)
...
You will receive TLE. ByteString will save us again.
import Data.Maybe
import qualified Data.ByteString as BS
import qualified Data.ByteString.Char8 as BS8
parseInt = fst . fromJust . BS8.readInt
main = do
...
blacks <- replicateM n $ do
[post, x, y] <- BS8.words `fmap` BS.getLine
return (BS8.unpack post, parseInt x, parseInt y)
...
Remaining parts are done just as the editorial says. But as you can see a lot of memory is used — 167 MB! My C++ code only used 15 MB. It's same situation as problem C. The reasons are list and tuple. in case of tuple, we have to unpack three elements of tuples. My previous post discusses the same problem and as I said I'll return to this in problem F.
code: 22286544
734E - Антон и дерево
Although the input is a tree, I'll consider it as an undirected graph. If it were C++, I would wrote as follow:
vector<int> G[MAX];
for(int i=0; i<n; i++){
int u, v;
cin >> u >> v;
G[u].push_back(v);
G[v].push_back(u);
}
How to do the same thing in Haskell? To model the sample tree in the problem there are several choices.
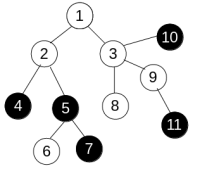
List of List
adj = [[], [2,3], [4,5], [1,8,9], [2], [2,6,7], [5], [5], [3], [3,11], [3], [9]]
i-th element of adj is the list of neighbors of vertex i. It's definitely useless because we need random access on vertices. random access on list, well, good luck.
Adjacency matrix using 2D array
n up to 200000. At least 1525 GB of memory is needed :(
Adjacency list using Data.Map.Strict
import qualified Data.Map.Strict as Map
type Graph = Map.Map Int [Int]
type Edge = (Int,Int)
buildG :: [Edge] -> Graph
buildG es = foldl addEdge Map.empty es
addEdge :: Graph -> Edge -> Graph
addEdge g (u,v) = Map.insertWith (++) u [v] (Map.insertWith (++) v [u] g)
This is a walkable approach, but we can do better regarding that vertices are numbered in compact from 1 to n.
Adjacency list using Data.Array
import Data.Array
import Data.Tuple (swap)
type Graph = Array Int [Int]
buildG :: [Edge] -> Int -> Graph
buildG es n = accumArray (flip (:)) [] (1,n) es
main = do
...
edges <- ...
let edges' = edges ++ (map swap edges)
let g = buildG edges' n
...
Graph representation is fine. To calculate the diameter of it, we need two vertices in longest distance. It's simple:
- Start DFS or BFS on random vertex (say, 1). Find a vertex with maximum level. Let's call it
u. - Start DFS or BFS on vertex
u. Find a vertex with maximum level. Let's call itv. - The diameter is the level of
v.
It's a piece of cake to implement above in C++, but it's not that simple in Haskell.
I seperated the traversal into two steps: generating a list that represents DFS order and creating an array of tuples of (vertex, level). Here is my first try to generate the DFS order list:
preorder :: Graph -> Int -> [(Int,Int)]
preorder g start = dfs start start where
dfs parent v = (v,parent) : concatMap (dfs v) (filter (/= parent) (g ! v))
In this problem we need to compare a vertex's color with it's parent vertex's color, so I zipped each vertex with it's parent.
At first it looked simple, elegant, and efficient... until I got TLE. this version of preorder is incredibly slow as n (number of vertices) goes big. For example,
n = 200000
colors = 1 0 1 0 1 0 1 0 ...
edges = 1 2
2 3
3 4
...
199999 200000
For this simple chain preorder took 50 seconds to terminate. I guess concatMap part is the bottleneck, but can't assure. If someone knows the exact reason, please let me know.
UPD: Thinking ko_osaga's suggestion I expanded the evaluation of dfs. In the case above all of adjacency lists contain just one neighbor vertex. So it is expanded like this:
(1,1) : ((2,1) ++ []) : ((3,2) ++ []) : .... : ((n,n-1) ++ []) : []
It's time complexity is O(n). But concatMap is defined using foldr which lazy evaluate expressions. dfs constructs a very long expression containing up to 200000 calls of foldr and then starts to evaluate the expression. I think building this expression takes most of the execution time.
Next try was generating BFS order. In this time I used Data.Sequence to merge visit orders.
import qualified Data.Sequence as Seq
import Data.Foldable (toList)
preorder :: Graph -> Int -> [(Int,Int)]
preorder g start = toList $ bfs Seq.empty [(start,start)] where
bfs nodes [] = nodes
bfs nodes queue = bfs (nodes Seq.>< Seq.fromList queue) (concatMap nexts queue)
nexts (v,parent) = map (\u -> (u,v)) $ filter (/= parent) (g ! v)
Seq is deque-like data structure and the time complexity of merging two Seq by (><) is O(log(min(n,m))) where n and m are lengths of two sequences. This version of preorder was reasonably fast which made me conclude that concatMap was the problem.
Now we know in which order vertices should be visited. Traverse the graph and calculate each vertex's level based on the level of the parent of the vertex. (caution: We didn't compress the graph, that is we didn't merge adjacent vertices of same color. So if a vertex v and it's parent have same color, v has the same level with its parent.)
code: 22324674
734F - Антон и школа
The size of arrays b and c is up to 200000. If We read b, c and calculate d, a of the editorial as follow:
main = do
n <- getInt
bs <- getInts -- defined as problem C
cs <- getInts
let ds = zipWith (+) bs cs
let as = ... -- get the original array
There will be four [Int], each containing 200000 integers. If a list contains n integers it consumes 5n words. In this case 4000000 words = 4000000 * 64 bytes are needed. Well... it's 244 MB. Moreover we need more arrays than a, b, c, and d.
Clearly the problem is List. Fortunately in this problem we can use unboxed array because all elements of input are required in entire calculation and they are all integers.
At first, reading input as [Int] should be avoided:
import Data.Array.IArray
import Data.Array.Unboxed
getIntArray n = listArray (1,n) `fmap` getInts :: IO (UArray Int Int)
main = do
n <- getInt
bs <- getIntArray n
cs <- getIntArray n
What? It construct an unboxed array but still uses getInts to build it! But this time that [Int] is garbage collected as soon as each integer is filled in the array, so [Int] of length 200000 is never made. This is a funny part of Haskell ;)
There are several lines that contain elems as which is passed to map and forM_ as a parameter. My GHC 8.x is fine with traversing array (as is UArray), but Codeforces' GHC raise a compile error. I guess array is not an instance of Traversable in GHC 7.x. List is surely an instance of Traversable, and elems returns the list representation of elements of an array.
As a result total memory usage is 81 MB which is comparable to my C++ code (54 MB.)
code: 22329902










