Time limit for this test was 1 hour
150 points
200 points
250 points
My solution for 250 points (sorry for bad formatting)
Comments
Feel free to share your ideas/code on how to solve them.
→ Обратите внимание
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3803 |
| 2 | jiangly | 3707 |
| 3 | Benq | 3627 |
| 4 | ecnerwala | 3584 |
| 5 | orzdevinwang | 3573 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | Radewoosh | 3542 |
| 9 | jqdai0815 | 3532 |
| 10 | gyh20 | 3447 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | awoo | 163 |
| 2 | maomao90 | 162 |
| 3 | adamant | 161 |
| 4 | maroonrk | 152 |
| 5 | -is-this-fft- | 151 |
| 6 | nor | 150 |
| 7 | atcoder_official | 147 |
| 7 | SecondThread | 147 |
| 9 | TheScrasse | 146 |
| 10 | Petr | 145 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 04.07.2024 23:59:13 (j2).
Десктопная версия, переключиться на мобильную.
При поддержке
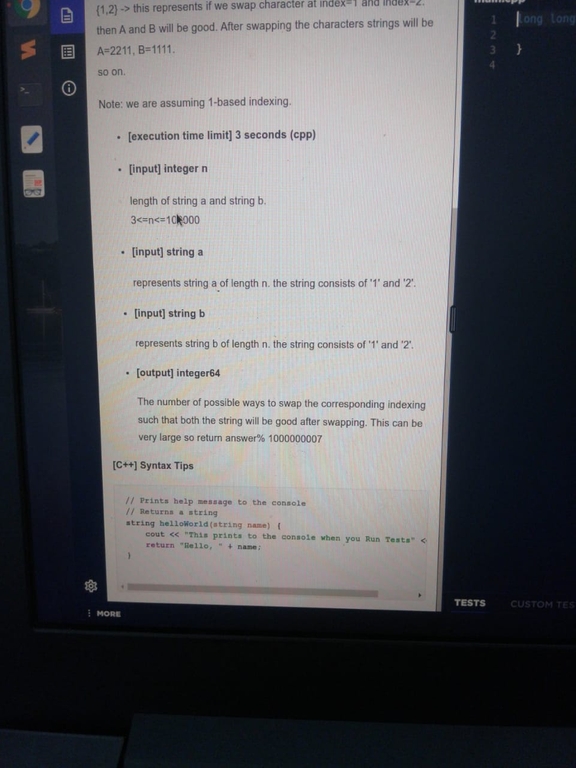
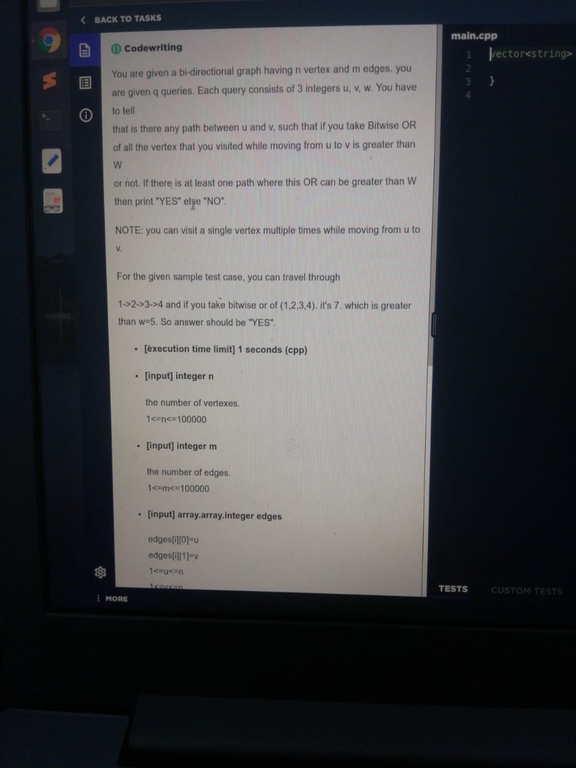
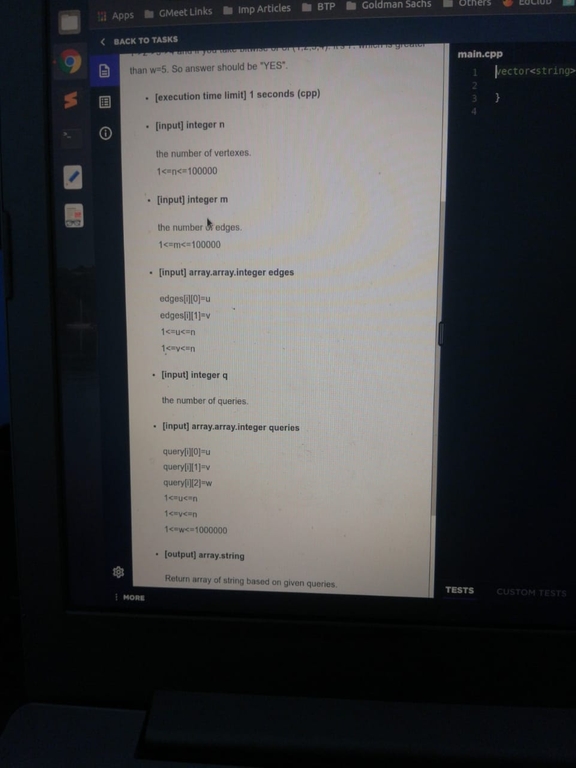
I think the second problem(200 points) can be solved by compressing the graph into a bridge tree and then using binary lifting to obtain the bitwise or of all nodes on the path from the component of u to the component of v.
How to solve the first problem?
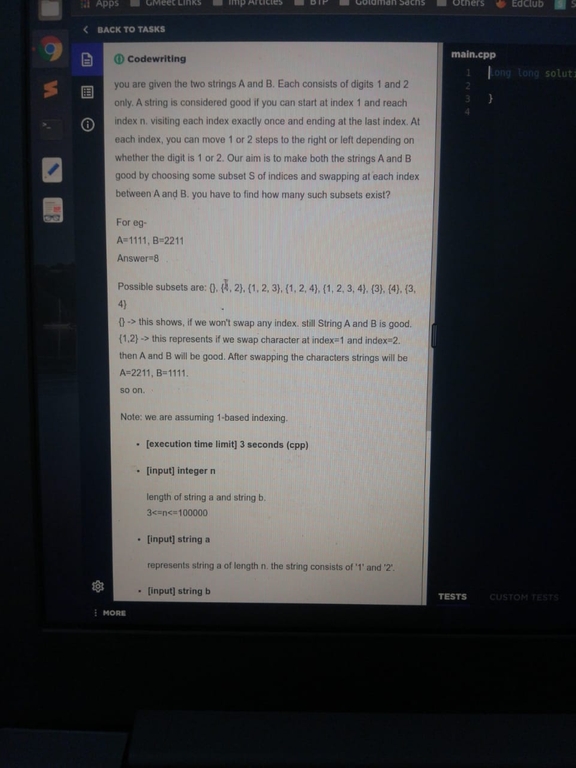
Notice how for every position i in our process we end up either at i , either at i+1 ( this is because the values are <= 2 ).
let dp[i][true/false][true/false] be the number of subsets such that in the process we end up at position i in the first string ( if true ) and at position i+1 ( if false ), similarly for the third state in the second string.
How to transition ?
just take some cases , if we reach position i in the first string and s[i] = 2 then this will go to dp[i+1][false][k].
This way , we have an O(N) solution.
Problem A has been asked in Media.net previously.
Couldn't find a solution earlier too.
Problem A
Round 2 (same Problem)
Second question can be solved with help of DSU. As we can visit any vertex multiple times, so if the OR of whole component will be < w then the answer will be NO. Also problem statement was not correct, it should be greater than or equal to w to pass all the testcases.
The statement is very vague in its definition of what exactly path is, I assumed path to be one where we cannot visit edges twice, Which makes it a way tougher question for a coding test (The solution above using bridge tree seems to be correct).
We can even convert the graph into a weighted one where the cost to go from node a to node b is a bitwise OR b similar for the reverse direction and simply run tweaked Dijkstra to find the maximum distance from every query, but it would get TLE, cuz of O(q*(v+e)*logE). But we can simply take OR of all vertices from 1 to n and address each query in O(1) by checking if it's greater than w or not. There is no use for DSU right, it's greedy.
codebuster_10 , how did you get these 21's in your matrix, for the 250 points question. I am getting the same matrix without the 21's along the diagonal.
21 stands for case when we choose consonants
Ahh I see, I completely forgot about considering consonants.
Was this an on campus test or off campus one?
Off campus
what was your dp state for 250 points problem? codebuster_10
UPD: got it dp[i][j] -> # of ways to get j vowels odd number of times with i as the string length
I think overall every task seems copied or classic. I have seen each one of them before.
task 1 copied from cc , task 3 copied from techgig final round 2019 or 2020 maybe , but doesn't matter due to being so classic , task 2 i have seen before but not sure where. its parade of copied task lol.
task 1] https://www.codechef.com/problems-old/CHEFTWOS
task 2] seems classic
task 3] can be solved with exponential generating functions easily,
it would be coeffiecient of x^N in the below polynomial
$$$ {(\frac{e^{x} - e^{-x}} { 2}})^5 * e^{21x}$$$
multiplied by N!
even though N! would be large but it also would be divided by some K! K would be very large too.