doomsfear's blog

DP or something else

By doomsfear, 11 years ago, In English

I want to get nth digit of the lucky string . Lucky string is made by the concatenation of lucky digits i.e. 4 and 7 in the increasing order . Thus lucky string is 4744477477444.... and so on.

Value of n is of the order 10^15 .

How to solve this type of problem ? Is there any DP solution ?

Example : n=1 ans is 4 . n=10 ans is 4.

  • Vote: I like it
  • -8
  • Vote: I do not like it

»
11 years ago, # |
  Vote: I like it 0 Vote: I do not like it

You don't specify clearly how the lucky string is created. Is it "1x4,1x7,3x4,2x7,5x4,3x7,7x4,4x7,9x4,5x7,..." (2k - 1 consecutive 4-s and k conecutive 7-s)?

If it is (or, more generally, if the numbers of consecutive 4-s and 7-s increase linearly), there's a formula for how many digits will be written before the block of 2k - 1 4-s. It's

using which you can bin-search the largest k such that there are D ≤ N - 1 digits written before that block of 2k - 1 4-s; that means the digit you're looking for is either in the next following block of 2k - 1 4-s (if N - D ≤ 2k - 1) or in the next block of k 7-s (if N-D > k$). From that, you have the answer directly.

Note that there's also an O(1) solution where you solve the inequality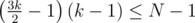 in integer k, but it's unnecessary, since bin-search is really fast.

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    He may also have meant a concatenation of 4, 7, 44, 47, 74, 77, 444, ... but omit 77 by mistake.

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Yeah i meant the concatenation of lucky numbers in the increasing order . Lucky numbers are numbers having only 4 and 7 as their digits . So , after concatenation the lucky string will be like this 4744477477444.... . I want to find the nth character of this string and it would be helpful if i can get a generalized approach .

      → Reply
      • »
        »
        »
        »
        11 years ago, # ^ |
          Vote: I like it +10 Vote: I do not like it

        In short:

        1. Let us divide the string into segments: segment X contains all X-digit numbers. There are 2X numbers of X digits, and their total length is 2X·X. Since the latter value grows exponentially, you can iterate on X until you found the X and the number of the digit in the corresponding segment.

        2. Now, the problem is to find Y-th digit in the string of all X-digit numbers concatenated. When all components have the same length, it is simple. Divide Y by X, convert to binary, make 4s from 0s and 7s from 1s, and take the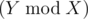 -th digit of the result. You may have to make the numbering 0-based instead of 1-based for convenience.

        → Reply
      • »
        »
        »
        »
        11 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Just in case you were curious, counting the total number of digits Dk of all lucky numbers with less than k digits:

        but also

        Dk = Dk - 1 + (k - 1)·2k - 1

        from which we get

        Dk - 1 = (k - 1)·2k - 1 - 2k + 2

        or equivanently

        Dk = (k - 2)·2k + 2
        → Reply