→ Pay attention
→ Streams
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | jiangly | 3898 |
| 2 | tourist | 3840 |
| 3 | orzdevinwang | 3706 |
| 4 | ksun48 | 3691 |
| 5 | jqdai0815 | 3682 |
| 6 | ecnerwala | 3525 |
| 7 | gamegame | 3477 |
| 8 | Benq | 3468 |
| 9 | Ormlis | 3381 |
| 10 | maroonrk | 3379 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 168 |
| 2 | -is-this-fft- | 165 |
| 3 | Dominater069 | 161 |
| 4 | atcoder_official | 160 |
| 5 | Um_nik | 159 |
| 6 | djm03178 | 157 |
| 7 | adamant | 153 |
| 8 | luogu_official | 151 |
| 9 | awoo | 149 |
| 10 | TheScrasse | 146 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/02/2025 08:04:01 (l2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











I know an O(n * sqrt(n)) approach, but I don't know its proof. I think proving it is difficult, so just take it as magic :)
Let P(n) = number of partitions of n.
Then, P(n) = P(N — 1) + P(N — 2) — P(N — 5) — P(N — 7) + ...
The k-th term of sum in absolute value is P(N — x[k]). The signs of sum's terms alternate from 2 to 2, so they are ++--++--++-- and so on. By x[k] I noted k-th pentagonal number . By formula of pentagonal numbers it's easy to see that when calculating P(n) you add about sqrt(n) numbers (because there are about sqrt(n) pentagonal numbers <= n) so complexity is O(n * sqrt(n)).
Well, proving it is reading the Wikipedia article on pentagonal numbers :D Aside from that, an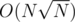 approach should pass comfortably.
approach should pass comfortably.