Given an array of N positive integers a = {a1, a2, a3,......, an},
Find a pair of integers (ai, aj) such that gcd(ai, aj) = 1
Constraints:
- 2 <= N <= 105
- 1 <= ai <= 106
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | jiangly | 3976 |
| 2 | tourist | 3815 |
| 3 | jqdai0815 | 3682 |
| 4 | ksun48 | 3614 |
| 5 | orzdevinwang | 3526 |
| 6 | ecnerwala | 3514 |
| 7 | Benq | 3482 |
| 8 | hos.lyric | 3382 |
| 9 | gamegame | 3374 |
| 10 | heuristica | 3357 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 169 |
| 2 | -is-this-fft- | 162 |
| 3 | Um_nik | 161 |
| 3 | atcoder_official | 161 |
| 5 | djm03178 | 157 |
| 5 | Dominater069 | 157 |
| 7 | adamant | 154 |
| 8 | luogu_official | 152 |
| 9 | awoo | 151 |
| 10 | TheScrasse | 148 |
Given an array of N positive integers a = {a1, a2, a3,......, an},
Find a pair of integers (ai, aj) such that gcd(ai, aj) = 1
Constraints:
| Название |
|---|



correct me if i am wrong but can't this be solved using sieve? you can count number of multiples of k that is presented in your array where 1 < k <= 1e6 then whenever you find that you have number of multiple of k less than n and greater than or equal 1 all you need to is taking any number that is multiple of k with any number that isn't multiple of k time complexity O(klogk)
Okay.This only make sure that those 2 numbers won't have k as a common divisor. But it is possible that they have other divisors common, making gcd > 1. We need to make sure they don't have any divisor common. Say a = {x=2*5, y=3*5}. If you set k=2, then still gcd(x,y) = 5
https://codeforces.net/contest/548/problem/E Here is a similar problem we can use inclusion and exclusion for this one and simple formula Nc2 we can solve this in o(n) * 2^7 7 is the max number of unique primes for any number lessthan 1e6 we can do it using bitmaks 01 bick the prime or leave it or we can use backtracking for the same idea Or we can solve it in o(n) * the number of divisors for each element search about that
what i think here is
we have to make a smallest prime factor for each no and store them now we create some hashset which contains the no of smallest prime factor divisor now we know that the no of pair of frequency of all the smallest individual prime no and we just calculate the all pair using some mathmetical calculations and the ans is [total pair] — [total pair which gcd >1] for example 2 4 6 8 3 9 so the point is
number-> smallest prime factor
2 -> 2
4 -> 2
6 -> 2
8 -> 2
3 -> 3
9 -> 3 so roughly we have 2's -> 4 time and 3-s -> 2 time
sorry i am bit lazy please complete this on your own :)
The number of pairs having gcd = 1 can be found using sieve of eratosthenes. Problem is to find some index i and j for which gcd(ai, aj) = 1
Please refer to this formula.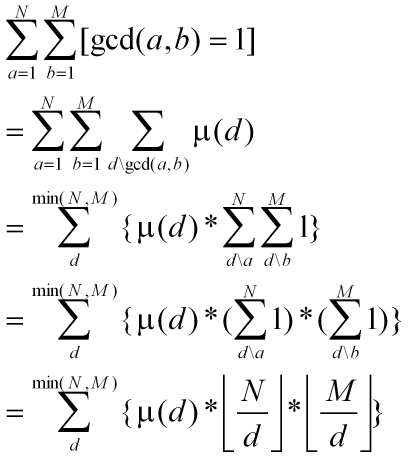
We just change the floor value of N/d to the multiple of d. We apply the sieve of Eratosthenes to find the number of multiple of d. My implementation is below. I hope it will help you.
I assume your code returns the number of such pairs for which gcd = 1, but the problem is to find some index i and j for which gcd(ai, aj) = 1
the result of my code is the pair of (i j),which satisfys that gcd(ai,aj)=1.Please refer to my input section. You can also run this code to verify my words
Your code printing only the "ans" variable which you are printing in line 78
Oh,sorry. I misunderstand your problem statement. It is my fault.
You can run binary search for the first prefix of $$$a$$$ such that the count of pairs with gcd equal to 1 is greater than 0. Let it be $$$i$$$. Then just iterate over all $$$j < i$$$ and check if $$$(j, i)$$$ works.
Thanks!
what is $$$\mu(d)$$$ here?
it means the mobius function.
Check if any of them is 1, if found, then yes
Else, count the multiples of ai in the array, the count should be n if there is no j, such that gcd(ai, aj) = 1
Overall, you can solve this in AlogA, where A is 1e6
I guess this is necessary, but not sufficient. However, the problem requires explicitly the indices i, j for which gcd(ai, aj) = 1
Maybe if you sort it it can work?
Don't think so. If you have an idea please elaborate a little more
I was thinking that if you find some element that isn't a multiple of the smallest value, it may be coprime with the smallest value. Otherwise they all have a common divisor
The smallest value can be composite like this one
a = {2*3, 2*5, 3*5}
Yeah you are right
I think the condition is sufficient, if you have any edge case, let me know. Also, to find the pair of indices, you can just break at the index (let's say i) for which count < n, and then check for every index j, for which gcd(ai, aj) = 1
Hey! Do you have an opportunity to submit a solution for this task? If it's possible for everyone, could you share the link please?
Unfortunately, there is not one
I think that you can just sort your array in increasing order. After that you iterate over all i And you should check every j, such that i — 20 <= j < i. I think that is enough because the product of the smallest 20 primes is bigger than 1e6
Look up Möbius inversion
For each $$$x\le 10^6$$$, count how many multiples of $$$x$$$ there are in the array, and store this value in $$$\textrm{cnt}[x]$$$.
For each element $$$a_i = p_1^{k_1}p_2^{k_2}\cdots p_m^{k_m}$$$ in the array, the number of elements in the array coprime to $$$a_i$$$ can be calculated by the inclusion-exclusion principle which gives the formula
Now for each array element we check if this value is non-zero, and if it is, we break and use another loop to find the corresponding element.
Thanks. One thing I want to ask. How did you convert that inclusion-exclusion equation into something of mobius function?
That's kinda how mobius function is defined actually
According to Wikipedia,
$$$\mu(n)=+1$$$ if $$$n$$$ is a square-free positive integer with an even number of prime factors.
$$$\mu(n)=-1$$$ if $$$n$$$ is a square-free positive integer with an odd number of prime factors.
$$$\mu(n)=0$$$ if $$$n$$$ has a squared prime factor.
(Square-free means the integer isn't divisible by any square of a prime.)
So basically summing over the divisors $$$d$$$ of a number $$$n=p_1^{k_1}p_2^{k_2}\cdots p_m^{k_m}$$$ looks like
$$$\sum_{d\vert n}\mu(d)f(d) $$$
$$$= 1 - (f(p_1) + \cdots + f(p_m)) + (f(p_1p_2) + \cdots + f(p_{m-1}p_m)) - \cdots + (-1)^mf(p_1p_2\cdots p_m)$$$
Because all the terms where a prime has a power greater than one will have a coefficient of $$$\mu(d)=0$$$
I highly recommend reading these CP tutorials as well: zhtluo.com
I think dropping prime powers gives a better complexity here
Lol i literally just came here to post about it when i realized and then I saw your comment
Iterate from 0..i until we get gcd(a0,a1,...,ai)=1, then can we say that there is an element at j from 0..i — 1 that gcd(aj,ai) == 1?
counterexample : $$$a = [6, 15, 10]$$$
Thanks:)
https://ideone.com/cOvEqC here is my solution, its complexity is O(n * 2^p) where p is at most 8. there is a corner case that can be handled easily which is when the gcd of all the array is greater than 1
The loop calculating the array $$$\textrm{cnt}$$$ is $$$O(n\log{n})$$$
yes I forget it
Thanks!
Initial idea, might be wrong. Lets count gcd of our array from the start. At some index, lets call it $$$i$$$, it will turn to 1, that means that gcd of $$$a[i]$$$ and some element in $$$a[:i]$$$ equals one. Factorize $$$a[i]$$$ and for every its factor mark elements on our prefix that are divisible by it. In the end, we will have some unmarked indexes — take any of them.
counterexample : $$$a=[6,15,10]$$$
find index for which prefix gcd equals to 1 and that will absolutely 1 of the number. then iterate over all the array and find another number which is coprime to the number at that index.
Your idea is not correct. a = {2*3, 2*5, 3*5} is a counter example
in this case solution doesn't exist.
Which proves your algorithm doesn't work...
we will not get a 2 nd element in this case.
If we only want to find one such pair of ai, aj than we can divide it into two part :
base case if 1 is in the array just print it with any number
Part — 1 : Lets focus on finding one of the elements in the array a, such that the no. of elements that have gcd != 1 with it are < n — 1 , we can find it using the inclusion exclusion,
Part — 2 : we alreadty know one ai that gives me the solution than I can just iterate over entire array and find aj such that gcd(ai, aj) = 1