Idea: BledDest
Tutorial
Tutorial is loading...
Solution (BledDest)
def check(x):
s = str(x)
cnt = 0
for c in s:
if c != '0':
cnt += 1
return cnt == 1
a = []
for i in range(1, 1000000):
if check(i):
a.append(i)
t = int(input())
for i in range(t):
n = int(input())
ans = 0
for x in a:
if x <= n:
ans += 1
print(ans)
Idea: BledDest
Tutorial
Tutorial is loading...
Solution (awoo)
for _ in range(int(input())):
n = int(input())
s = input()
cur = {}
for i in range(n - 1):
t = s[i:i+2]
if t in cur:
if cur[t] < i - 1:
print("YES")
break
else:
cur[t] = i
else:
print("NO")
Idea: BledDest
Tutorial
Tutorial is loading...
Solution (awoo)
for _ in range(int(input())):
n = int(input())
s = [input() for i in range(2)]
pos = -1
for i in range(n):
if s[0][i] != s[1][i]:
pos = i
if pos == -1:
print("YES")
continue
ok = True
cur = 0 if s[0][pos] == 'B' else 1
for i in range(pos + 1, n):
if s[cur][i] == 'W':
ok = False
if s[cur ^ 1][i] == 'B':
cur ^= 1
cur = 0 if s[0][pos] == 'B' else 1
for i in range(pos - 1, -1, -1):
if s[cur][i] == 'W':
ok = False
if s[cur ^ 1][i] == 'B':
cur ^= 1
print("YES" if ok else "NO")
Idea: BledDest
Tutorial
Tutorial is loading...
Solution (adedalic)
#include<bits/stdc++.h>
using namespace std;
#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
#define sz(a) int((a).size())
typedef long long li;
const int INF = int(1e9);
const int N = int(1e7) + 5;
int mind[N];
void precalc() {
fore (i, 0, N)
mind[i] = i;
for (int p = 2; p < N; p++) {
if (mind[p] != p)
continue;
for (int d = 2 * p; d < N; d += p)
mind[d] = min(mind[d], p);
}
}
int x, y;
inline bool read() {
if(!(cin >> x >> y))
return false;
return true;
}
vector<int> getPrimes(int v) {
vector<int> ps;
while (v > 1) {
if (ps.empty() || ps.back() != mind[v])
ps.push_back(mind[v]);
v /= mind[v];
}
return ps;
}
inline void solve() {
int d = y - x;
if (d == 1) {
cout << -1 << '\n';
return;
}
int r = INF;
for (int p : getPrimes(d))
r = min(r, ((x + p - 1) / p) * p);
cout << r - x << '\n';
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
int tt = clock();
#endif
ios_base::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cout << fixed << setprecision(15);
precalc();
int t; cin >> t;
while (t--) {
read();
solve();
#ifdef _DEBUG
cerr << "TIME = " << clock() - tt << endl;
tt = clock();
#endif
}
return 0;
}
Idea: BledDest
Tutorial
Tutorial is loading...
Solution (BledDest)
#include<bits/stdc++.h>
using namespace std;
const int N = 300043;
int n;
int v[N];
map<vector<int>, long long> dp[N];
pair<int, vector<int>> go(vector<int> a, int x)
{
if(x == 0)
return {1, a};
else
{
bool f = false;
for(int i = 0; i < a.size() && !f; i++)
if((a[i] & x) > 0)
{
f = true;
a[i] = x;
}
int c = 0;
if(!f)
{
c = 1;
a.push_back(x);
}
return {c, a};
}
}
long long calc(int i, vector<int> a)
{
if(i == n) return 0ll;
if(dp[i].count(a)) return dp[i][a];
auto p = go(a, v[i]);
return (dp[i][a] = p.first * 1ll * (n - i) + calc(i + 1, p.second));
}
int main()
{
scanf("%d", &n);
for(int i = 0; i < n; i++) scanf("%d", &v[i]);
long long ans = 0;
for(int i = 0; i < n; i++)
ans += calc(i, vector<int>(0));
printf("%lld\n", ans);
}
Idea: BledDest
Tutorial
Tutorial is loading...
Solution (BledDest)
#include <bits/stdc++.h>
using namespace std;
const int N = 243;
struct edge
{
int y, c, w, f;
edge() {};
edge(int y, int c, int w, int f) : y(y), c(c), w(w), f(f) {};
};
vector<edge> e;
vector<int> g[N];
int rem(int x)
{
return e[x].c - e[x].f;
}
void add_edge(int x, int y, int c, int w)
{
g[x].push_back(e.size());
e.push_back(edge(y, c, w, 0));
g[y].push_back(e.size());
e.push_back(edge(x, 0, -w, 0));
}
int n, m, s, t, v;
pair<int, long long> MCMF()
{
int flow = 0;
long long cost = 0;
while(true)
{
vector<long long> d(v, (long long)(1e18));
vector<int> p(v, -1);
vector<int> pe(v, -1);
queue<int> q;
vector<bool> inq(v);
q.push(s);
inq[s] = true;
d[s] = 0;
while(!q.empty())
{
int k = q.front();
q.pop();
inq[k] = false;
for(auto ei : g[k])
{
if(rem(ei) == 0) continue;
int to = e[ei].y;
int w = e[ei].w;
if(d[to] > d[k] + w)
{
d[to] = d[k] + w;
p[to] = k;
pe[to] = ei;
if(!inq[to])
{
inq[to] = true;
q.push(to);
}
}
}
}
if(p[t] == -1 || d[t] >= 0) break;
flow++;
cost += d[t];
int cur = t;
while(cur != s)
{
e[pe[cur]].f++;
e[pe[cur] ^ 1].f--;
cur = p[cur];
}
}
return make_pair(flow, cost);
}
void no_answer()
{
cout << "Impossible" << endl;
exit(0);
}
int main()
{
cin >> n >> m;
vector<int> excess_flow(n, 0);
vector<int> orc(m);
for(int i = 0; i < m; i++)
{
int x, y, c, w;
cin >> x >> y >> c >> w;
orc[i] = c;
--x;
--y;
add_edge(x, y, c / 2, w);
if(c % 2 == 1)
{
excess_flow[x]--;
excess_flow[y]++;
}
}
s = n;
t = n + 1;
v = n + 2;
int total_excess = 0;
if(excess_flow[0] % 2 == -1)
{
excess_flow[0]--;
excess_flow[n - 1]++;
}
for(int i = 0; i < n; i++)
{
if(excess_flow[i] % 2 != 0)
no_answer();
int val = abs(excess_flow[i]) / 2;
if(excess_flow[i] > 0)
{
total_excess += val;
add_edge(s, i, val, -int(1e9));
}
if(excess_flow[i] < 0)
{
add_edge(i, t, val, -int(1e9));
}
}
add_edge(s, 0, 100000, 0);
add_edge(n - 1, t, 100000, 0);
auto ans = MCMF();
bool good_answer = true;
for(int x = 0; x < e.size(); x++)
if(e[x].w == -int(1e9) && rem(x) != 0)
good_answer = false;
if(!good_answer)
no_answer();
cout << "Possible" << endl;
for(int i = 0; i < 2 * m; i += 2)
{
if(i) cout << " ";
cout << e[i].f * 2 + orc[i / 2] % 2;
}
cout << endl;
}










ratttttttttttttttttttttttttttttttttttttttttttttttttttttting plz
LOL, why so many downvotes.
I had a dream, not being newbie when attending Turkish Junior National Olympics in Informatics but because of the slowest rating update ever,i can't
When will the ratings update? :(
It is the first time that I will have a oringe name. I really want it could update rating as quickly as possible.plz
i feel for you :(
It's the same for me...plz
me too, it so slow
me too too
I didn't read B properly and thought that $$$n$$$ could take on values other than the length of the input. I thought I needed to implement a complicated LCP+Suffix Array method than ran in $$$O(n*log(n)^2)$$$ to greedily compute the minimum number of operations needed to produce the resulting string, which I wasn't able to do during the contest.
Here's my solution which actually computes the minimum number of operations: 185016918
Didn't it occur to you that you were solving a Div2B and not a Div1B? xD
Ayoooo, Chill... Nice Work man tho :"D
Us moment
In A why 184918763 got TLE?
That's why you are grey.
now is your comment:)
Because you are iterating from 1 to n in each case. So the time complexity would be O(t*n) which would give TLE. You have already calculated if each i is extremely round or not. Just construct a prefix sum array which would tell how many extremely round numbers are less than i. Then you can answer each case in O(1).
Your algorothm takes n (n = the given integer) iterations of the loop for each test case. At worst, your algorithm will have to do $$$999 \ 999$$$ iterations of the loop for each test case. A test set can contain up to $$$10^4 = 10 \ 000$$$ test cases. Your algorithm might need to do $$$10 \ 000 \cdot 999 \ 999 = 9 \ 999 \ 990 \ 000 \approx 10 \ 000 \ 000 \ 000 = 10^{10}$$$ iterations of your loop. C++ can do around $$$10^8$$$ operations on average in one second. Each iteration of your loop contains 4 fast operations:
i<=n,f[i]==1,ans++andi++. Even though these are simple and fast operations, c++ can't execute that many of them in under 3 seconds.For D, we can consider only prime divisors of $$$y-x$$$ because to minimize the answer, if it's possible to get $$$\gcd(x,y) \neq 1$$$ for a certain composite $$$d$$$ s.t. $$$d|(y-x)$$$, it's definitely possible for some prime $$$p < d$$$ and we can reach multiples of $$$p$$$ at least as soon as we reach a multiple of $$$d$$$.
its all code, man.
state transition graph for 1766E([i] represent for a sequence end with i)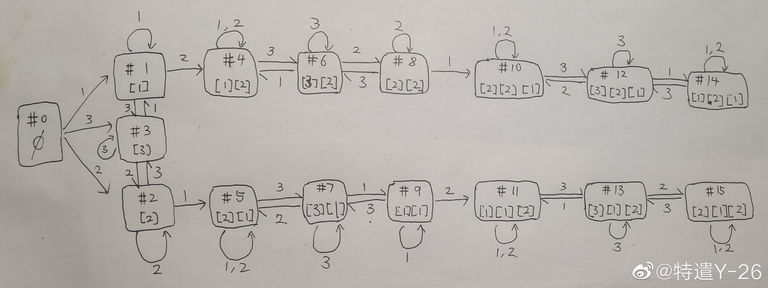
This state transition is sufficient enough to arrive at the intended solution.
Nice round. I think D and E are the best problems I've ever seen.
Video Editorial of Problem C : Hamiltonian Wall Link : https://youtu.be/p4-bUeGfs48
Detailed Solution of Problem D
E is simply brilliant.
The complexity given for B is wrong. It is O(1). There are 26^2 possible unique 2-letter strings. Any string longer than 26^2+1 will have at least one repetition due to the Pigeonhole Principle.
You have to read the string, so it is $$$O(n)$$$. And even if you read it character by character, in order to go to the next test case, you still have to read the whole string.
I still don't understand why we need all the prime divisors of each number in C. Don't we only need the smallest prime divisor to know the earliest point when the chain will stop?
Yeah correct, knowing the smallest is sufficient
No, take the example (4,19), y-x = 15 and the smallest prime factor is 3, however the smallest k that ensures gcd(4+k,19+k) = 3 is k = 2, but with a prime factor of 5, we find the smallest k ensuring gcd(4+k,19+k) = 5 is k = 1. That's why we run over all prime factors and take the minimum k for each.
actually knowing the smallest is suffice because you can iterate x /= least[x] then update the answer, which is a bit faster. My solution during contest: 184938325
Yeah I solved it that way too but I took the OP's question as "why can't you just use the smallest prime alone"
if anyone wants the O(1) solution for A, here it is :)
184929564
What will be the expected rating of the first 3 questions?
when will the rating be updated???
Perhaps the program of calculating rating change has crashed and CF stuffs are calculating manually
what, manually???
I cannot come up with any other idea why rating has not been updated yet now
manually? are you sure there are that many of them during the war?
What does war have to do with this
Why this submission passed problem 2? Surely it's complexity is O(n^2) Your text to link here...
There are only 26^2 = 676 patterns of two successive characters.
It means that this loop will end within at most approx.700*|s| times, and is enough fast to pass.
This is called Pigeonhole principle.
I think any string longer than 704 will always be YES, and I guess the string below might be the longest one that can be NO.
The contest which made me master! 139 is a happy number.
It made me blue! (perhaps back to cyan tommorrow)
Problem- E:- Can anyone tell, which case they where missing while they where getting WA at test case 16.
expected: '1476747', found: '996573'
How to correct it.
Thanks in advance :)
The B solution is wrong: Try this testcase: - t=1 - string='abcdabef' - n=6, - the answer is yes according to solution but it's wrong becuase: - 4 operations for 'abcd', - then 5th operation for copying and appending 'ab' string, - then 6th and 7th operation for 'ef', - so number of operations exceed n.
n must be equal to length of string
Is the concept "smallest prime factor" (
minD) a well-known thing?the pair contribution dp thing is something i've really only seen in digit dp problems, interesting to see it works with subarrays as well :)
https://codeforces.net/contest/1766/submission/262903359
dfs solution for task C