Hello Codeforces!
Today I'll be writing about what I have learnt about combinatorics, which played, and, in my opinion, will still be playing a important role in both Codeforces and CP (short for competitive programming).
However, combinatorics is such a great subject that made that impossible for me to write it all in one blog. So, this is just the very first blog, which is for beginners. If you are interested, please, pay attention to this account and I'll give posts as series for a long term.
If you have found some mistakes in the text, or if you have some questions about the topic, please, leave a comment, and I'll check it weekly and reply. Also, if you find some grammar mistakes, a kind comment will be also welcomed.
Thanks
- HappyIvan, mikcf, rtckyw_ for pointing out some problems in the text.
- guns_baby_jesus, hydra_cody for providing possible topics.
Content
- addition / multiplication principle
- factorial, permutation and combination
- special binomial theorem
- principle of inclusion-exclusion
- pigeonhole principle
- homework
Part 0 — Pre-knowledge
In order not to make this blog too long (it's already very long now xD), I won't explain these things anymore. You can find them on wikis or google them.
- Set theory.
- CP basics.
- Reading simple C++ code.
Part 1 — addition / multiplication principle
What is addition principle?
it is the intuitive idea that if we have $$$A$$$ number of ways of doing something and $$$B$$$ number of ways of doing another thing and we cannot do both at the same time, then there are $$$A + B$$$ ways to choose one of the actions.
Now generally speaking, if we have $$$n$$$ things to do, and we can only do strictly one thing. For the $$$i$$$-th thing, you have $$$a_i$$$ ways to do it. Then there are $$$(a_1+a_2+a_3+\dots a_n)$$$ (or in the lingo, $$$\displaystyle\sum^{n}_{i=1}a_i$$$) ways to choose one of the actions.
What is multiplication principle?
Stated simply, it is the intuitive idea that if there are $$$a$$$ ways of doing something and $$$b$$$ ways of doing another thing, then there are $$$a·b$$$ ways of performing both actions. It means that you have to do the first thing first then the second thing second.
Now generally speaking, if we have $$$n$$$ things to do. For the $$$i$$$-th thing, you have $$$a_i$$$ ways to do it. Then there are $$$a_1\cdot a_2\cdot a_3\dots a_n$$$ ($$$\displaystyle\prod^{n}_{i=1}a_i$$$) ways of performing both actions. It means that the $$$i$$$-th thing comes the $$$i$$$-th and you can only do it strictly once, in a fixed order.
Here is a problem for you to solve:
Mike has $$$a$$$ hats, $$$b$$$ coats, $$$c$$$ pairs of trousers and $$$d$$$ pairs of shoes to choose from. He can choose strictly one coat, one pair of trousers and one pair of shoes. Since it's not very cold so Mike can choose whether he'll wear a hat. But still he can only wear no or $$$1$$$ hat(s). Please count the number of the ways for Mike to choose one of the valid dressing ways.
Here comes the solution:
Part 2 — factorial, permutation and combination
What is factorial?
We define $$$n!=1\times 2\times3\times \dots n$$$. For example: $$$3!=3\times 2\times 1=6$$$.
Respectively, we define $$$0!=1$$$.
You may wonder why we define this, maybe one of the reasons is that, when we define $$$0!=1$$$, then we can define $$$n!$$$ in a recursive way: $$$n!=(n-1)!\times n\ (n\in \mathbb N^+)$$$
Here a question comes: Is this related to what we talk about today? Let's see the problem below:
Count the different versions of an array $$$a_1,a_2,\dots,a_n$$$ which satisfies: — $$$1\leq a_i\leq n$$$. — Every number in the array occurs only one time.
This is also called a permutation of $$$[1,2,3,\dots, n]$$$ or a permutation with its length $$$n$$$. For example $$$[1,3,2,5,4]$$$, $$$[1]$$$ and $$$[3,2,1]$$$ are permutations, while $$$[1,1,1]$$$, $$$[10,13,11,12]$$$ and $$$[1,2,4,5,6]$$$ are not.
Given $$$n$$$, give the answer.
Here comes the solution:
But if we only need to decide an array $$$a_1,a_2,\dots, a_k$$$, which still fits $$$1\leq a_i\leq n$$$ and every number in the array occurs only one time. This is called permutation. The answer is $$$n\times (n-1)\times \dots, (n-k+1)=\frac{n!}{(n-k)!}$$$, which is similar to the previous task, but here we note the answer $$$\frac{n!}{(n-k)!}=P_{n}^{k}$$$ or $$$A_{n}^{k}$$$. Specially, we call the $$$n=k$$$ situation
A new question comes after the last problem: what if the order of the array we construct is no longer important, the array $$$a$$$ and all the permutations of the array $$$a$$$ are all considered the same, how many different arrays are there now?
In the set theory, we can write it out more formally: How many sets $$$s$$$ which fits $$$s\in S$$$, or to say $$$s$$$ is a subset of $$$S$$$, are there when $$$|s|=k,|S|=n$$$?
For each array we count in the last problem, it has $$$k!$$$ same arrays (including itself), so, we have to divide the previous answer by $$$k!$$$. (If you cannot understand here, $$$S=[1,1,2,2,3,3]$$$, isn't the count of different numbers $$$\frac{6}{2}=3$$$? Here it's the same.) So the answer is $$$\frac{n!}{(n-k)!k!}$$$, we note the answer $$$\frac{n!}{(n-k)!k!}=\binom{n}{k}=C_n^k$$$. (But on wikipedia I found it $$$C_k^n$$$, there are many versions of the expression.)
This is called combination.
Here are some interesting features of $$$C_n^k$$$:
1
Actually $$$\binom{n}{k}$$$ doesn't refer to the combination numbers. They refer to the coefficient of the polynomial $$$f(x)=(x+1)^n=\binom{n}{n}x^n+\binom{n}{n-1}x^{n-1}+\binom{n}{n-2}x^{n-2}+\dots+\binom{n}{1}x+\binom{n}{0}$$$. Now we find that when $$$f(x)=(x+1)(x+1)(x+1)\dots(x+1)$$$, if you choose $$$k$$$ $$$x$$$-s from $$$n$$$ $$$x$$$-s, there will be $$$C_n^k$$$ different $$$x^k$$$-s to combine, then the coefficient of $$$x^k$$$ is $$$C_n^k=\binom{n}{k}$$$. Since their value are totally the same, we note $$$\binom{n}{k}$$$ as combination too.
2
$$$\binom{n}{k}=\binom{n-1}{k-1}+\binom{n-1}{k}$$$.
According to this, we can get the value of $$$\binom{n}{m}\bmod k$$$ in $$$\mathcal O(1)$$$ time and $$$\mathcal O(n^2)$$$ initation work:
int lim = 2000;
for(int i = 0; i <= lim; i++) c[i][0] = c[i][i] = 1;
for(int i = 0; i <= lim; i++) {
for(int j = 1; j < i; j++) {
c[i][j] = c[i - 1][j - 1] + c[i - 1][j];
c[i][j] %= k; // We will mention this later.
}
for(int j = i + 1; j <= lim; j++) {
c[i][j] = -1;
}
}
By the way, $$$\binom{n}{m}$$$ is a large number, so we usually get it modulus a number (usually a large prime, the reason will be discussed in the next post in the series).
Part 3 — special binomial theorem
Here we give the equation of special binomial theorem out:
Here $$$\sum\limits_{i=0}^{n}\binom{n}{i}=2^n$$$ denotes to $$$\binom{n}{0}+\binom{n}{1}+\dots+\binom{n}{n-1}+\binom{n}{n}$$$.
Proof:
What about this problem:
How many subsets (empty allowed) of $$$S$$$ are there when $$$|S| = n$$$?
Solution 1: For the subset $$$s$$$, you can choose whether you choose the $$$i$$$-th element in $$$S$$$ or not. Here it fits the multiplication principle, the answer is $$$2\times 2\times \dots\times 2=2^n$$$.
Solution 2: For $$$|s|=0,1,2,\dots,n$$$, the solution is $$$\binom{|s|}{n}$$$. According to the addition principle, the solution is $$$\binom{n}{0}+\binom{n}{1}+\dots+\binom{n}{n-1}+\binom{n}{n}=\sum\limits_{i=0}^{n}\binom{n}{i}$$$
Since the $$$2$$$ solutions points to the same answer, so we get the proof.
An easy trick:
If you want to enumerate all the subsets of $$$S=\lbrace S_1,S_2,\dots,S_n\rbrace$$$ when $$$|S|=n$$$, we can give out a binary string $$$s$$$ of size $$$n$$$ to represent a subset.
- $$$s_i=\texttt 1$$$, when $$$S_i\in s$$$, which denotes that you chose the $$$i$$$-th element.
- $$$s_i=\texttt 0$$$, when $$$S_i\not\in s$$$, which denotes that you didn't choose the $$$i$$$-th element.
But a binary string can be seen as an integer in binary system which $$$\in [0,2^n)$$$. So you can just enumerate the integer. Isn't it faster and easier to implement. than DFS?
Part 4 — principle of inclusion-exclusion
$$$10$$$ students like maths, $$$11$$$ students like dp, $$$12$$$ students like graphs. Students each like at least one thing of these three things. How many students are there in the class? Is it $$$10+11+12=33$$$? No. Because one can like both maths and dp. Or even one can like all the three subjects.
Here we note student that like maths, dp and graphs as $$$A,B,C$$$ respectively. So there are $$$|A\cup B\cup C|$$$ students in class. Moreover:
- $$$|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|B\cap C|-|C\cap A|+|A\cap B\cap C|$$$
View this image for understanding.
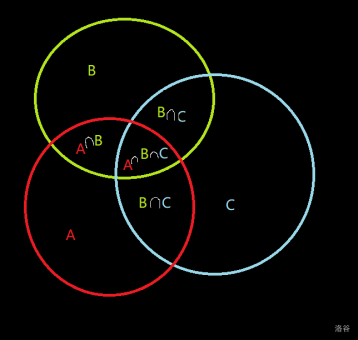
If we promote $$$3$$$ to $$$n$$$, here comes the principle of inclusion-exclusion formula.
There are no tasks temporarily, I'm very sorry. Tasks will be given out after the next post, because without the implementation, it's hard to write, and complain the time complexity out.
In the homework I'll leave some problems instead of here.
Part 5 — pigeonhole principle
It is always used to prove existential problems or something in the worst condition.
Easy condition
There are $$$n+1$$$ pigeons and $$$n$$$ pigeonholes. Prove: There is at least one pigeonhole which as more than one pigeon in it.
More commonly
For $$$m$$$ pigeons in $$$n$$$ pigeonholes, there is at least one pigeonhole with no least than $$$\left\lceil\frac{m}{n}\right\rceil$$$ pigeons.
Proof: for homework, it's pretty easy.
Part 6 — homework
Task A (Maths)
There are $$$k$$$ sets $$$S_1,S_2\dots,S_k$$$, which fits:
- $$$\displaystyle\bigcup_{i=1}^{k} S_i = \lbrace 1,2,3,\dots,n\rbrace$$$
Give out the number of different conditions of $$$S_1,S_2,S_3,\dots, S_n$$$.
Sample: $$$n=2, k=2, ans=9$$$.
Task B (Maths)
I'm standing on the point $$$(0,0)$$$ and I want to walk to the point $$$(n,m)$$$. For each walk, suppose I'm at $$$(i,j)$$$, I can go to $$$(i+1,j)$$$ or $$$(i,j+1)$$$. How many different routes are there for me to finish the walk?
Sample: $$$n=2, m=2, ans=6$$$.
Task C (Maths)
We define $$$S(a,b,c,d)=(a-b)(a-c)(a-d)(b-c)(b-d)(c-d)$$$.
Calculate the value of
Task D (Implementation)
Garlic is a clever girl, she wonders when given $$$n,m,k$$$, How many pairs $$$i,j$$$ fits $$$k|\binom{i}{j}$$$ for all $$$0\leq i\leq n,0\leq j\leq \min \left ( i, m \right )$$$.
There are $$$q$$$ queries of $$$n,m$$$, while the $$$k$$$ is constant.
Input
The first line two integers, $$$q,k$$$.
The following $$$q$$$ lines, for each line, two numbers $$$n,m$$$.
Output
$$$q$$$ lines. For each line, one number represents the answer.
Input Sample
2 5
4 5
6 7
Output Sample
0
7
Data range
$$$1\leq n,m\leq 5000, 1\leq k\leq 50, 1\leq q\leq 10^6$$$
At last
If you're unsure of the solution to the homework:
This blog talks about something easy, maybe it's only a test for the series. Harder things will be mentioned later, such as initation of combinations in $$$\mathcal O(n)$$$ time, Lucas theory and so on.
It really takes time, please, give your valuable comments and advise!
Thanks for reading! This series will be written on.



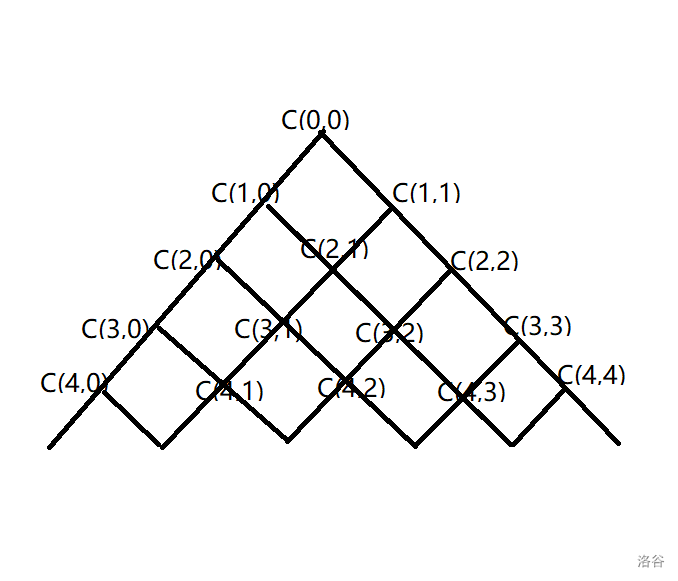
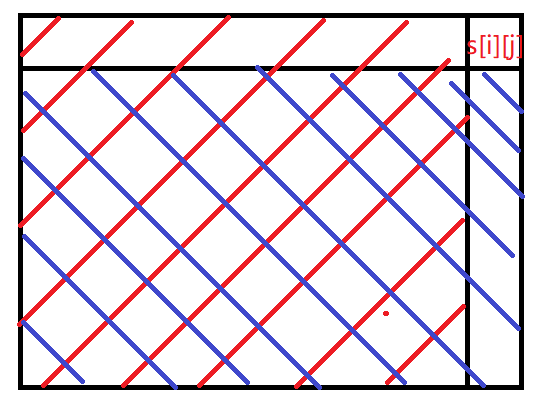








The tutorial of the homework will be given later.
Can you do bitmasks
OK, noted your desire.
+1 probability
Hey, I think that there is a slight mistake in section "Combination", there shouldn't be "6" in f(X) = ... expression (Another tiny mistake is in inclusion-exclusion principle, there shouldn't be "-" in BuC set. Pointing out those cosmetic errors, because blog is quite nice and deserves top quality
Updated, thank you for pointing out this!
Thank you so much for the blog. Much appreciated.
It will be great if you could attach the problem set from codeforces related to combinatorics (basic) level.
After discussing the implementation, I'll do this.
Do you have links to problems?
Can You suggest some good problems to practice ?