PraveenDhinwa's blog

Another Interesting Problem
By PraveenDhinwa, 11 years ago, In English

You are given a string s of size n, consisting of characters A and B only. You have to find minimum sum of size of the two disjoint segments such that number of A's in them are >= z.

Input: string s, n, z are given in the input. Output: minimum sum of size of two disjoint segments with given property

Currently I have a solution of complexity 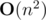, Can anybody give a better solution than this?

Or can somebody prove that it is somehow related to 3 SUM problem?

  • Vote: I like it
  • +6
  • Vote: I do not like it

»
11 years ago, # |
  Vote: I like it +1 Vote: I do not like it

I could only think of an O(n*x) solution

Here is how it goes

find the furthest two adjacent occurrences of letter 'A' (S[i]='A' and S[j]='A' and j>i and S[i+1...j-1] doesn't contain any 'A's and (j-i) is as large as possible)

Now split the string into two strings Sleft (S[1..i]) and Sright (S[j...n])

Now i am sure one of the segments lies completely in Sright and the other lies completely in Sleft

Now for the left segment(substring from Sleft), it can contain any number of 'A's in range(1,max_no_of_As_in_**Sleft**).

Iterate over each of these numbers(let's mark the chosen number as y) and find the length of the shortest substring containing y 'A's ... (Take care u have to iterate from 1 to at most x-1)

Correspondingly find the shortest substring in Sright that contains x-y 'A's

The process of finding the shortest substring containing y 'A's can be done in O(length of the string)

Total complexity O(n*x)

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Hi, I am really sorry for not being able to explain very clearly, please see the latest version, I hope that it is more clear than that.

    Your solution seems like correct to me, I also had similar O(n^2) solution for the problem.

    → Reply