Aveiro_quanyue's blog

Would you please help me with a Nowcoder problem?
By Aveiro_quanyue, history, 19 months ago, In English

Part 1: Problem Statement

Link

A tree $$$T=(V, E)$$$ has $$$n$$$ vertices and $$$n-1$$$ edges, the weight of each vertex $$$i$$$ is $$$a_i$$$.

For each edge $$$e$$$, you can determine its direction, i.e., for two vertices $$$u, v$$$, there are two states: $$$u \rightarrow v$$$ and $$$v \rightarrow u$$$. There are $$$2^{n-1}$$$ states in total.

For each state $$$S$$$, we define $$$f(S)$$$ as

$$$f(S) := \sum\limits_{(u, v) \in V \times V, v\,\text{is reachable from}\,u} |a_u - a_v|$$$.

Compute the sum of $$$f(S)$$$ over all $$$2^{n-1}$$$ states $$$S$$$, modulo $$$998244353$$$.

Example:

Suppose $$$n=3$$$, and two edges connect $$$(1, 2), (2, 3)$$$, respectively. $$$a_1 = 3, a_2 = 1, a_3 = 2$$$, the answer is $$$14$$$.

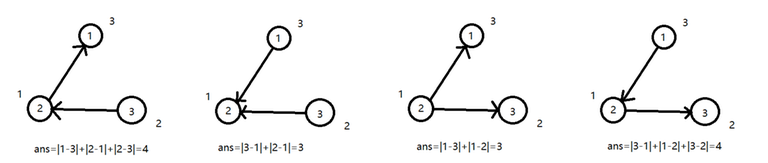
Constraints: $$$2 \leq n \leq 2 \cdot 10^5$$$, $$$1 \leq a_i \leq 10^9$$$.

Part 2: My idea

My only attempt is using the counting twice trick:

$$$ans = 2\sum\limits_{(u, v) \in V \times V, u < v}|a_u - a_v|2^{n-1-d(u, v)} = \sum\limits_{(u, v) \in V \times V, u < v}|a_u - a_v|2^{n-d(u, v)}$$$, but I don't know how to solve it in $$$O(n)$$$ or $$$O(nlogn)$$$.

Maybe we could use $$$d(u, v) = d(u) + d(v) - 2d(lca(u, v))$$$?

  • Vote: I like it
  • +12
  • Vote: I do not like it

»
19 months ago, # |
← Rev. 10   Vote: I like it -35 Vote: I do not like it

I think you can use Centroid Decomposition + Heuristic Merge to solve it.

Spoiler
→ Reply
  • »
    »
    19 months ago, # ^ |
      Vote: I like it +6 Vote: I do not like it

    I upvoted. Would you please elaborate on this please?

    → Reply
    • »
      »
      »
      19 months ago, # ^ |
      ← Rev. 5   Vote: I like it -23 Vote: I do not like it

      Start with Centroid Decomposition (you can think of it as cdq on tree).

      Subsequently, at Centroid Decomposition, the points of the two subtrees are sorted by ai and multiplied by 2^(size of tree-dep of node) to make a prefix sum respectively, so that |ax-ay| becomes ∑ two ax-ay. I'm not sure how to analyze the complexity, maybe nlog^2n .

      → Reply