kllp's blog

The great ternary search hoax
By kllp, 11 years ago, In English

Today I was having troubles remembering how to code ternary search for integers. Through the ages, people have been taught to divide the interval into three equal length parts. Fortunately Sisu told me that I should not... I believe this is a new thing for some people.

while(lo < hi) {
    int mid = (lo + hi) >> 1;
    if(f(mid) > f(mid+1)) {
        hi = mid;
    }
    else {
        lo = mid+1;
    }
}
  • Vote: I like it
  • +53
  • Vote: I do not like it

»
11 years ago, # |
  Vote: I like it -27 Vote: I do not like it

Have you ever heard about binary search?

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it +40 Vote: I do not like it

    You'd normally use binary search for finding an element from an increasing sequence of values, and ternary search for finding the maximum when the values first increase and then start decreasing at some point.

    The observation here is that you can replace ternary search with a binary search for the point when the sign between adjacent values change. This is of course a simple thing, but in many places you can find the recommended solution being ternary search, which is harder to get right and less efficient.

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it -6 Vote: I do not like it

      Thanks a lot. This comment helped me to understand much more than the whole op post.

      → Reply
»
11 years ago, # |
  Vote: I like it +8 Vote: I do not like it

Does it work correctly in case f(mid) == f(mid + 1) ?

For example: f = {0, 1, 0, 0, 0}

→ Reply
  • »
    »
    11 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    No, the function should be first strictly increasing and then strictly decreasing or vice versa.

    EDIT: increasing/decreasing --> strictly increasing/decreasing

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Ok, ternary search also requires strict increase/decrease. So you algorithm is preferable.

      → Reply
»
11 years ago, # |
  Vote: I like it +8 Vote: I do not like it

Btw, if you search for some "double" answer, there is another intresting way to do that: just divide the segment by golden ratio, for example: AB → ACDB, where C divides AB in the way that AC < CB and D divides AB and AD > DB. The feature is unaware of the sub-segment you choose (AD or CB), one of the points you need on the next step is C or D; it's easy to prove from the definition of golden ratio.

So, you have to calculate only one next func value instead of two, but that can be really important in some cases, for example ones the function I minimized contained Dijkstra algorithm, so that was a cool cheat and my code easily passed TL without optimizing anything else.

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Could you please explain the algorithm in more detail? Maybe a sample code will be useful. Thanks in advance.

    → Reply
»
11 years ago, # |
  Vote: I like it +16 Vote: I do not like it

What you're doing is very similar to binary search on continuous derivative (which may be useful for some floating-point problems, because calculating derivative may be performed with more precision sometimes). If it is below zero until some point and is above zero after that point, then local optima is in the point where derivative is zero. You've calculated discrete derivative and look for a point where it changes the sign.

→ Reply
»
11 years ago, # |
  Vote: I like it 0 Vote: I do not like it

So, what you are saying is that in some cases you can just use binary instead of ternary? I couldn't understand it well. Would you mind linking me to a problem where this applies?

Thanks in advance!

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    no, he's not saying that. what he means is that it is sufficient to divide the interval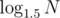 [lo,hi] into two parts, instead of three, while doing ternery search.
    the benefit is the reduction in complexity from to 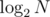. this is usually not significant, but it's a reduction nonetheless and may help for problems with tight time limits.

    → Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I don't need to take any special care with the f(mid+1)? If the search goes to the end of the data in my array for example. Actually i just got Accepted with this approach for ternary search by changing it to:

int ternary(int lo, int hi){
	while(lo <= hi){
		int mid = (lo+hi) >> 1;
		if(f(mid) > f(mid+1)){
			hi = mid-1;
		}
		else{
			lo = mid+1;
		}
	}
}
→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    If we look at it from a divide and conquer perspective, you are discarding mid at every iteration, I don't understand how this got accepted.

    The safe thing to to do with this approach is to keep a variable which keeps the maximum value of the mid.

    If f(mid)>f(mid+1), maybe the mid value found at first iteration is the actual maxima. Now you've reduced search space to [lo,mid-1] regardless. You can just add a line max_val = max(max_val,f(mid)) above it, to make it absolutely correct.

    You don't need to worry about mid+1 exceeding high in the author's code, here you've added an extra equal-to lo<**=**high , so you should take care of it.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      You're completely right. But it has been such a long time and i don't remember for which problem i have used this code. Thank you.

      → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Hi . I have got a great help from this Blog about Ternary Search . And I have applied in some problems also and got a predicted result . Now My Question is how can I use this Ternary Search for Floating Point Data ??

Thanks in advance .

→ Reply
»
6 years ago, # |
  Vote: I like it +9 Vote: I do not like it

There's a better way: Golden-section search. It reduces hi - lo by a factor of φ ≈ 1.618 by only probing one new point. For example, it can reduce 106 to 1 in around 29 calls to f, instead of 40.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it -7 Vote: I do not like it

    This post is about ternary search on integers. We can't choose integer points in the same way as we do it in golden-section search.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +8 Vote: I do not like it

      Why not? Just round it to the nearest integer each time.

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Yes, the length will be reduced by φ, but the main benefit of this search is that we calculate the function at one point on each iteration after the first. I don't think this property remains if we round the points on each iteration.

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it +12 Vote: I do not like it

          You just need to be a bit careful. Here's the code. It calls f up to 31 times.

          → Reply
          • »
            »
            »
            »
            »
            »
            6 years ago, # ^ |
              Vote: I like it +21 Vote: I do not like it

            Nice code, seems I was wrong.

            → Reply
          • »
            »
            »
            »
            »
            »
            5 years ago, # ^ |
            ← Rev. 2   Vote: I like it 0 Vote: I do not like it

            please could you update the code link,its not working

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              5 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              It was a temporary link, the code is now lost forever, sorry about that :(

              → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

But it doesn't work for the case f(mid)=f(mid+1)

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +9 Vote: I do not like it

    Ternary search doesn't work either.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Yeah you're right, didn't noticed that, but at least there are some special cases which ternary works, but this doesn't... Doesn't really matter, as I said, I was wrong...

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        Can you give such special cases? Pretty sure this works as good or better in almost any case.

        UPD: Okay apparently it is horrible for problems with real numbers. Example: http://codeforces.net/contest/1059/problem/D But for these problems ternary search is easy to code anyways (because don't have to deal with annoying cases on the integers), so this method really has no drawbacks.

        A good problem you can try this on is USACO angry cows (gold). Similar idea to the above problem, but on integers (so you can use this "trick").

        → Reply