JuanMata's blog

TopCoder SRM 616
By JuanMata, 11 years ago, In English

Today will take place TopCoder SRM 616. Wish all participants good luck and high rating!
Contest starts exactly 65 minutes from now, so register yourselves on the arena before the next hour in order to participate.

Let's discuss the problems here after the contest.

  • Vote: I like it
  • +33
  • Vote: I do not like it

»
11 years ago, # |
  Vote: I like it +2 Vote: I do not like it

How to solve Div1 250 ? Many people are failed on system test + challenge !

→ Reply
  • »
    »
    11 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    I just kept an array of the distance from original sleepiness, e.g. x0 = 0 and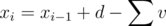 for i ≥ 1 where v are the volumes from all the alarms at time i. You only have to check the first L where L =  lcm of all the periods (though checking 2520 always suffices as well :P) The optimal starting sleepiness is max( - xi) over .

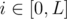    Unless xL < 0; then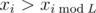 for i > L so the starting sleepiness is unbounded. If xL ≥ 0 then 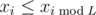for i > L so the max  - xi for i > L will be smaller.

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Why do we need to keep an array? Just simulate the process for first LCM minutes.

      → Reply
      • »
        »
        »
        »
        11 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        It is not a big deal. I always keep stuff like this in an array because I mess up a lot and need debugging ease. :)

        → Reply
  • »
    »
    11 years ago, # ^ |
    ← Rev. 3   Vote: I like it +1 Vote: I do not like it

    bli0042 has got the right approach (same as mine), but i just want to add a proof for this.

    since L is the lcm of all period[i], we can see that if any alarm rings k times in the time (0,L] then it will ring exactly k times again in the times (L,2L], (2L,3L], etc. therefore we have sleep[m*L] = m*sleep[L] for any non-negative integer m.
    now if sleep[L] < 0, we can see that the sleepiness is unbounded (can become  - ∞). therefore the answer is -1.
    otherwise it is the most negative element of the (sub)array sleep[0:L].

    → Reply
»
11 years ago, # |
  Vote: I like it +26 Vote: I do not like it

Phew, I just finished div1 1000. The solution's not very hard to think up — I tried all sorted triples of corners (306 / 6 at most) and for each one, checked if the pairs of 1st and 2nd, 1st and 3rd, 2nd and 3rd pair of L-s can intersect; then, I used the principle of inclusion-exclusion to count the number of ways in which segment lengths can be chosen so that there'd be no intersections. If you know a subset of required (and possible, e.g. no segment would have to include a black point) intersections, then it's possible to count the number of ways, but the formulas are long and so rather error-prone.

→ Reply
»
11 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

My code for 1000 Div2 got (WA) on empty matrix 20x20 (test 24). However, for maximum possible empty matrix 30x30 (test 8) is OK (as well as will other tests).

Does anybody encounter same problem?

UPD: It seems like div2 1000 != div1 500

→ Reply