triangles - Codeforces

11 years ago, # |

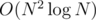Denote a right triangle as $\text{[math]}$ with the right angle at vertex $\text{[math]}$ . Try choosing each point as $\text{[math]}$ . Sort the other points by angle around it, then try choosing each point as $\text{[math]}$ (in sorted order) and use 2 pointers to keep the range of points which are at 90° to it (candidates for $\text{[math]}$ ). Time: $\text{[math]}$ due to sorting.

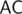Can be improved to O(N²) — if we choose $\text{[math]}$ , there are just N interesting lines (the ones perpendicular to some $\text{[math]}$ ), and we need to count the points lying on each of them; that can be achieved using hashmaps.

→ Reply

11 years ago, # ^ |

Can be improved to O(N²)

Still not so good, because of GCD calculation.

→ Reply

11 years ago, # ^ |

So, how can it be improved, maybe converting to unit vectors?

→ Reply

11 years ago, # ^ |

Well, in such a case you'll be dealing with floating-point numbers. If you want to hash them, you need to round them first. It's inherently not a very good thing.

You can still do it, but you need to calculate the needed precision for rounding first.

→ Reply

11 years ago, # ^ |

Do you have any other suggestions?

→ Reply

11 years ago, # ^ |

If you really want to do something, you can implement all of the three solutions and choose the fastest one :).

Or you can try to prove that this problem can be solved only in ω(n²) time :).

None of these ideas is really serious, though.

→ Reply

11 years ago, # ^ |

Good point. I considered the coordinates to be O(1), since they're pretty small, but even if they weren't, they're limited by int size anyways, and there's a large constant factor in the hashing solution anyways. I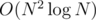 ~~estimate~~ guess that even if we had all |x| and |y| coprime, we wouldn't get a serious boost in complexity. And the $\text{[math]}$ is actually quite fast, because it stands on quicksort, which can have a really low low constant factor (in a contest, I'd code that immediately).

→ Reply

11 years ago, # ^ |

For N=5000 it seems not the optimal solution

→ Reply

11 years ago, # ^ |

Many contests in Kazakhstan are not prepared well, you must know it. There can be no maximal test cases or the solutions can be run and checked manually, ignoring the limits. So, from exactly what contest did you take this problem from?

→ Reply

http://olympiads.kz/node/53

11 years ago, # ^ |

→ Reply

11 years ago, # ^ |

It's obvious that arti's solution is exactly the same as was described by Xellos (with hashtable).

But why didn't you try just to run the solution? I've done this and the result is exactly what should have been expected: TLE (my laptop is obviously much more powerful than the judges' machines in 2008).

BTW, the solution with sorting is really faster, when implemented correctly.

→ Reply

11 years ago, # ^ |

I've also tried to run my solutions but got TL with different methods: using gcd, unit vectors and just angles, all of them give me TL. I will try to do it using quicksort, but how to be sure that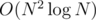 $\text{[math]}$ solution will not give TL for N = 5000?

→ Reply

11 years ago, # ^ |

← Rev. 2 →

You can't be 'sure' with anything, but you can speak from experience — some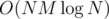 $\text{[math]}$ solutions passed 372C - Watching Fireworks is Fun. The runtime depends a lot on what the algorithm actually uses, and quicksort is... well, quick. And 2 pointers also have a low constant.

→ Reply

zeliboba

11 years ago, # ^ |

GCD could be precalculated in O(n^2) for all a,b<5000

→ Reply

11 years ago, # ^ |

They're up to 10⁴ here, but yeah, with some tricks like first few steps of GCD + precalc, that'd work pretty fast, too.

The question at this point is rather whether there's a solution that takes O(N²) when the coordinates can be arbitrarily large (provided we can do constant time arithmetics on them).

→ Reply

11 years ago, # ^ |

The question at this point is rather whether there's a solution that takes O(N²) when the coordinates can be arbitrarily large (provided we can do constant time arithmetics on them).

Such a solution does exist. I've asked a question in Russian yesterday and Igorjan94 has given me a link to an article.

→ Reply