Рассмотрим следующую задачу:
Дано корневое дерево с $$$n$$$ вершинами. В каждой вершине записан символ $$$c_v \ (1 \leq c_v \leq C)$$$, где $$$C$$$ — размер алфавита. Для каждой вершины $$$v \ (1 \leq v \leq n)$$$ требуется посчитать значение префикс функции на вертикальном пути от корня до $$$v$$$.
Наивное решение
Во время поиска в глубину будем поддерживать стек со значениями префикс функции и пересчитывать ее также, как и в стандартном варианте для 1 строки.
Вспомним, что префикс функция имеет амортизированную асимптотику, поэтому можно построить тест — кисточка, где бамбук состоит из одинаковых букв, а в листьях другие символы. Для каждого листа префикс функция будет искаться за глубину дерева, поэтому итоговая асимптотика составить $$$O (n^2)$$$.
Немного умнее
Будем считать $$$dp[v][sym]$$$ — значение префикс функции в вершине $$$v$$$, если мы перешли в нее по символу $$$sym$$$. Пересчитывать такую динамику удобнее всего лениво, используя пересчет префикс функции из стандартного алгоритма, но учитывая символ по которому перешли в вершину. Всего состояний динамики $$$n \cdot C$$$, и пересчитываются они суммарно за $$$O (n \cdot C)$$$, поэтому асимптотика будет $$$O (n \cdot C)$$$.
Что-то умное
Для удобства понимания представим переходы префикс функции как переходы автомата.
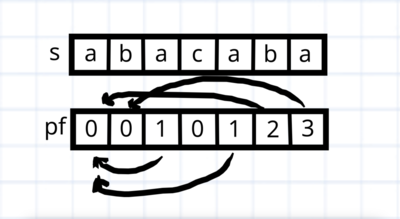
Помимо обычной префикс функции будем считать значение префикс функции, которое оканчивается на отличную от текущей букву, если переходить по переходам префикс функции. Более формально — ищем ближайший префикс после которого идет другой символ. Теперь при вычислении обычной префикс функции мы можем ходить по этим переходам и получить магическую асимптотику в $$$O (n)$$$.
Доказательство данного факта является нетривиальной задачей и остается читателям в качестве упражнения со звездочкой. Предлагается написать его в комментарии.
Задачи на эту идею:











Деда молодчинка, жду его новых крутых работ и интереснейших статей!
Разве там не будет дополнительного $$$log(n)$$$ в асимптотике? К примеру на дереве-метле?
Построим последовательность строк $$$s_{2n} = s_{2n-1} b s_{2n-1}$$$ и $$$s_{2n+1} = s_{2n} a s_{2n}$$$. Тогда получится последовательность $$$a, aba, abaaaaba, \ldots$$$. Заметим, что в последовательности $$$\pi_i, \pi_i^{(2)} = \pi[\pi_i] \ldots$$$ будет подпоследовательность с чередующимися переходами длины $$$\texttt{popcount}(i) = O(\log n)$$$. Теперь понавешаем к вершинам дерева, которые лежат на глубине с количеством битов не меньше чем $$$\frac12 \log_2 n$$$ детей по символу $$$c$$$ и поймем, что твой алгоритм отработает за $$$O(n \log n)$$$, так как таких вершин как минимум $$$\frac12 n$$$. При этом использовано всего $$$3$$$ различных символа и нет переходов по одинаковым символам.
Из хороших новостей оценка на $$$O(n \log n)$$$ переходов достигается. Ведь если обозначить $$$\mu_i$$$ как переход по супер ссылке, то будет выполняться $$$\mu_k < \frac12 k$$$ (тривиально доказывается по лемме о двух периодах).