[problem:451364A]
Idea: yazan_istatiyeh, prepared: noomaK
This problem was our way of saying hi:)
To solve the problem you can keep increasing n until it is divisible by k, this is a linear solution.
A constant solution is to find how much we need to add to n to make it divisible by k, so the solution becomes $$$x + k - (x \pmod k)$$$, or $$$(n / k + 1) * k$$$ taking advantage of integer (floor) division.
#include "bits/stdc++.h"
using namespace std;
typedef long long ll;
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int q;
cin >> q;
while (q--) {
int x, k;
cin >> x >> k;
cout << (x + (k - x % k)) << '\n';
}
}
[problem:451364B]
Idea: DeadPixel99, prepared: noomaK
We need to notice that if a player is playing with a prime or a $$$1$$$ he will lose, because he can't do any moves.
If a player has a number that's composite in his turn, he can just divide by all numbers in the divisors other than $$$1$$$ prime, guaranteeing his opponent losing.
Time complexity $$$O(\sqrt{N})$$$ for each test case.
#include "bits/stdc++.h"
using namespace std;
typedef long long ll;
#define deb(...) logger(#__VA_ARGS__, __VA_ARGS__)
template<typename ...Args>
void logger(string vars, Args&&... values) {
cout << vars << " = ";
string delim = "";
(..., (cout << delim << values, delim = ", "));
cout << '\n';
}
void solve() {
int n;
cin >> n;
for (int i = 2; i * i <= n; ++i) if (n % i == 0) {
cout << "Ahmad\n";
return;
}
cout << "Monther\n";
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t = 1;
cin >> t;
while(t--) {
solve();
}
}
[problem:451364C]
Idea: noomaK, prepared: noomaK
We firstly need to notice that greedy won't work here, because the optimal strategy might be to delete some small ones then be able to delete a large one.
Now it's obvious to see that we don't need to minimize the number of indices we fix, so we can just brute force how much to delete from the beginning of the broken bits and delete the rest from the right, and minimize in each step.
Time complexity $$$O(K + N)$$$.
#include "bits/stdc++.h"
using namespace std;
typedef long long ll;
#define deb(...) logger(#__VA_ARGS__, __VA_ARGS__)
template<typename ...Args>
void logger(string vars, Args&&... values) {
cout << vars << " = ";
string delim = "";
(..., (cout << delim << values, delim = ", "));
cout << '\n';
}
void solve() {
int n, k;
string s, t;
cin >> n >> k >> s >> t;
vector<int> a;
for (int i = 0; i < n; ++i) {
if (s[i] != t[i]) {
a.push_back(i);
}
}
int m = a.size();
k = min(m, k);
if (m == k) {
cout << 0 << '\n';
return;
}
int ans = a[m - 1] - a[0] + 1;
for (int i = 0; i <= k; ++i) {
int j = m - 1 - (k - i);
assert(a[j] >= a[i]);
ans = min(ans, a[j] - a[i] + 1);
}
cout << ans << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t = 1;
// cin >> t;
while(t--) {
solve();
}
}
[problem:451364D]
Idea: noomaK, prepared: noomaK
Notice that for every unique middle string, there can only be $$$O(K^2)$$$ unique pairs of (first_character, last_character). Where $$$K$$$ is the size of the alphabet, which is $$$26$$$ in this problem.
Let $$$m$$$ be the number of pairs for some middle string, then we can get the answer for every middle string by brute forcing all pairs of pairs in $$$O(m^4)$$$.
Why does this work and not TLE? The worst case for our brute force is obviously $$$O(K^4)$$$, how many times will this occur in our input? $$$O(N / (K^2))$$$ which is not much.
So it passes.
#include "bits/stdc++.h"
using namespace std;
typedef long long ll;
#define deb(...) logger(#__VA_ARGS__, __VA_ARGS__)
template<typename ...Args>
void logger(string vars, Args&&... values) {
cout << vars << " = ";
string delim = "";
(..., (cout << delim << values, delim = ", "));
cout << '\n';
}
void solve() {
int n;
cin >> n;
map<string, vector<pair<int, int>>> mp;
for (int i = 0; i < n; ++i) {
string s;
cin >> s;
mp[s.substr(1, (int)s.size() - 2)].push_back({s[0] - 'a', s.back() - 'a'});
}
int ans = 0;
for (auto [s, v] : mp) {
sort(v.begin(), v.end());
v.erase(unique(v.begin(), v.end()), v.end());
for (int i = 0; i < (int)v.size(); ++i) {
for (int j = i + 1; j < (int)v.size(); ++j) {
ans = max(abs(v[i].first - v[j].first) + abs(v[i].second - v[j].second), ans);
}
}
}
cout << ans << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t = 1;
// cin >> t;
while (t--) solve();
}
Solve for bigger $$$K$$$ (bigger alphabet).
[problem:451364E]
Idea: noomaK, prepared: yazan_istatiyeh
Connecting and disconnecting roads gives a hint to using DSU, also finding the minimum number of coins gives a hint to binary search.
The first thing we notice is that blocking all roads would be valid, now to construct the solution, we will use binary search on the answer, it will work because if we blocked all roads that cost $$$X$$$ or less and it was valid, blocking all roads that cost $$$X + 1$$$ or less would be valid too.
So for each midpoint in the binary search, we can check if the current cost is valid or not by connecting components in DSU when an edge cost is more than the current cost we are checking (the more we block the better, so we should not be choosy about what to block or not, if we can block a road then it is either would not change anything or it would disconnect two cities from each other), after that, we can check for connectivity for all forbidden pairs (cities in feuds), if all pairs were disconnected, then the current cost is valid and we search for less, if not, the current cost is invalid and we should search for a higher cost.
Solution Complexity: $$$O(log_2(10 ^ 9) * m * log_2(n))$$$
#include "bits/stdc++.h"
using namespace std;
typedef long long ll;
class UnionFind {
private:
vector<int> p, rank, setSize;
int numSets;
public:
UnionFind(int N) {
p.assign(N, 0);
for (int i = 0; i < N; i++) {
p[i] = i;
}
rank.assign(N, 0);
setSize.assign(N, 1);
numSets = N;
}
int findSet(int i) {
return (p[i] == i) ? i : (p[i] = findSet(p[i]));
}
bool isSameSet(int i, int j) {
return findSet(i) == findSet(j);
}
int numDisjointSets() {
return numSets;
}
int sizeOfSet(int i) {
return setSize[findSet(i)];
}
void unionSet(int i, int j) {
if (isSameSet(i, j)) return;
int x = findSet(i), y = findSet(j);
if (rank[x] > rank[y]) swap(x, y);
p[x] = y;
if (rank[x] == rank[y]) rank[y]++;
setSize[y] += setSize[x];
numSets--;
}
};
struct Edge {
int u, v, t;
Edge(int u, int v, int t): u(u), v(v), t(t) {}
};
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int n, m, k;
cin >> n >> m >> k;
vector<Edge> edges;
for (int i = 0; i < m; i++) {
int u, v, t;
cin >> u >> v >> t;
u--, v--;
edges.emplace_back(u, v, t);
}
vector<pair<int, int>> feuds(k);
for (auto &[u, v]: feuds) {
cin >> u >> v;
u--, v--;
}
auto check = [&](int x) {
UnionFind dsu(n);
for (auto [u, v, t]: edges) {
if (t > x) dsu.unionSet(u, v);
}
for (auto [u, v]: feuds) {
if (dsu.isSameSet(u, v)) {
return false;
}
}
return true;
};
int l = 0, r = 1e9, ans = 1e9;
while (l <= r) {
int mid = l + (r - l) / 2;
if (check(mid)) {
ans = mid;
r = mid - 1;
} else {
l = mid + 1;
}
}
cout << ans;
}
[problem:451364F]
Idea: yazan_istatiyeh & noomaK, prepared: yazan_istatiyeh
The first thing we notice is that $$$cost(s, t) = |s| + |t| - 2 * LCP(s, t)$$$, where $$$|s|$$$ is the length of the string $$$s$$$, and $$$LCP(s, t)$$$ is the longest common prefix between s and t.
Calculating |s| and |t| for all pairs is trivial since each string would be in a pair $$$2 * n - 1$$$ times, we can add $$$(2 * n - 1) * |s|$$$ to our answer, for each string.
Now we have to calculate LCP over all pairs, this can be done using trie & dfs.
We can see that on the trie, the LCP between 2 strings is the LCA (lowest common ancestor) between them, we can use this fact to calculate our answer, so for each node in the trie (looking at it from the bottom to the top), some strings would meet, these strings' LCP will be the node's depth, the following illustration of the example will explain more, we will try to calculate the total LCP for it.
For each node in the trie, we need to add to our total LCP the number of pairs of strings (terminal nodes) meeting on that node multiplied by the depth of that node, this will become more clear now.
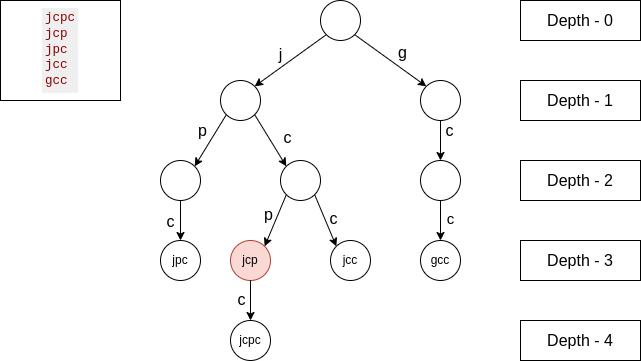
In a trie, (hypothetically) each node has 26 edges, in the highlighted node above, one string ends on it and there is one string coming from a node, so we will add $$$countOnNode * countFromEdge * nodeDepth$$$ to our total LCP, which is $$$1 * 1 * 3 = 3$$$, where node depth is actually the between all strings meeting on that node.
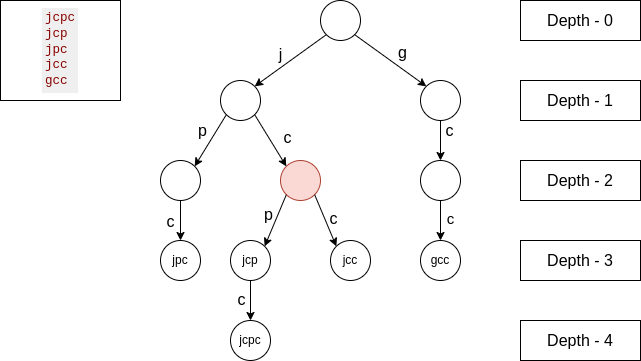
In the new highlighted node, from an edge, we have 2 strings, from another edge we have 1 string, all other edges have 0 strings. So we will add to the total LCP the following, $$$cntFromFirst_edge * countFromSecondEdge * nodeDepth$$$, which is $$$2 * 1 * 2$$$.

In the new highlighted node, from an edge we have 1 string, from another edge we have 3 strings, so we will add $$$1 * 3 * 1$$$ to the total LCP.
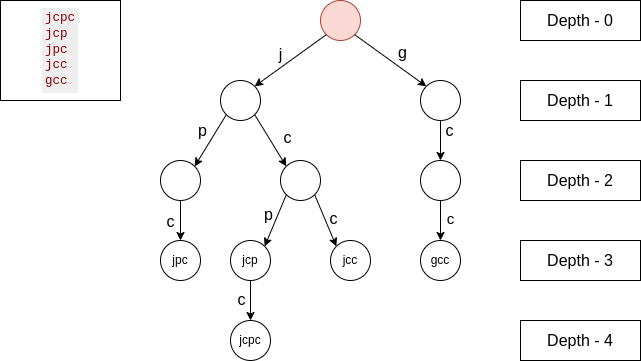
In the new highlighted node, which is the root that has $$$depth = 0$$$, from an edge we have 1 string, from another edge we have 4 strings, so we will add $$$1 * 4 * 0$$$ to the total LCP.
Now our total answer is $$$3 + 4 + 3 + 0 = 10$$$, which is the total LCP, but for unordered pairs, so we will multiply it by 2 to get it for ordered pairs, also, we must not forget about the pairs of strings with itself, which has $$$LCP = |s|$$$, so we must add the strings lengths to the total LCP.
Now we have to multiply the total LCP by 2 from our original equation $$$|s| + |t| - 2 * LCP(s, t)$$$.
So finally we will subtract the total LCP from our sum of lengths, and we will get the answer:)
Solution Complexity: $$$O(\sum |s| * 26)$$$
The solution uses trie with pointers, by yazan_istatiyeh:
#include "bits/stdc++.h"
using namespace std;
typedef long long ll;
class Trie {
private:
struct Node {
char alphabet;
bool exist; // or end of word, or count of words
int cnt;
vector<Node*> child;
Node(char a): alphabet(a), exist(false), cnt(0) {
child.assign(26, NULL);
}
};
Node* root;
public:
Trie() {
root = new Node('!');
}
void insert(string word) {
Node* cur = root;
for (int i = 0; i < (int) word.size(); i++) {
int alphaNum = word[i] - 'a';
if (cur -> child[alphaNum] == NULL) {
cur -> child[alphaNum] = new Node(word[i]);
}
cur = cur -> child[alphaNum];
}
cur -> exist = true;
}
ll getAns() {
function<void(Node*)> dfs = [&](Node* node) {
node->cnt = node->exist;
for (auto next: node->child) {
if (next != NULL) {
dfs(next);
node->cnt += next->cnt;
}
}
};
dfs(root);
ll ret = 0;
function<void(Node*, int)> calc = [&](Node* node, int depth) {
ll pre = 0;
for (int i = 0; i < 26; i++) {
if (node->child[i] == NULL) continue;
auto &next = node->child[i];
ret += node->exist * depth * next->cnt;
ret += pre * depth * next->cnt;
pre += next->cnt;
calc(next, depth + 1);
}
};
calc(root, 0);
return ret;
}
};
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int n;
cin >> n;
Trie trie;
ll ans = 0;
for (int i = 0; i < n; i++) {
string s;
cin >> s;
trie.insert(s);
ans += (2ll * n - 2) * s.size();
}
ans -= trie.getAns() * 4;
cout << ans;
}
This solution uses trie with normal arrays, by noomaK:
#include "bits/stdc++.h"
using namespace std;
typedef long long ll;
const int N = 1e6 + 1;
const int K = 26;
int trie[N + 2][K];
int sub[N + 5];
int tc;
void insert(const string &s) {
int n = s.size();
int root = 0;
for (int i = 0; i < n; ++i) {
int j = s[i] - 'a';
if (!trie[root][j]) {
trie[root][j] = ++tc;
}
root = trie[root][j];
}
sub[root] += 1;
}
ll ans;
string cr;
void dfs(int u, int d = 0) {
ll cur = sub[u], sum = 0;
string t = cr;
for (int j = 0; j < 26; ++j) if (trie[u][j]) {
int v = trie[u][j];
dfs(v, d + 1);
sub[u] += sub[v];
sum += cur * sub[v];
cur += sub[v];
}
ans -= d * 4ll * sum;
}
void solve() {
int n;
cin >> n;
ans = tc = 0;
for (int i = 0; i < n; ++i) {
string s;
cin >> s;
insert(s);
ans += (n - 1) * 2ll * (int)s.size();
}
dfs(0);
cout << ans << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t = 1;
// cin >> t;
while(t--) {
solve();
}
}
An alternative solution using hashing, by Eyd
#include "bits/stdc++.h"
using namespace std;
using ll = long long;
struct dat{
int in_len;
int ex_len;
int num;
};
const int M = 1e9 + 7;
const int bs = 301;
const int M2 = 1e9 + 123;
const int bs2 = 31;
void solve(){
int n;
cin >> n;
vector<string> g(n);
for(auto&x : g)cin >> x;
map<pair<int, int>, dat> fr;
int total_len = 0;
for(int i = 0; i < n; i++){
// string a = "";
int a = 0;
int pw = 1;
int b = 0;
int pw2 = 1;
total_len += g[i].size();
for(int j = 0; j < g[i].size(); j++){
(a += pw * (g[i][j] — '0')) %= M;
(pw *= bs) %= M;
(b += pw2 * (g[i][j] — '0')) %= M2;
(pw2 *= bs2) %= M2;
fr[{a, b}].num++;
fr[{a, b}].ex_len += g[i].size()-j-1;
fr[{a, b}].in_len += g[i].size()-j;
}
}
ll ans = 0;
for(int i = 0; i < n; i++){
ll tot = total_len;
ll num = n;
int a = 0;
int b = 0;
int pw = 1;
int pw2 = 1;
for(int j = 0; j <= g[i].size(); j++){
(a += pw * (g[i][j] — '0')) %= M;
(pw *= bs) %= M;
(b += pw2 * (g[i][j] — '0')) %= M2;
(pw2 *= bs2) %= M2;
dat d = fr[{a, b}];
ans += (tot — d.in_len) + (g[i].size()-j)*abs(num-d.num);
tot = d.ex_len;
num = d.num;
}
}
cout << ans;
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
int t = 1;
// cin >> t;
while(t--){
solve();
cout << '\n';
}
return 0;
}
[problem:451364G]
Idea: noomaK, prepared: noomaK
What if there was only two numbers in the list?
Bézout's Identity
Do we need to check every subset of the list if there is more than 2 numbers ?
First, let's use Bézout's Identity or The Extended Euclidean Algorithm, to know that for any two numbers $$$x$$$ and $$$y$$$, we can reach any multiple of their $$$gcd$$$.
Now we can generalize this to see that we need a subset of our list with a $$$gcd$$$ that divides $$$k$$$ in our third query, but getting a subset with some $$$gcd$$$ isn't a trivial task.
We can prove that it's sufficient to just check for the $$$gcd$$$ of the whole list.
Why? Because let the $$$gcd$$$ for some subset be $$$g′$$$ and $$$g'$$$ divides $$$k$$$, and $$$g$$$ the $$$gcd$$$ of the list, we can see that $$$g$$$ is a divisor of $$$g′$$$ therefore $$$g$$$ also divides $$$k$$$.
Now we just need a way to get the $$$gcd$$$ of a changing list, we use some data structures like Segment Tree for example.
Time complexity $$$O(qlog_2(A)log_2(q))$$$, $$$A$$$ is the maximum number in the list.
#include "bits/stdc++.h"
using namespace std;
typedef long long ll;
#define deb(...) logger(#__VA_ARGS__, __VA_ARGS__)
template<typename ...Args>
void logger(string vars, Args&&... values) {
cout << vars << " = ";
string delim = "";
(..., (cout << delim << values, delim = ", "));
cout << '\n';
}
const int N = 2e5;
int tree[N * 2 + 2];
void up(int i, int x) {
for (tree[i += N] = x; i > 1; i >>= 1) {
tree[i >> 1] = gcd(tree[i], tree[i ^ 1]);
}
}
void solve() {
int q;
cin >> q;
map<int, int> last, freq;
for (int i = 0; i < q; ++i) {
int t, x;
cin >> t >> x;
if (t == 1) {
if (!last.count(x)) last[x] = i;
if (++freq[x] == 1) {
up(i, x);
}
} else if (t == 2) {
if (--freq[x] == 0) {
up(last[x], 0);
last.erase(x);
}
} else {
int g = tree[1];
if (g > 0 && x % g == 0) {
cout << "YES\n";
} else {
cout << "NO\n";
}
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t = 1;
// cin >> t;
while(t--) {
solve();
}
}
We hope you enjoyed the contest and benefited from it, and would love to hear your feedback:)










Nice Problem-set guys. <3
Excited for the next rounds,thx for the preparers
Maximum manhattan distance can be calculated in $$$O(k)$$$ for $$$k$$$ given points in the problem D. My Submission
interesting problems and very good tutorial, well done guys.
good collection of problems keep coding!
Can you please open the solutions ?
Nice problems set :3
Good Problem-set. Waiting for next round
In F. The solution by noomaK. I don't understand why we're multiplying by 4 instead of 2 in the step:
ans -= d * 4ll * sum;2 from the original equation, and 2 cuz the pairs are unordered so we multiply by 2 to make them ordered.
Oh okay, thanks
not able to understand F editorial can anyone explain better how to find lcp over all pairs using trie
Let's imagine the trie as graph, for any two string their lcp node is the lca of the two nodes that represents their final character.
Knowing that, now we need to count for every node in the trie how many pairs this node is the lca.
For a node $$$u$$$ to be the lca of two nodes $$$a$$$ and $$$b$$$, $$$a$$$ and $$$b$$$ should be in the subtree of $$$u$$$ and $$$a$$$ should be in a subtree of a different child of $$$u$$$ than $$$b$$$.
To count the number of pairs for each node, we can traverse the children of $$$u$$$ in any order and keep the count of terminal nodes we've seen so far in other subtrees other than this child, and add the contribution from this child with other visited children.