Many thanks to miaowtin and FBI for their invaluable help and support in the preperation of this blog. Unfortunately, this blog is not currently completed, but we encourage everybody to share their solutions to these and other problems of the section in comments. And last but not least thanks to pllk for maintaining CSES.
Greedy
Consider the string $$$s=s_1,\dots,s_n$$$. Suppose $$$s_i$$$ is the first occurence of a letter $$$c$$$ (the string looks $$$s_1,\dots,s_i,\dots,s_n$$$). If we output $$$c$$$, the problem reduces to $$$s=s_{i+1},\dots,s_n$$$. The number of such outputs must be minimalized.
Observation: the largest $$$i$$$ we choose, the smallest string we obtain.
Greedy solution is always to take the largest $$$i$$$ such that $$$s_i$$$ is the first occurence. But after this traversal, the string we output is still a subsequence of $$$s$$$, so we need to output one more letter.
#include<bits/stdc++.h>
using namespace std;
int main()
{
string s;cin>>s;
map<char,bool>used;
for(auto&c:s)
{
used[c]=1;
if(used.size()==4)
{
cout<<c;
used.clear();
}
}
if(!used['A'])cout<<'A';
else if(!used['C'])cout<<'C';
else if(!used['G'])cout<<'G';
else cout<<'T';
}
BFS
The number of permutations of the grid is $$$9!=362880$$$. We can precalculate the answer for each case.
Let's make a graph, where each vertex is a grid. And there will be an edge between vertices $$$A$$$ and $$$B$$$, if we can make one operation on $$$A$$$ and get $$$B$$$.
The answer for
is obviously $$$0$$$.
We can run BFS starting from this grid and get all the answers.
In practice, we can maintain each grid as an integer. For example the starting grid is $$$123456789$$$. Notice that we can still maintain the required operations using the integer.
#include<bits/stdc++.h>
using namespace std;
int pw[10];
int get(int x,int i)
{
return x/pw[i]%10;
}
int f(int x,int i,int j)
{
i=9-i,j=9-j;
int di=get(x,i),dj=get(x,j);
return x+pw[j]*(di-dj)+pw[i]*(dj-di);
}
int main()
{
pw[0]=1;
for(int i=1;i<10;i++)pw[i]=pw[i-1]*10;
unordered_map<int,int>d;
queue<int>q;
q.push(123456789);
d[123456789]=0;
while(!q.empty())
{
int x=q.front();
q.pop();
for(int i=1;i<=8;i++)
{
if(i%3==0)continue;
int y=f(x,i,i+1);
if(d.find(y)==d.end())
{
d[y]=d[x]+1;
q.push(y);
}
}
for(int i=1;i<=6;i++)
{
int y=f(x,i,i+3);
if(d.find(y)==d.end())
{
d[y]=d[x]+1;
q.push(y);
}
}
}
int x=0;
for(int i=8;i>=0;i--)
{
int a;cin>>a;
x+=pw[i]*a;
}
cout<<d[x]<<"\n";
}
Tree theory
Let's define the Prüfer Code as $$$P=p_1,\dots,p_{n-2}$$$.
Feature of the Prüfer Code: if the given tree is $$$G$$$, and its Prüfer Code is $$$p_1,\dots,p_{n-2}$$$, after removing the leaf from $$$G$$$ with the smallest label, the code will be $$$p_2,\dots,p_{n-2}$$$.
That means, that after removing the leaf, we get the same problem with smaller Prüfer Code.
The integers that are missing in $$$P$$$ are leaves. Thats because the Prüfer Code is constructed is such a way, that it never contains the leaves of the tree.
Suppose we are proccessing $$$p_i$$$. There exist two cases:
- We take the leaf with the smallest label that is connected with $$$p_i$$$ and delete the it.
- We take the leaf with the smallest label that is connected with $$$p_i$$$ and delete the it. After what $$$p_i$$$ becomes a leaf.
In the second case $$$p_i$$$ becomes a leaf if $$$p_{i+1},\dots,p_{n-2}$$$ does not contain $$$p_i$$$. It follows from the feature.
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n;cin>>n;
vector<int>p(n-2),cnt(n+1);
for(auto&x:p)
{
cin>>x;
cnt[x]++;
}
set<int>leaves;
for(int v=1;v<=n;v++)
{
if(cnt[v]==0)leaves.insert(v);
}
for(auto&x:p)
{
auto it=leaves.begin();
cout<<*it<<' '<<x<<"\n";
leaves.erase(it);
if(--cnt[x]==0)leaves.insert(x);
}
cout<<*leaves.begin()<<' '<<*leaves.rbegin()<<"\n";
}
Graph theory
I assume, that if all the edges are directed from smaller vertex to largest one, the graph is acyclic.
Proof:
Suppose, such graph consists a cycle.
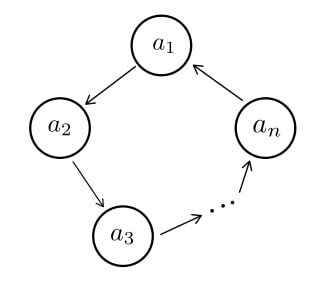
$$$a_1,\dots,a_n$$$ is a subset of vertices which forms a cycle.
$$$a_1 < a_2 < a_3< \dots <a_n < a_1$$$, because we construct the graph in such way. As you can notice, this expression is impossible.
#include<iostream>
using namespace std;
int main()
{
int n,m;cin>>n>>m;
for(int i=0;i<m;i++)
{
int u,v;cin>>u>>v;
if(u>v)swap(u,v);
cout<<u<<' '<<v<<"\n";
}
}
Binary search
Let $$$F(k)$$$ is the amount of integers in the table with values $$$\le k$$$.
To calculate this function we can proccess each row seperately. $$$x$$$-th row contains integers $$$x,2x,\dots,nx$$$. There are $$$\min(n,\lfloor\frac{k}{x}\rfloor)$$$ integers from this list which are not greater than $$$k$$$.
To get the answer we need to find such maximal $$$k$$$, that $$$F(k)\le \lceil{\frac{n^2}{2}}\rceil$$$. Notice, the function is non-decreasing, hence we can use binary search.
#include<iostream>
typedef long long ll;
using namespace std;
ll n;
bool F(ll k)
{
ll s=0;
for(int x=1;x<=n;x++)s+=min(n,k/x);
return s<n*n/2+1;
}
int main()
{
cin>>n;
ll l=1,r=n*n;
while(r-l>1)
{
ll mid=(l+r)/2;
if(F(mid))l=mid;
else r=mid;
}
cout<<r<<"\n";
}
Monotonic stack
Let's fix the height of the rectangular. The high can be any of the boards, so let's consider $$$k_i (1\le i\le n)$$$.
The idea is that we can extend this rectangular to the left and right, while the heights are not less than $$$k_i$$$. Formally, the problem is to find:
- The minimal $$$l$$$, that $$$1\le l\le i$$$ and $$$\min(k_l,\dots,k_i)\ge k_i$$$.
- The maximal $$$r$$$, that $$$i\le r \le n$$$ and $$$\min(k_i,\dots,k_r)\ge k_i$$$.
If we found such $$$l,r$$$ for fixed $$$i$$$, the area of the rectangular is $$$k_i \cdot (r-l+1)$$$.
Let's maintain a stack which contains the positions $$$p_1,\dots,p_m$$$ such that $$$k_{p_1} \le \dots, \le k_{p_m}$$$. When we want to push $$$i$$$ to the stack, the condition of monotonic elements must be still met. So we need to pop the elements from the stack while $$$k_i \le k_{p_m}$$$. The advantage of such stack is that after erasing the positions, $$$k_{p_m}$$$ will always be the first element less than $$$k_i$$$. So the $$$l$$$ we need in the problem is $$$p_m+1$$$.
The idea of finding $$$r$$$ is symmetric.
#include<bits/stdc++.h>
using namespace std;
const int N=200005;
int k[N],l[N],r[N];
int main()
{
int n;cin>>n;
for(int i=1;i<=n;i++)cin>>k[i];
stack<int>s;
for(int i=1;i<=n;i++)
{
while(!s.empty()&&k[s.top()]>=k[i])s.pop();
if(s.empty())l[i]=1;
else l[i]=s.top()+1;
s.push(i);
}
while(!s.empty())s.pop();
for(int i=n;i>=1;i--)
{
while(!s.empty()&&k[s.top()]>=k[i])s.pop();
if(s.empty())r[i]=n;
else r[i]=s.top()-1;
s.push(i);
}
long long mx=0;
for(int i=1;i<=n;i++)mx=max(mx,1ll*k[i]*(r[i]-l[i]+1));
cout<<mx<<"\n";
}
Prefix sums
Suppose, the string contains the characters $$$c_1,c_2,\dots,c_k$$$. The first idea is to make $$$k$$$ prefix sums, where each of them responds for each character.
Now the substring $$$[l,r]$$$ is special iff $$$P_{r,ch}-P_{l-1,ch}$$$ is equal to $$$x$$$ where $$$ch$$$ is one of $$$c_1,\dots,c_k$$$.
Notice that if the string is special, than all the elements from $$$P_r$$$ are not less than $$$x$$$. So let's substract $$$x$$$ from $$$P_r$$$. The problem is, that we have no $$$x$$$, but we can substract the minimal value from $$$P_r$$$, bacause it is the largest $$$x$$$ we can choose.
The task is reduced to finding the number of such $$$1\le l\le r\le n$$$, that $$$P_r=P_{l-1}$$$, what can be done in $$$O(n\cdot k)$$$ time.
#include<bits/stdc++.h>
using namespace std;
int main()
{
string s;cin>>s;
map<char,int>h;
int k=0;
for(auto&c:s)
{
if(!h.count(c))h[c]=k++;
}
map<vector<int>,int>cnt;
vector<int>P(k);
cnt[P]=1;
long long ans=0;
for(auto&c:s)
{
P[h[c]]++;
int mx=*max_element(P.begin(),P.end());
for(auto&a:P)a-=mx;
ans+=cnt[P]++;
}
cout<<ans<<"\n";
}
Trie, Bitmasks
Trie is a structure which can maintain various operations with string, some basics are:
- add string $$$s$$$ to the list;
- remove string $$$s$$$ from the list;
- find a string from the list, which has the longest common prefix with $$$s$$$.
The idea is to maintain a tree where each vertex represents the ending character of some prefix and there is an edge between vertices if the next vertex continues the previous vertex' prefix. Moreover, a path from the root to some vertex is the same for two strings with same prefix.
Sometimes, it is useful to look at integers as at binary strings and process them using Trie.
More about trie you can read here.
At first, let's construct new array $$$a$$$ where $$$a_i=a_{i-1}\oplus x_i$$$. Now $$$x_l \oplus \dots \oplus x_r$$$ is equal to $$$a_r \oplus a_{l-1}$$$.
We can add the integers to a list and for each $$$a_r$$$ find optimal $$$a_{l-1}$$$. It can be done using Trie. It will contain integers in binary representation from the most significant bit.
Suppose we process $$$k$$$-th bit of $$$a_r$$$. If the trie contain the oposite bit from $$$k$$$-th, we can go to that subtree and improve the answer (because their xor gives $$$1$$$). Such improvement leads to correct answer because number comparison depends on the most significant bit.
#include<iostream>
using namespace std;
const int N=200005;
int T[N*30][2],t;
void upd(int x)
{
for(int k=29,v=0;k>=0;k--)
{
bool c=(x>>k)&1;
if(!T[v][c])T[v][c]=++t;
v=T[v][c];
}
}
int get(int x)
{
int ans=0;
for(int k=29,v=0;k>=0;k--)
{
bool c=(x>>k)&1;
if(T[v][c^1])ans|=1<<k,v=T[v][c^1];
else v=T[v][c];
}
return ans;
}
int main()
{
int n;cin>>n;
int x=0,mx=0;
upd(x);
for(int i=1,a;i<=n;i++)
{
cin>>a;
x^=a;
mx=max(mx,get(x));
upd(x);
}
cout<<mx<<"\n";
}
Binary jumping
The greedy solution is to jump to the nearest end of the movie everytime while it possible. So let's generalize this idea.
Consider a function $$$up(k,i)$$$ returns the position $$$j$$$, when we do $$$2^k$$$ greedy jumps from position $$$i$$$.
The transitions are:
because the jump of length $$$2^k$$$ can be represented as two smaller jumps of length $$$2^{k-1}$$$.
To find the answer for a query $$$[l,r]$$$ we can start from the largest $$$k$$$ trying to make the longest jump and still be in the range. And if it is possible we perform this jump and add to the answer $$$2^k$$$.
In practice, it is better to do it backwards, jumping from $$$r$$$ to $$$l$$$. The problems are equal but the implementation is a bit easier.
#include<bits/stdc++.h>
using namespace std;
const int maxB=1000002;
int up[18][maxB];
int main()
{
int n,q;cin>>n>>q;
for(int i=0;i<n;i++)
{
int l,r;cin>>l>>r;
up[0][r]=max(up[0][r],l);
}
for(int i=2;i<maxB;i++)
{
up[0][i]=max(up[0][i],up[0][i-1]);
}
for(int k=1;k<18;k++)
{
for(int i=1;i<maxB;i++)
{
up[k][i]=up[k-1][up[k-1][i]];
}
}
while(q--)
{
int l,r;cin>>l>>r;
int ans=0;
for(int k=17;k>=0;k--)
{
if(up[k][r]>=l)
{
ans|=(1<<k);
r=up[k][r];
}
}
cout<<ans<<"\n";
}
}
Bright mind
We trace the work of Euclid's algorithm for two coprime integers $$$a,b$$$
by writing '1' to a string if the second case and '0' in the third case. For example, for $$$a, b = 7, 5$$$, the string is $$$1001$$$. We denote this string by $$$trace(a,b)$$$.
Let us examine the construction of $$$trace(a,b)$$$ in terms of a number of distinct subsequences. By symmetry, we can only consider $$$cnt_1(trace(a,b)) = $$$ the number of distinct subsequences starting with $$$1$$$ (including empty string $$$\varnothing$$$) in $$$trace(a,b)$$$. We have
Taking $$$cnt_1(\varnothing)=cnt_0(\varnothing)=1$$$, we inductively obtain $$$cnt_1(trace(a,b))=a$$$ and $$$cnt_0(trace(a,b))=b$$$. So, the number of distinct subsequences in $$$trace(a,b)$$$ is $$$a+b-1$$$.
On the other hand, we can easily see that any binary string can be written via $$$trace(a,b)$$$ for some $$$a,b$$$ (just perform the algorithm backwards). Therefore, we have a bijection the set of binary strings with exactly $$$n$$$ subsequences (including the empty one) and the set of binary strings generated by $$$trace(a,b)$$$ for $$$a+b-1=n$$$.
The solution to the problem is easy now if one notices that we can iterate over the strings with exactly $$$n$$$ distinct subsequences. Go over $$$a$$$ and take $$$b=n-a+1$$$, then request $$$(a,b)=1$$$ and obtain $$$(a,n+1)=1$$$. In other words, the algorithm is the following.
- Increment $$$n$$$ by 1 (to eliminate empty substring).
- Iterate over $$$a$$$ coprime with $$$n+1$$$.
- Take $$$b=n-a+1$$$ and relax $$$trace(a,b)$$$.
#include<bits/stdc++.h>
using namespace std;
string trace(int a,int b)
{
if(a==b)return "";
else if(a>b)return '1'+trace(a-b,b);
else return '0'+trace(a,b-a);
}
int trace_len(int a,int b)
{
if(a==b)return 0;
else if(a>b)return 1+trace_len(a-b,b);
else return 1+trace_len(a,b-a);
}
int main()
{
int n;cin>>n;
int b,mn=++n;
for(int a=1;a<=n+1;a++)
{
if(__gcd(a,n+1)!=1)continue;
int len=trace_len(a,n-a+1);
if(len<mn)mn=len,b=n-a+1;
}
cout<<trace(n-b+1,b)<<"\n";
}
Greedy
See example 2 in.
FFT
First of all, we evaluate $$$p_n = $$$ the number of ones among $$$s_1, \dots, s_{n - 1}$$$ and $$$p_0 = 0$$$. Then, the naїve algorithm is the following:
- iterate $$$i, j$$$ over $$$0, 1, 2, \dots, n$$$ and increment $$$cnt[p_i - p_j]$$$,
- output $$$(cnt[0] - (n+1))/2$$$ (because we counted $$$i=j$$$ and $$$i\neq j$$$ twice) and $$$cnt[1], \dots, cnt[n]$$$.
The complexity of this algorithm is $$$O(n^2)$$$, which is not fast enough to solve the problem. Instead, we shall do the trick.
Consider the following expression
and it can be easily seen that the coefficient at $$$x^{k}$$$ is the number of pairs $$$(i, j)$$$ such that $$$p_i-p_j=k$$$, that is $$$cnt[k]$$$. As $$$p_n$$$ is the largest among $$$p_1,\dots,p_n$$$, we can make the second factor a polynomial multiplying the whole expression $$$P_{aux}$$$ by $$$x^{p_n}$$$
Then we multiply these two polynomials using FFT, and output the desired coefficients with respect to our shift by $$$x^{p_n}$$$.
#include<bits/stdc++.h>
using namespace std;
namespace FFT
{
typedef complex<double>base;
double PI=acos(-1);
void fft(vector<base>&a,bool invert)
{
int n=a.size();
for(int i=1,j=0;i<n;i++)
{
int bit=n>>1;
for(;j>=bit;bit>>=1)j-=bit;
j+=bit;
if(i<j)swap(a[i],a[j]);
}
for(int len=2;len<=n;len<<=1)
{
double ang=2*PI/len*(invert?-1:1);
base wlen(cos(ang),sin(ang));
for(int i=0;i<n;i+=len)
{
base w(1);
for(int j=0;j<len/2;j++)
{
base u=a[i+j],v=a[i+j+len/2]*w;
a[i+j]=u+v;
a[i+j+len/2]=u-v;
w*=wlen;
}
}
}
if(invert)
{
for(int i=0;i<n;i++)a[i]/=n;
}
}
vector<long long>multiply(vector<int>&a,vector<int>&b)
{
vector<base>fa(a.begin(),a.end()),fb(b.begin(),b.end());
int n=1;
while(n<max(a.size(),b.size()))n<<=1;
n<<=1;
fa.resize(n),fb.resize(n);
fft(fa,0),fft(fb,0);
for(int i=0;i<n;i++)fa[i]*=fb[i];
fft(fa,1);
vector<long long>res;
res.resize(n);
for(int i=0;i<n;i++)res[i]=(long long)(fa[i].real()+0.5);
return res;
}
};
int main()
{
string s;cin>>s;
int n=s.size();
vector<int>p(n+1),a(n+1),b(n+1);
for(int i=1;i<=n;i++)p[i]=p[i-1]+s[i-1]-'0';
for(int i=0;i<=n;i++)a[p[i]]++;
for(int i=0;i<=n;i++)b[p[n]-p[i]]++;
auto Paux=FFT::multiply(a,b);
cout<<(Paux[p[n]]-(n+1))/2<<' ';
for(int i=p[n]+1;i<=p[n]+n;i++)cout<<Paux[i]<<' ';
}











can i solve this problems as a Newibe ? is it hard for me or good?
pls help , i don't want to waste time
while(true){ thx++;}
I personally struggle with most of them.
Binary Subsequences is mindblowing! Thanks for the solution.
Regarding tutorial to Multiplication Table, how can you prove that the answer is always in the multiplication table? Because solution doesn't check for that.
Let $$$\texttt{med}=\lceil\frac{n^2}{2}\rceil$$$ the position of the element in the table we are looking for.
Then we find such $$$x$$$ that $$$F(x)<\texttt{med}$$$ and $$$F(x+1)=\texttt{med}$$$, what guarantees that $$$x+1$$$ is present in the table (otherwise we would still have $$$F(x+1)<\texttt{med}$$$).
Thank you.