if we know log(a) and log(b) how we can find log(a+b) approximately to real value?
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 166 |
| 2 | maomao90 | 163 |
| 2 | Um_nik | 163 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 160 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | nor | 153 |
| 9 | Dominater069 | 153 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Nov/18/2024 00:52:21 (h1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











log(exp(log(a))+exp(log(b)))
If a and b are close numbers, you can approximate using the following formula:
For example, if a = b, then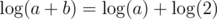
why and
and  need to be close for this formula to work?
need to be close for this formula to work? 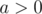 (in addition to
(in addition to 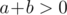 , ofcourse) sufficient?
, ofcourse) sufficient?
isn't
This formula works OK, but if is some small number, you can remember its logarithm and thus approximate
is some small number, you can remember its logarithm and thus approximate 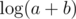 without calculator or paper — that was the point.
without calculator or paper — that was the point.
ah i see what u mean. thanks! :)