ammar_hammoud's blog

Calculating Combinations
By ammar_hammoud, history, 17 months ago, In English

Hello CF community, I'm trying to solve this problem, the problem tells me that I have to calculate

$$$C_n^r = \frac{N!}{M!\cdot (N-M)!}; 5\leq N\leq 100, M\leq N$$$

in the numerator it will always be $$$\prod _{i = N-M+1}^{n} i$$$ and in the denominator will be $$$ \prod _{i=1}^{min(N, N-M)}i$$$ as the rest will cancel out
and this is my code: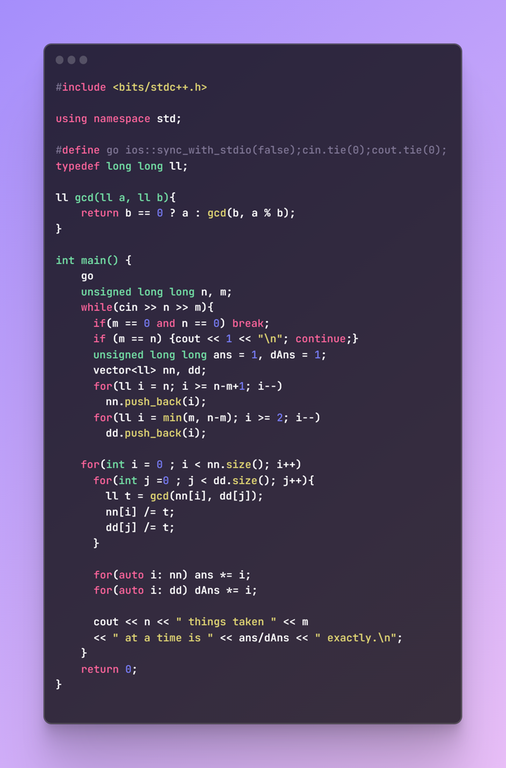

but it gives me WA, I'm not really sure why I'm getting this. Any ideas?

  • Vote: I like it
  • +1
  • Vote: I do not like it

Comments Comments (12)
| Write comment?
»
17 months ago, # |
  Vote: I like it 0 Vote: I do not like it

The problem is to calculate a binomial coefficient.

USACO — How to implement this

Wikipedia — More about binomial coefficients

→ Reply
  • »
    »
    17 months ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Thank you!.
    I've already seen that there are others methods to solve this, however, I want to know what's wrong in my code, I tried to search on YouTube and I saw a guy wrote the same code and had AC

    → Reply
»
17 months ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Two things I noticed:

  1. Why are you using $$$\prod_{i = 1} ^ {min(m, m - n)} i$$$? I'm pretty sure this is what is causing you to get WA. There is no reason to have a min here.
  2. Why have a dAns? You know that the result is integral, and you've already done all the division using the gcd trick. So I think dAns is completely unecessary.
→ Reply
  • »
    »
    17 months ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    For point no.1 you mentioned: for $$$N=100, M=40$$$ for example you want be sure to get rid of the $$$max(M!, (N-M)!)$$$ $$$\frac{100!}{40!\cdot (100-40)!}$$$ you want to cancel $$$60!$$$ to reduce the multiplicated numbers so you divide on the $$$min$$$ between them, in other words you have to divide on one of them and cancel the other, so you choose the $$$max$$$ to be cancelled from the numerator and denominator and divide on the $$$min$$$.
    For point no.2: you need dAns in case there's a number $$$x$$$ in the denominator such that $$$gcd(x,y_i)=1$$$ for $$$0 \leq i\leq nn.size()$$$

    → Reply
    • »
      »
      »
      17 months ago, # ^ |
      ← Rev. 3   Vote: I like it 0 Vote: I do not like it

      For $$$N = 100$$$ and $$$M = 60$$$ you are currently using $$$\prod_{i = N - M + 1} ^ {N} i = \frac{N!}{(N - M)!} = \frac{100!}{40!}$$$ for the numerator. For the denominator you are using $$$\prod_{i = 1} ^ {min(M, N - M)} i = 40!$$$. This is wrong.

      I still dont see any reason to keep dAns. Thinking about it, dAns is always going to be 1.

      → Reply
      • »
        »
        »
        »
        17 months ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Also, you may see the YouTube video in previous commens that wrote the same code and had AC

        → Reply
        • »
          »
          »
          »
          »
          17 months ago, # ^ |
            Vote: I like it +10 Vote: I do not like it

          As I was saying in my original comment, you are erroneously using min for the formula for the numerator. Read through the code in the youtube video again, its calculation for the numerator is different from your code. The youtube code doesn't involve calling min when calculating the numerator.

          My advice is to use a pen and paper, write down the definition for binomial coefficient, and then from that extract the expression for the numerator and denominator. You will see that you don't need to have any mins or maxes anywhere.

          → Reply
»
17 months ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

In the first for loop, replace n-m+1 with n-min(m, n-m)+1.

→ Reply
»
17 months ago, # |
  Vote: I like it 0 Vote: I do not like it

What a text editor do you use ?

→ Reply