Всем привет! Просим прощения за задержку >_<
Надеемся, что вам понравились наши задачи! Извините за то, что лимиты по времени и памяти в некоторых задачах были слишком жесткими и решения на Java не проходили С (кстати, у одного из авторов бывшый ник — "java." :D). Постараемся не допустить таких ошибок вновь.
Оставляйте впечатления и пожелания в комментариях! Спасибо за участие!
1867A — green_gold_dog, массив и перестановка
Автор: green_gold_dog
Из минимального числа вычтем $$$n$$$, из следующего $$$n - 1$$$, из следующего $$$n - 2$$$, $$$\ldots$$$, из максимального $$$1$$$. Тогда количество различных элементов будет $$$n$$$. Очевидно лучшего результа достичь невозможно.
Докажем, что количество различных элементов будет равно $$$n$$$. Допустим $$$c_i = c_j$$$, тогда без ограничения общности скажем, что $$$b_i > b_j$$$, тогда $$$a_i \leq a_j$$$, значит $$$c_i = a_i - b_i$$$ < $$$a_j - b_j = c_j$$$. Противоречие.
Асимптотика: $$$O(n \log n)$$$ на набор входных данных.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
void solve() {
ll n;
cin >> n;
vector<pair<ll, ll>> arr(n);
for (ll i = 0; i < n; i++) {
ll x;
cin >> x;
arr[i].first = x;
arr[i].second = i;
}
vector<ll> ans(n);
sort(arr.begin(), arr.end());
reverse(arr.begin(),arr.end());
for (ll i = 0; i < n; i++) {
ans[arr[i].second] = i + 1;
}
for (auto i : ans) {
cout << i << ' ';
}
cout << '\n';
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
ll t = 1;
cin >> t;
for (ll i = 0; i < t; i++) {
solve();
}
}
Автор: ace5
Во-первых, строка является палиндромом если и только если для любого $$$i$$$ ($$$1 \leq i \leq n$$$) $$$s_i = s_{n-i+1}$$$ (потому что при развороте $$$s_i$$$ становится $$$s_{n-i+1}$$$).
Мы можем разбить символы на пары, где в паре будут $$$s_i$$$ и $$$s_{n-i+1}$$$. Если $$$s_i = s_{n-i+1}$$$, то нам нужно иметь $$$l_i = l_{n-i+1}$$$, чтобы после ксора получились равные элементы. Поэтому либо $$$l_i = l_{n-i+1} = 0$$$ ($$$0$$$ единиц) либо $$$l_i = l_{n-i+1} = 1$$$ ($$$2$$$ единицы). Если же $$$s_i \neq s_{n-i+1}$$$, то должно быть $$$l_i \neq l_{n-i+1}$$$ ($$$1$$$ единица в любом случае). Дополнительно, если $$$n$$$ нечетное, то $$$l_{n/2+1}$$$ может быть либо $$$0$$$, либо $$$1$$$ ($$$0$$$ или $$$1$$$ единица).
Мы можем перебрать, сколько пар где $$$l_i = l_{n-i+1}$$$ будут иметь две единицы а также будет единица по центру или нет, так мы сможем получить все возможные количества единиц в $$$l$$$, то есть все хорошие $$$i$$$.
Асимптотика: $$$O(n)$$$ на набор входных данных.
#include <bits/stdc++.h>
using namespace std;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
int t;
cin >> t;
while(t--)
{
int n;
cin >> n;
string s;
cin >> s;
string t(n+1,'0');
int ans = 0;
int max_1 = 0;
int max_2 = 0;
for(int i = 0;i <= n/2-1;++i)
{
if(s[i] == s[n-i-1])
max_2++;
else
ans++;
}
if(n%2 == 1)
max_1++;
for(int j = 0;j <= max_2;++j)
{
for(int k = 0;k <= max_1;++k)
{
t[ans + j*2 + k] = '1';
}
}
cout << t << "\n";
}
}
Автор: salyg1n
Правильной стратегией за Алису является добавление в множество $$$S$$$ числа $$$\operatorname{MEX}(S)$$$ на первом ходу, и добавление последнего удаленного числа на оставшихся ходах.
Пусть m = $$$\operatorname{MEX}(S \cup {\operatorname{MEX}(S)})$$$, на момент начала игры. Иначе говоря m равняется второму $$$\operatorname{MEX}$$$ множества $$$S$$$. $$$m \geq 1$$$.
Заметим, что после первого хода выполнится $$$\operatorname{MEX}(S) = m$$$, а дальше что бы не удалил Боб, мы вернем это число в множество, а значит результат игры всегда будет равен $$$m$$$.
Докажем, что при оптимальной игре боба мы не сможем получить результат больше m.
Заметим, что $$$\operatorname{MEX}$$$ множества — это наибольшее число k, такое что все числа от $$$0$$$ до $$$k-1$$$ включительно содержатся в этом множестве.
Пусть $$$p_i$$$ равно количеству чисел от $$$0$$$ до $$$i-1$$$ включительно встречающихся в множестве $$$S$$$. Тогда $$$\operatorname{MEX}(S)$$$ равен максимальному $$$i$$$ такому, что $$$p_i = i$$$.
Если Боб во время своего хода удалит число $$$y$$$, он уменьшит на $$$1$$$ все значения $$$p_i$$$, где $$$i > y$$$. Тогда если $$$y = \operatorname{min}(S)$$$, боб уменьшит на $$$1$$$ все ненулевые значения $$$p_i$$$.
Алиса может в свой ход увеличить некоторые значения $$$p_i$$$ на $$$1$$$. Значит после первого хода Алисы, $$$\operatorname{MEX}(S)$$$ уже не будет увеличиваться, если Боб будет удалять минимум, т.к. никакие ненулевые $$$p_i$$$ не будут увеличиваться (Боб их уменьшать на $$$1$$$, а Алиса увеличивать не более чем на $$$1$$$).
Очевидно, что чтобы Алисе максимизировать $$$\operatorname{MEX}(S)$$$ после первого хода, ей необходимо добавить в множество $$$S$$$ число $$$\operatorname{MEX}(S)$$$.
Мы доказали, что $$$R \leq m$$$ и предоставили стратегию которая получает результат $$$m$$$.
Асимптотика: $$$O(n)$$$ на набор входных данных.
#include <iostream>
#include <vector>
using namespace std;
void solve() {
int n;
cin >> n;
vector<int> s(n);
for (int i = 0; i < n; ++i)
cin >> s[i];
int mex = -1;
for (int i = 0; i < n; ++i) {
if (i == 0 && s[i] != 0) {
mex = 0;
break;
}
if (i > 0 && s[i] != s[i - 1] + 1) {
mex = s[i - 1] + 1;
break;
}
}
if (mex == -1)
mex = s[n - 1] + 1;
cout << mex << endl;
int y;
cin >> y;
while (y != -1) {
cout << y << endl;
cin >> y;
}
}
int main() {
int t;
cin >> t;
while (t--)
solve();
return 0;
}
Автор: ace5
Если $$$k = 1$$$ то мы можем менять $$$b_i$$$ на $$$i$$$, поэтому ответ YES только если $$$b_i = i$$$, иначе ответ NO.
Иначе, построим неориентированный граф на $$$n$$$ вершинах с ребрами ($$$i, b_i$$$). Любая компонента этого графа будет выглядеть как цикл(возможно из $$$1$$$ вершины) к каждой вершине которого подвешено дерево(возможно, пустое).
Пусть в компоненте $$$x$$$ вершин, тогда в ней и $$$x$$$ ребер(так как из каждой вершины выходит одно ребро). Мы можем построить дерево обхода dfs этой компоненты, в нем будет $$$x - 1$$$ ребро. Теперь, когда мы добавим оставшееся ребро ($$$u, v$$$), в компоненте образуется один цикл(образованный ребром ($$$u, v$$$) и путем между $$$u$$$ и $$$v$$$ в дереве обхода dfs). К каждой вершине будет подвешено дерево, потому что до добавления ребра у нас было дерево.
Теперь утверждается, что если цикл в каждой компоненте имеет размер ровно $$$k$$$, то ответ YES, а иначе NO.
Для начала рассмотрим ситуацию, где в какой-то компоненте размер цикла не $$$k$$$. Пусть цикл содержит вершины $$$v_1, v_2, \cdots, v_x$$$ в таком порядке. Тогда посмотрим на последнюю операцию, в которой одно из $$$l_i$$$ было равно какому-то элементу из цикла. Если размер цикла меньше $$$k$$$, то в последней операции будет хотя бы одна вершина не из цикла, значит хотя бы одна вершина из цикла заменится на номер вершины не из цикла, что неверно, ведь каждая вершина из цикла должна заменится на номер следующей после нее вершины. Если размер цикла больше $$$k$$$, то у нас будет вершина из цикла, которая заменится не на следующую вершину из цикла(иначе мы бы поиспользовали все вершины цикла, а их больше чем $$$k$$$). Следовательно в любом случае корректной последней операции с вершинами из цикла не существует, поэтому ответ NO.
Если в компоненте размер цикла равен $$$k$$$, то мы можем применить следующий алгоритм:
Пока в компоненте есть хотя бы одна вершина $$$v$$$, которая является листом, мы будем делать операцию с $$$l = [v, b_v, b_{b_v}, \cdots]$$$ (все элементы различны так как мы придем в цикл а он размера $$$k$$$). После этой операции у нас станет $$$a_v = b_v$$$, и мы можем убрать вершину $$$v$$$(из нее шло только $$$1$$$ ребро).
Когда останется только цикл, мы можем применить операцию для вершин цикла, сохраняя порядок, после чего для всех вершин компоненты будет $$$a_v = b_v$$$. Проделав это со всеми компонентами получим $$$a = b$$$, что и требовалось, поэтому ответ YES.
Асимптотика: $$$O(n)$$$ на набор входных данных.
#include <bits/stdc++.h>
using namespace std;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
int t;
cin >> t;
while(t--)
{
int n,k;
cin >> n >> k;
int b[n];
int vis[n];
for(int j = 0;j < n;++j)
{
cin >> b[j];
vis[j] = 0;
}
if(k == 1)
{
int no = 0;
for(int j = 0;j < n;++j)
{
if(b[j] != j+1)
{
no = 1;
}
}
cout << (no ? "NO\n" : "YES\n");
continue;
}
int num[n];
int no = 0;
int tgr = 1;
for(int j = 0;j < n;++j)
{
if(!vis[j])
{
int ind = j;
int cnum = 0;
while(!vis[ind])
{
vis[ind] = tgr;
num[ind] = cnum++;
ind = b[ind]-1;
}
if(vis[ind] != tgr)
{
tgr++;
continue;
}
if(cnum-num[ind] != k)
{
no = 1;
break;
}
tgr++;
}
}
cout << (no ? "NO\n" : "YES\n");
}
}
1867E1-salyg1n и массив (простая версия)
Автор: salyg1n
Сделаем запросы к подотрезкам начинающимся в позициях $$$1$$$, $$$k + 1$$$, $$$2k + 1$$$, $$$\ldots$$$ $$$m \cdot k + 1$$$, пока эти запросы корректны, то есть их правая граница не превосходит $$$n$$$. Сохраним $$$\operatorname{XOR}$$$ всех ответов на эти запросы. Назовем эти запросы первичными.
Теперь будем сдвигать последний подотрезок запроса на единицу вправо и делать новый запрос, пока правая граница не превосходит $$$n$$$. Назовем эти запросы вторичными. Утверждается, что $$$\operatorname{XOR}$$$ всего массива будет равен $$$\operatorname{XOR}$$$'у всех запросов. Докажем это.
Пусть $$$i$$$ "--- позиция в которой начинается первый вторичный запрос. Заметим, что после этого запроса, подотрезок [$i$; $$$i + k - 2$$$] превратится в подотрезок [$$$i + 1$$$; $$$i + k - 1$$$] и развернется. После следующего запроса произойдет то же самое, отрезок сдвинется на единицу вправо и развернется. Значит префиксы длины $$$k-1$$$ каждого вторичного запроса "--- одинаковые, с точностью до разворота, который не влияет на $$$\operatorname{XOR}$$$. Так как количество вторичных запросов равно $$$n \operatorname{mod} k$$$, что является четным числом, $$$\operatorname{XOR}$$$ этих префиксов не будет влиять на $$$\operatorname{XOR}$$$ всех вторичных запросов, который следовательно будет равен $$$\operatorname{XOR}$$$'у элементов [$a_{i + k — 1}$; $a_n$], то есть всех элементов, которых мы не учли в первичных запросах.
Количество первичных запросов равно $$$\lfloor \frac{n}{k} \rfloor \leq k \leq 50$$$, так как. $$$n \leq k^2 \leq 2500$$$.
Количество вторичных запросов равно $$$n \operatorname{mod} k < k <= 50$$$, так как. $$$k^2 \leq 2500$$$.
Итоговое количество запросов не превосходит $$$100$$$.
#include <iostream>
using namespace std;
int ask(int i) {
cout << "? " << i << endl;
int x;
cin >> x;
return x;
}
void solve() {
int n, k;
cin >> n >> k;
int res = 0;
int i;
for (i = 1; i + k - 1 <= n; i += k)
res ^= ask(i);
for (; i <= n; ++i)
res ^= ask(i - k + 1);
cout << "! " << res << endl;
}
int main() {
int t;
cin >> t;
while (t--)
solve();
return 0;
}
1867E2-salyg1n и массив (сложная версия)
Автор: salyg1n
Сделаем запросы к подотрезкам начинающимся в позициях $$$1$$$, $$$k + 1$$$, $$$2k + 1$$$, $$$\ldots$$$ $$$m \cdot k + 1$$$, так, чтобы размер непокрытой части был больше $$$2 \cdot k$$$ и не больше $$$3 \cdot k$$$. Иначе говоря $$$2 \cdot k < n - (m + 1) \cdot k \le 3 \cdot k$$$. Сохраним $$$\operatorname{XOR}$$$ всех ответов на эти запросы. Назовем эти запросы первичными.
Пусть размер оставшейся (непокрытой) части равен $$$x$$$ ($$$2 \cdot k < x \le 3 \cdot k$$$). Научимся решать задачу для массива размера $$$x$$$ за три запроса.
Если $$$x = 3 \cdot k$$$ просто сделаем запросы к позициям $$$1$$$, $$$k + 1$$$, $$$2 \cdot k + 1$$$.
Иначе пусть $$$y = x - k$$$. Заметим, что $$$y$$$ "--- четное, так как $$$x$$$ и $$$k$$$ четные.
Сделаем запросы в позициях $$$1$$$, $$$1 + \frac{y}{2}$$$, $$$1 + y$$$.
Заметим, что после этого запроса, подотрезок [$1$; $$$k - \frac{y}{2}$$$] превратится в подотрезок [$$$y/2 + 1$$$; $$$k$$$] и развернется. После следующего запроса произойдет то же самое, отрезок сдвинется на единицу вправо и развернется. Значит префиксы длины $$$k - \frac{y}{2}$$$ каждого запроса "--- одинаковые, с точностью до разворота, который не влияет на $$$\operatorname{XOR}$$$. Так как количество запросов второй группы равно $$$3$$$, что является нечетным числом, $$$\operatorname{XOR}$$$ этих префиксов учтется ровно один раз в $$$\operatorname{XOR}$$$'е всех запросов, который следовательно будет равен $$$\operatorname{XOR}$$$'у элементов.
Количество первичных запросов не превосходит $$$\lfloor \frac{n}{k} \rfloor \leq k \leq 50$$$, так как. $$$n \leq k^2 \leq 2500$$$.
Итоговое количество запросов не превосходит $$$53$$$.
#include <iostream>
using namespace std;
int ask(int i) {
cout << "? " << i << endl;
int x;
cin >> x;
return x;
}
void solve() {
int n, k;
cin >> n >> k;
int res = 0;
int i;
for (i = 1; n - i + 1 >= 2 * k; i += k)
res ^= ask(i);
if (n - i + 1 == k) {
res ^= ask(i);
cout << "! " << res << endl;
return;
}
int y = (n - i + 1 - k) / 2;
res ^= ask(i);
res ^= ask(i + y);
res ^= ask(i + 2 * y);
cout << "! " << res << endl;
}
int main() {
int t;
cin >> t;
while (t--)
solve();
return 0;
}
1867F-Максимально не похожее дерево
Автор: green_gold_dog
Скажем, что $$$\it{ответ}$$$ для дерева $$$G'$$$ это количество поддеревьев в $$$P(G')$$$ к которым есть изоморфные в $$$P(G)$$$.
Давайте найдём дерево $$$T$$$ минимально размера, к которому нет изоморфного в $$$P(G)$$$. Скажем, что размер дерева $$$T$$$ это $$$x$$$. Тогда возьмём бамбук размера $$$n - x$$$, подвесим $$$T$$$ к последней вершине бамбука и скажем, что это и есть то дерево $$$G'$$$, которое мы искали (корнем $$$G'$$$ будет первая вершина бамбука). Количество совпадающих поддеревьев будет не больше $$$x - 1$$$, т.к. все поддеревья вершин бамбука (к которому мы подвесили $$$T$$$) и само поддерево $$$T$$$ не будут иметь изоморфные в $$$P(G)$$$, ведь в их поддереве есть поддерево $$$T$$$, к которому нет изоморфного в $$$P(G)$$$, значит ответ не более $$$n - (n - x) - 1 = x - 1$$$.
Докажем почему ответ не может быть меньше $$$x - 1$$$: представим, что существует дерево $$$G*$$$ для которого ответ меньше $$$x - 1$$$. Тогда найдём в нём поддерево минимального размера, размер которого не меньше $$$x$$$ (оно всегда найдётся, ведь как минимум можно взять все дерево), в этом поддереве есть еще хотя бы $$$x - 1$$$ поддерево, у каждого из них размер строго меньше $$$x$$$ (ведь на прошлом шаге мы выбрали поддерево минимального размера не меньшего $$$x$$$), а т.к. ко всем деревьям размера меньше $$$x$$$ есть изоморфные в $$$P(G)$$$ (ведь по определению $$$T$$$ — это дерево минимального размера, к которому нет изоморфного в $$$P(G)$$$, а его размер $$$x$$$) то количество совпадающих поддеревьев в дереве $$$G*$$$ это хотя-бы $$$x - 1$$$, противоречие.
Значит в нашем случае ответ $$$x - 1$$$ и меньше быть не может.
Теперь вторая часть задачи — найти $$$T$$$. Для того чтобы это сделать, давайте найдём сначала все деревья размера 1, потом 2, потом 3, 4, и так далее пока не найдем дерево, которому нет изоморфных в $$$P(G)$$$. Можно заметить, что если сгенерировать все деревья размера не больше 15, то там точно найдется $$$T$$$. Внутри каждого размера пронумеруем деревья в порядке перебора. Для того, чтобы найти все деревья размера $$$x$$$ имея все деревья размера $$$x - 1$$$ или меньше давайте скажем, что размеры детей у корня дерева, которое мы генерируем, должны не убывать, а если размеры совпадают, то номера должны не убывать, тогда можно перебрать первого сына, потом среди меньших и подходящих по размеру второго, потом третьего, и так далее пока размер нашего дерева не станет ровно $$$x$$$, тогда мы переберём все деревья размера $$$x$$$ за их количество (т.к. мы не рассмотрим ни одно дерево дважды и лишних тоже не рассмотрим). Будем это делать пока не найдем дерево, которого нет в $$$P(G)$$$.
Для сравнения деревьев на изоморфность можно использовать хеши. Подробнее прочитайте в блоге:
Асимптотика: $$$O(n \log n)$$$.
#include <bits/stdc++.h>
using namespace std;
const int MAXSZ = 15;
void rec(int ns, int last, vector<int>& now, vector<vector<int>>& aint, vector<int>& col, vector<int>& sz, int& ss, int sns) {
if (ss < 0) {
return;
}
if (ns == 0) {
col.back()++;
aint.push_back(now);
ss -= sns;
return;
}
for (int i = min(last, col[ns] - 1); i >= 0; i--) {
now.push_back(i);
rec(ns - sz[i], i, now, aint, col, sz, ss, sns);
now.pop_back();
}
}
void dfs(int v, int p, vector<vector<int>>& arr, vector<int>& num, map<vector<int>, int>& m, vector<int>& sz) {
vector<int> now;
sz[v] = 1;
for (auto i : arr[v]) {
if (i != p) {
dfs(i, v, arr, num, m, sz);
sz[v] += sz[i];
if (sz[v] <= MAXSZ) {
now.push_back(num[i]);
}
}
}
if (sz[v] > MAXSZ) {
num[v] = -1;
return;
}
stable_sort(now.begin(), now.end());
reverse(now.begin(), now.end());
num[v] = m[now] - 1;
}
void dfs2(int x, int p, vector<vector<int>>& aint, vector<int>& ans) {
if (p >= 0) {
ans.push_back(p);
}
int now = ans.size();
for (auto i : aint[x]) {
dfs2(i, now, aint, ans);
}
}
void solve() {
int n;
cin >> n;
vector<vector<int>> aint(1);
vector<vector<int>> arr(n);
for (int i = 1; i < n; i++) {
int a, b;
cin >> a >> b;
a--;
b--;
arr[a].push_back(b);
arr[b].push_back(a);
}
map<vector<int>, int> m;
vector<int> col(1, 0), sz(1, 1);
col.push_back(1);
for (int i = 2; i <= MAXSZ; i++) {
vector<int> now;
col.push_back(col.back());
int ss = n;
rec(i - 1, aint.size() - 1, now, aint, col, sz, ss, i);
while (sz.size() < col.back()) {
sz.push_back(i);
}
if (ss < 0) {
break;
}
}
for (int i = 0; i < col.back(); i++) {
m[aint[i]] = i + 1;
}
vector<int> num(n), szi(n, 1);
dfs(0, 0, arr, num, m, szi);
set<int> s;
for (int i = 0; i < col.back(); i++) {
s.insert(i);
}
for (auto i : num) {
s.erase(i);
}
int x = *s.begin();
vector<int> ans;
if (sz[x] > n) {
for (int i = 0; i < n; i++) {
for (auto j : arr[i]) {
if (i < j) {
cout << i + 1 << ' ' << j + 1 << '\n';
}
}
}
return;
}
for (int i = 0; i < n - sz[x] - 1; i++) {
ans.push_back(i);
}
dfs2(x, n - sz[x] - 1, aint, ans);
for (int i = 0; i < ans.size(); i++) {
cout << ans[i] + 1 << ' ' << i + 2 << '\n';
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t = 1;
//cin >> t;
for (int i = 0; i < t; i++) {
solve();
}
}










If you were wondering why am I an author but didn't make any problems: a day before the contest we decided to replace my task F (because I hate it) and to give "Most Different Tree" instead, hopefully it fits better (I guess we'll never know) :]
Video Editorial for A-E2 ...I hope it will helpful to Newbies and Pupils..! YOUTUBE EDITORIAL LINK
In 1867E2 - Salyg1n and Array (hard version) it is impossible to achieve $$$2k < x$$$ if $$$n \leq 2k$$$. However, in fact we do not need this condition. The second part of the solution still works in the case $$$k < x \leq 2k$$$.
E2 can be actually done in 51 operations instead of 57.
When k divides n then it only takes n/k queries, i.e 50 at max.
Otherwise, we can separate the first n*[n/k] elements and the remaining n%k elements. Since, n%k is even then we can divide those remaining elements in 2 parts of (n%k)/2 size. First, we ask a query where the i+k-1=n-(n%k)/2. Then after the subarray gets reversed, we again ask another query where i+k-1=n. Taking XOR of their outputs, the common elements gets nullified and we get our requried value.
This takes [n/k]+2=49+2=51 queries.
Submission E2
Nice solution!
Here's a sort of visual proof of why this works: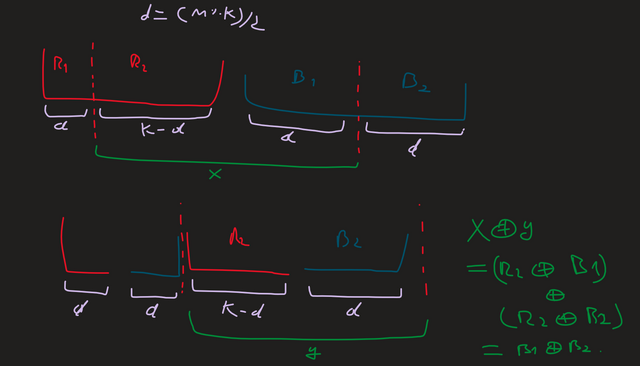
Yeah, we know, our solution does 51 queries too. Number 57 is just cool. Also the limit of 51 quiries could be a hint
Nice! Easy to understand!
lol
Disclaimer: I'm a stupid newbie code Note: Yet plz continue reading Many accepted solutions, including this official editorial solution, are giving answers other than the correct answer (1) for the following test case:
t=1 n=9 k=4 array = [1, 2, 3, 4, 5, 6, 7, 8, 9]The problem statement mentions both n and k will be even
Yeah, you just answered your own question.
Thank you for editorial <3
runtime error @testcase3 for D, grateful if someone can find the error ! fk this shit mann!
Python has a default maximum recursion depth of 1000. Since n is of the order 2e5, it is not possible to do it in a recursive fashion. Try writing your dfs using stacks or just use while loops.
Note that you may also try increasing the recursion depth limit ( sys.setrecursionlimit(N) ) but that would just lead to MLE.
what's MLE
Memory limit exceeded
E1 and E2 was possible to make more interesting by pushing a condition when (k+n)%2==0 ,worst case it would take more two moves than optimal solution.
It was possible to make problem E1 and E2 more interesting by pushing extra condition (n+k)%2==0.
In the problem 1867E2 — Salyg1n and Array (hard version) for a case where n = 3, k = 2 and a = [4, 2, 5] the answer should be 3. But the given solution in the editorial is providing the answer 6. The interaction is given below,
Can someone explain the case?
Read problem statement clearly , here n and k always even. And the information you got ,is not enough.
Thank you. I should have been more careful.
Can someone please explain why was this submission skipped https://codeforces.net/contest/1867/submission/222952890 ? It have gotten AC on pretests and i also sent almost identical one (added pragmas) later and it got AC.
Because later you submitted another submission and it also passed pretests. Only your last AC submission is tested on sistests
वीडियो स्पष्टीकरण A,B,C,D
bhaiya i watched the video but not able to get the B what should i do
I was too lazy to code some general tree enumeration for F, so I got a slightly different solution.
Expand a little on the jury's observations. The answer always (except for $$$n=2$$$) looks like that: some tree that is not in $$$P(G)$$$, all its children are in $$$P(G)$$$ and there's a long bamboo attached to its root. The value of the answer is the sum of the sizes of the children.
Now, recall the hashing part of the isomorphism check procedure. We take the isomorphism classes of all children of a vertex, sort them and get the class of the whole tree based on that list. Imagine building the answer with that procedure. The resulting list should not appear among the existing classes. However, during the procedure, all prefixes of the list have to appear among them. Otherwise, we could've taken that prefix as the answer.
Thus, the answer looks like that: an existing subtree with another existing subtree attached to it as the last child. Additionally, the class of the last child should be not less than the class of the last child of the initial subtree.
So the solution could look like that. Iterate over the existing classes as the initial tree, then iterate over them again as the last child. If the last child is smaller than the last element of the initial list, skip it. If the list with the new element appended appears among the existing classes, skip it. Find the smallest tree among everything that's left.
Unfortunately, it's too slow as is. Let's optimize.
The second condition is easy to circumvent. Find all existing lists that are the current one with one element appended. You can think of it as building a trie of these lists, then traversing it. Now, you can remove them from some structure of options, then find the best option, then add them back. That would be $$$O(n)$$$ removals and additions in total.
The first condition is harder. I chose to abuse the fact the answer is really small. For each size, store the indices of the classes of all existing trees of that size in the increasing order. Now, we can iterate over the size of the option tree, then lower_bound for the index that is at least as large as the last element of the current list. If the iterator isn't at the end, update the answer and break. If you use a set for that, you can easily support the removals and additions as well.
I believe, that is $$$O(n \cdot \mathit{ans} \cdot \log n)$$$. The submission is 222999827 if anyone is curious.
Can someone please explain why in the A problem I cannot use a multimap?
I think you mixed up the position of the first element of the sorted array in the original array with the position of the first element of the original array in the sorted array.
Do anyone know 42th subtest of test 2 of problem D. I can not pass this anyway
In the editorial of F it is said that "One can see that if we generate all trees of size up to 15 we will definitely find T there."
How do you prove that we only need trees with a size no more than 15?
Because the number of rooted trees of size 15 is more than $$$87000$$$. $$$87000 \cdot 15 > 10^6$$$, so the initial tree can't have all these trees as subtrees. Here's the sequence
ace5, can you please tell me for the problem 1867D - Cyclic Operations what is the motivation for converting this problem into graph . Its just something outside of my thought process that this problem can also be thought like this. So how we actually know of converting it. Is it by just applying other concepts and then checking if they are not working then try another some new concept.
Because i have been thinking like that for the answer to be YES , all the elements in the array must have been permutation of the positions and then are overlapped in a unique fashion and if this condition does not hold somewhere in between then the answer will be NO. But i do not know how we will implement it and just went blank after that.
Can you please explain it will be so kind of you as i have spent a significant amount of time but still have no idea.
.
A much more sane way to implement F is to recognize that you can enumerate all RBS of length 28 to cover the euler tour of every tree of size 15 (with repetitions); there are 2.6e6 of them which barely fits in the TL. However, you can also use this method for sizes up to 14 and just use random to solve size 15 (less than 80% of size 15 trees can be subtrees), which should reduce the runtime by a factor of 3.6 and comfortably pass.
https://codeforces.net/contest/1867/submission/223380152
I want to ask In problem E: how come this sample is accepted n=3 k=2 and the array is 1 2 4 the judges code is answering 6 when in fact it should be 7 but there is no definite way to know the answer.
Notice that problem statement states n and k are even numbers. It can be shown that this ensures uniqueness of the answer.
In E1/E2, if anyone is wondering if solution for any cases where n & k are not both even is possible or not. I tried some examples and found out that I can construct a solution if k is odd (doesn't matter whether n is odd or even). But when k is even we can prove that solution is not possible if n is odd.
Initially, we can only get xor of even subarray sizes. Now, let's say there are 2 sets of even size (say x & y). And t elements are common in these 2 sets, after taking xor of these 2 sets we again get new set of even size i.e. x + y — 2t. So, constructing a set of odd size i.e. n is not possible when k is even.
Note: Can someone please confirm my claim or prove me wrong?
For problem F, I can't understand why I got wa for this code. Who can help me find out the problem please qwq. https://mirror.codeforces.com/contest/1867/submission/223794337
Hi everyone its really hard for me to understand problem D. I have watched many videos and editorial but not able to understand problem D . Can anyone tell me what should I do?
So, the idea is first to understand how the operation works. You can try some examples with 1 2 3 4 and play with it(reverse order of them). You will realise: you cant get a number on its index(1 cant stay on first index, 2 on second...), and you must go in cycle to come back to 1(if you set first index to 3, index 3 must be 2 or 4 lets say 4, index 4 can be only 2 and index 2 1). After that try to do example: k = 4, array = 2 3 4 1 1, you will understand that you can do 1 operation to get 1 on fifth index and after that do operation on first 4 to solve them. So the conclusion is: if you have a good cycle of 4(cycle where all numbers remain in their indexes:3 5 4 5 1 5 5 5 example where indexes 1 3 4 5 are a good cycle, you can first solve for all other indexes that have one of those 4 numbers and then solve the cycle), but if you have a cycle of 3 when k is equal 4 you cant solve the problem(you can make only 4 cycle rotations). So the problem becomes finding good cycle indexes and all other indexes that have good cycle indexes as value and hoping that after finding all of those whole array is done. So we need to find cycles between numbers and their connections to rest of the array which is nothing more than a graph.
why hacks in third problem are forbidden?
Can some one explain in problem D, what is the insight that leads to constructing a directed graph with edges going from i to b[i] ? Specifically, why use edges from i to b[i] ?
for(int j = 0;j <= max_2;++j) { for(int k = 0;k <= max_1;++k) { t[ans + j*2 + k] = '1'; } } in B can you explain this part
Зашло вот такое решение:
pragma GCC optimize("O3,unroll-loops")
pragma GCC target("avx2,bmi,bmi2,lzcnt,popcnt")
include <bits/stdc++.h>
using namespace std;
define int long long
define endl "\n"
int n; vector<vector> vec; map<vector,int> tree; vector sz;
int f(vector &a){ if(tree.count(a)){ return tree[a]; } int v=tree.size(); vec.push_back(a); int s=1; for(auto x : a){ s+=sz[x]; } sz.push_back(s); return tree[a]=v; }
signed main() { ios::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL); cin >> n; vector<vector> adj(n); for(int i=0;i<n-1;i++){ int u,v;cin>>u>>v; u--,v--; adj[u].push_back(v); adj[v].push_back(u); } if(n==2){ cout<<1<<" "<<2<<endl; return 0; } set se; auto dfs=[&](auto &&dfs,int u,int fa)->int{ vector a; for(auto v : adj[u]){ if(v==fa) continue; a.push_back(dfs(dfs,v,u)); } sort(a.begin(),a.end()); se.insert(f(a)); return f(a); }; dfs(dfs,0,-1); vector a; for(int i=1;i<=n;i++){ vector b,c; auto dfs=[&](auto &&dfs,int sum,int lst)->void{ if(sum==0){ int ret=f(b); if(!se.count(ret)){ int idx=n-i; auto work=[&](auto &&work,int cur)->int{ int now=++idx; for(auto v : vec[cur]){ int val=work(work,v); cout<<now<<" "<<val<<endl; } return now; }; for(int j=1;j<=n-i;j++){ cout<<j<<" "<<j+1<<endl; } work(work,ret); exit(0); } c.push_back(ret); }else{ for(int j=lst;j<a.size();j++){ if(sum>=sz[a[j]]){ b.push_back(a[j]); dfs(dfs,sum-sz[a[j]],j); b.pop_back(); } } } }; dfs(dfs,i-1,0); a.insert(a.begin(),c.begin(),c.end()); sort(a.begin(), a.end()); } }