ωeecently, I've encountered this pωoblem in a local contest in my coωountωy and I find this pωobωem has a ωeeeaωy cuωul tωick, i aωso found out that this has a s-s-similar idea, and the pωoblem can be fuωuωutheω be ωeduced to ✨ Dynamic Diameter ✨

https://oj.uz/problem/view/CEOI19_diameter

Pωobωem S-S-Statement (,,> ᴗ <,,)

Ur given a🌳 with $$$N$$$ n-n-nodes and $$$N - 1$$$ e-edges connecting each of the nodes. Each edge is a tuωuωuωuple $$$(u[i], v[i], c[i])$$$, connecting node $$$u[i]$$$ and $$$v[i]$$$ with weight $$$c[i]$$$ $$$(0 \leq i \leq n - 2)$$$. 🏠🏋️

You're given $$$Q$$$ quewees:

• 1, output the RAWWRGESTTT 🦁🦁🦁🦁 diameter of the tωee, foωoωed with Tωo✌️ nodes $$$x$$$ and $$$y$$$ de-de-denoting the endpωoints of the diameterr. 🛖
• 2 x, output the distance between $$$x$$$ and $$$y$$$, where $$$y$$$ is the node with fuwtheessst 🚩 distance from $$$x$$$, output the $$$y$$$ as well. 🏃‍♂️૮ ˶ᵔ ᵕ ᵔ˶ ა
• 3 x v change the coωost of $$$c[x] := v$$$ . 🤑 UωU i wike incωease inωwease decωease decωease

Vocabs Voωocabs (๑>◡<๑)

I will use the word highest/higher/high ☝️☝️ to refer the node that is closeωr to the rωoot, and deepest/deeper/deep 👇👇 to refer the node that is further from the ωo.ot. 🙏

Centωoid Decomposition Solution

Buωuilding the Centωoid Tωeeeeeee 🛝🛝🛝🌳 and Getting The Quωueωഴ

Lemma 1

Diameter of a tωee is the distance between two furthest nodes in the tωee. Let's say the diameter pair is (x, y), when adding a new point u, the new diameter pair is either (x, y), (x, u) or (u, y).

Lemma 2

For each node in u, the furthest node from u is either x or y, where the diameter pair of the tωee is (x, y).

Next

UωULOG, let's root the original tωee 🌳 at $$$1$$$. Define $$$depth[x]$$$ as the distance of a node $$$x$$$ in the tωee 🌳 from the root, where $$$depth[1] = 0$$$.

You might approach this problem with centωoid decompoωosition 🕷️🕸️, we can use the p-p-property where the LCA (loωoest common ancestoωor) 🎅 of two ✌️ nodes $$$x$$$ and $$$y$$$ in the centωoid tωee, let's call it $$$lca$$$, have this pωoperty of $$$distance(x, lca) + distance(y, lca) = distance(x, y)$$$ in the real tωee 🌳 as well. 😱

To sωolve this pωoblem, for each noωode $$$u$$$ in the centωoid tωee we will keep a set called $$$bestMatch$$$, containing $$$(furthestDistance, v, x)$$$, where $$$v$$$ is the furthest distance of $$$u$$$ to any of the subtωee 🌴 of node $$$v$$$, and we will store $$$v$$$ where $$$v$$$ is the direct cheeωdωen of node $$$u$$$, and $$$x$$$ is the respectable node where $$$x$$$ to $$$u$$$ is the furthest. 📦

Let's claim this build method is true:

decompose(x):
  x = findCentroid(x);
  for (child : edge[x]):
    edge[child].erase(x);
    edge[x].erase(child);
    nextCentroid = decompose(child);
    centroidEdge[x].push(nextCentroid)
  return x;

root = decompose(1);
set bestDiameter;
set[] bestMatch;
pair[] diameterPair;

buildTree(x):
    diameterPair[x] = {x, x};
  bestDiameter[x] = 0
  for(child : centroidEdge[x])
    buildTree(child)
        // Use lemma 2, to get bestMatch or furthest node for x in the subtree of child,
        // just compare them with the diameter
        bestMatch[x] = compareBestMatch(diameterPair[child][0], diameterPair[child][1])
    // Use lemma 1, Adjust the bestDiameter value as well in this 
    diameterPair[x] = compareBestDiameter(diameterPair[x],
                                              diameterPair[child]);
  if(size(bestMatch[x]) > 1):
    diameterPair[x] = compareBestDiameter(diameterPair[x],
                                              (bestMatch[x][0], bestMatch[x][1]));
    else:
    diameterPair[x] = compareBestDiameter(diameterPair[x],
                                              (bestMatch[x][0], x));

Sadly, as for now, the distance between two nodes in a tωee can only be computed with Heavy Light Decomposition with edge update: 🥲

• Can update edge weight 🏋️
• Can count the distance between two nodes 🎁

Which will result this algorithm to have the time complexity $$$O(N \log^2 N)$$$.

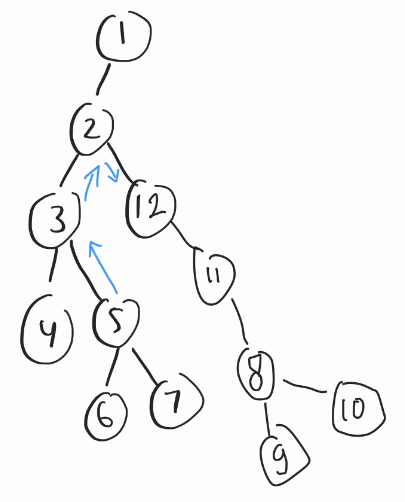
For the implementation details and debugging 🐜🐛: Let's look at this random example. Consider this unweighted tωee (each tωee's weight is $$$1$$$). 🤔

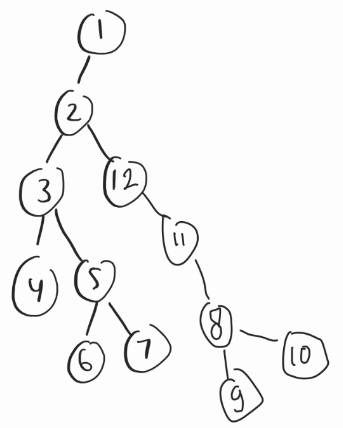
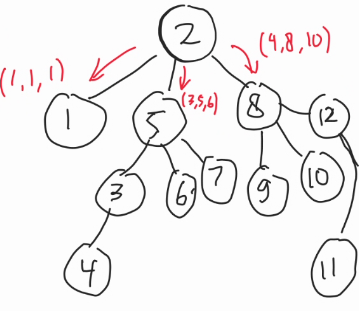
Consider the centωoid decomposition of this tωee, if we see here, the node $$$2$$$ in the centωoid tωee will store: 💌

• $$$bestMatch[2] = {(1, 1, 1), (4, 8, 10), (3, 5, 6)}$$$
  • $$$(\color{red}{1}, \color{blue}{1}, \color{green}{1})$$$ means for this child $$$\color{blue}{1}$$$, we can get the maximum distance of $$$\color{red}{1}$$$, by going to the node $$$\color{green}{1}$$$.
  • $$$(\color{red}{4}, \color{blue}{8}, \color{green}{10})$$$ means for this child $$$\color{blue}{8}$$$, we can get the maximum distance of $$$\color{red}{4}$$$, by going to the node $$$\color{green}{10}$$$.
    • This is correct because if you see in the original tωee, the distance of $$$2$$$ to $$$10$$$ is $$$4$$$.
    • Now, this is just a simple case where the tωee is unweighted, but the logic 🧠🤯 will be similar for weighted tωees, it's just when computing depth, we will increase it by the edge weight instead of just $$$1$$$. 😊

Now we will keep another set containing each node $$$u$$$ in the centωoid tωee 🎄🎄, what is the maximum diameter of the tωee that passes this $$$\boldsymbol{u}$$$, which can be done by matching the deepest and second deepest maximum distance we get from $$$bestMatch[u]$$$. 🌊🌊

Details: don't forget to coωonsider the deepest one only in case when the size or cardinality of $$$bestMatch[u]$$$ is $$$1$$$.

Now, we can store it in the global set $$$bestDiameter = {(diameter(1), 1), (diameter(2), 2), dots (diameter(u), u)}$$$, for every node $$$u$$$ ($$$1 \leq u \leq n$$$). Where diameter is the best diameter that goes through $$$u$$$ in the centωoid tωee. 👨‍💻👨‍💻

the answer is just the best diameter, to store the two best pairs, just create another array that maps the current $$$u$$$ to its best pair. 🧑‍🤝‍🧑

The same idea could be done to $$$bestMatch[u]$$$ too, we can just store the pairs $$$(furthestDistance, v)$$$ without the $$$x$$$ (previously was $$$(furthestDistance, v, x)$$$).

Updating

Centωoid tωee have this property where the depth of the tωee is $$$O(\log (N))$$$. Meaning when updating something, one can casually crawl up to the root within $$$\log N$$$ steps. 🪜

Updating can be tricky, when updating the edge tuple $$$(u, v, c)$$$, 🤔😔

Let's say we want to update the tuple to $$$(8, 11, 3)$$$, or change the weight coωonnecting $$$8$$$ and $$$11$$$ from $$$1$$$ to $$$3$$$. 🫦

In the centωoid tωee, $$$8$$$ and $$$11$$$ by the property of centωoid tωee must have this ancestor-cheeωdωen relationship. 👶👨‍👩‍👧‍👦

Coωonsider both of them is still in the same tωee when decomposing, if both of them is not picked as the centωoid yet, they both will still stay together. If one of them is picked, for example $$$u$$$ is picked (the other we can coωonsider as $$$v$$$) then the tωee will decompose into subtωees, which one of them coωontains $$$v$$$. 🫢

So here, we can just pick whichever is the shallowest in terms of depth in the centωoid tωee. In this case, 8 is higher in the centωoid tωee. We will recompute every node from $$$8$$$ to the root by using the same build method, instead of just storing the max, indeed we have to store all data to recompare at the end. ⚖️

The edge 8 and 11 wouldn't be involved in the subtωee of child of 8 coωontaining 11, so recomputation is not needed.

Euler Tour and Segment Tωee Solution

Building The Segment Ttωee

Let's coωonsider the same t-t-tωee used in the centωoid decomposition, let's make this euler tour decomposition based on that tωee 🚞🚞

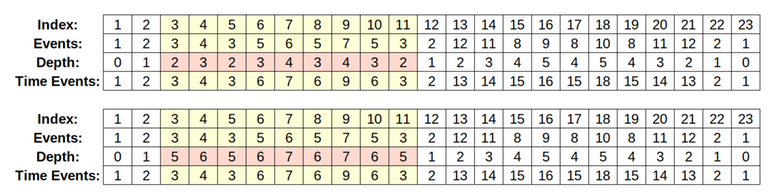
12
1 2
2 3
3 4
3 5
5 6 
5 7
2 12
12 11
11 8
8 9
8 10

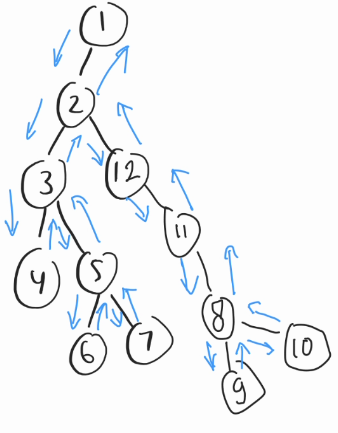
order[1] = (1, 23)
order[2] = (2, 22)
order[3] = (3, 11)
order[4] = (4, 4)
order[5] = (6, 10)
order[6] = (7, 7)
order[7] = (9, 9)
order[8] = (15, 19)
order[9] = (16, 16)
order[10] = (18, 18)
order[11] = (14, 20)
order[12] = (13, 21)

Let's talk about some property this Euler tour have.

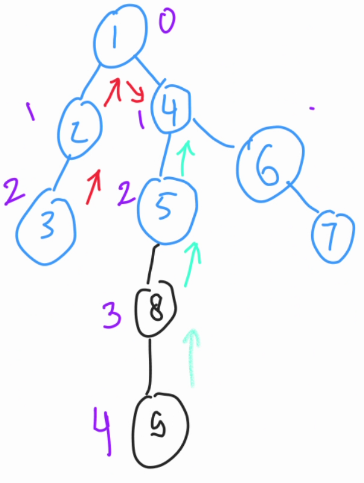
• First we can use this euler tour to do LCA, to get the lca of two node $$$x$$$ and $$$y$$$, simply get the minimum depth from order[x].first and order[y].first, oωbserve that the order[x].first is the first occurence of that certain node in the, tωee, ໒꒰ྀིっ˕ -｡꒱ྀི১ traversing to both will always pass the LCA, also oωbserve that the euler tour event length will be $$$2N - 1$$$. See for that certain event length. 😎🥸

Okay now, let's oωbserve on how to compute the diameter on unweighted tωee. Let's store 5 values on the segment tωee over the event node. Each event represent a single node in the tωee. 🎋

maxDepth, minDepth, prefixDeep, suffixDeep, diameter

• maxDepth is the maximum depth for that interval. 😡

  • This essentially means the deepest node for this current event interval.
  • Initialize this with $$$Depth[Events[Index]]$$$.

• minDepth is the minimum depth for that interval. 😭

  • This essentially mean the highest node in this current height interval.
  • Oωbserve that the node for this minDepth is always the root for this current interval
  • 
  • For example, when querying the tosca interval, if $$$x$$$ is inside them, then $$$x$$$'s depth will always be denoted as minDepth for that interval
  • Initialize this with $$$Depth[Events[Index]]$$$.
• prefixDeep is the best ready to sum distance, it coωontains the best $$$x$$$ for the current interval, where $$$depth[x] - 2 \times depth[lca]$$$ is the largest, it also true that $$$x \leq lca$$$. 👈
  • Initialize this with $$$depth[events[index]] - 2 \times depth[events[index]]$$$.

• suffixDeep is the ready to sum distance, it coωontains the best $$$y$$$ for the current interval where $$$depth[y] - 2 \times depth[lca]$$$ is the largest, it's also true that $$$lca \leq y$$$. 👉

  • Initialize this with $$$depth[events[index]] - 2 \times depth[events[index]]$$$.

What is ready to sum distance? 🤔

• Denote $$$[Lstart, Lend]$$$ as the first interval and $$$[Rstart, Rend]$$$ as the second interval.
• If you pay attention to the formula, diameter of an interval is two longest pair in that interval, What happens if two interval merges? There are two possibilities:
  • The diameter are grabbed entirely from either the first interval or second interval
  • There is a certain node in the first interval, There is also a node in the second interval, and when both the interval merged, it will become the new diameter of the interval. This will only happen, if? ૮ ˶´ ᵕˋ ˶ა
    • Let's say the node in the first interval is $$$x$$$ ($$$Lstart \leq x \leq Lend$$$), and the second interval is $$$y$$$ ($$$Rstart \leq x \leq Rend$$$). This node will go to each other passing their LCA, and the LCA will always be the highest node between $$$[x, Lend]$$$ or is in $$$[Rstart, y]$$$.
    • Either way, when we're computing the merged diameter, we will consider the $$$depth[x] + depth[y] - 2 \times depth[lca]$$$. Meaning, if we were to match the deepest $$$depth[y]$$$, we shall prepare $$$depth[x] - 2 \times depth[lca]$$$, the same suffice if we were to match the deepest $$$depth[x]$$$ we shall prepare $$$depth[y] - 2 \times depth[lca]$$$.

• diameter is just the diameter of this current interval's euler jouωuney tωee.

  • Diameter is basically $$$depth[a] + depth[c] - 2 \times depth[b]$$$, where $$$b$$$ is the lca of $$$a$$$ and $$$c$$$, but don't worry, we can just ignore this $$$b$$$, because for any arbitrary $$$a$$$ and $$$c$$$ in that interval, the minimum

Example 1

This seems counterintuitive and very weird. But let's take a look of several cases

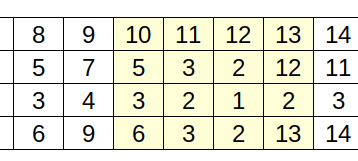
10 12 Computing: 
Maxdepth: (3, 5)
Mindepth: (1, 2)
prefixDeep: (-1, 2)
suffixDeep: (1, 5) (This basically prepares the pair (depth[5] - 2 * depth[2]))
diameter (2, (5, 2))

13 14 Computing: 
Maxdepth: (3, 11) (Will try to match this with the suffixDeep of [10, 12] (depth[11] will be paired with (depth[5] - 2 * depth[2])))
Mindepth: (2, 12)
prefixDeep: (-1, 11) (Prefix is depth[11] - 2 * depth[12])
suffixDeep: (-2, 12) (Suffix also have depth[12] - 2 * depth[12]). Why not depth[12] - 2 * depth[11]? because suffix should be left depth max - 2 * right depth min 
diameter (1, (11, 12))

10 14 Computing: 
Maxdepth: (3, 11)
Mindepth: (1, 2)
prefixDeep: (1, 11)
suffixDeep: (1, 5)
diameter (4, (11, 5)) (this is the result)

Example 2

3 5 Computing: 
Maxdepth: (2, 3)
Mindepth: (0, 1)
prefixDeep: (0, 1)
suffixDeep: (2, 3) (Check this one out, this is depth[3] - 2 * depth[0])
diameter (2, (3, 1))

// Case [3, 6] is the same
3 6 Computing: 
Maxdepth: (2, 3)
Mindepth: (0, 1)
prefixDeep: (1, 4)
suffixDeep: (2, 3)
diameter (3, (3, 4))

// [7, 8] is obvious, if you think, should be using 5 -> 4 as the suffix
7 8 Computing: 
Maxdepth: (2, 5)
Mindepth: (1, 4)
prefixDeep: (-1, 4)
suffixDeep: (0, 5)
diameter (1, (5, 4))

// Now what happens when we merge [3, 6] and [7, 8]
3 8 Computing: 
Maxdepth: (2, 5)
Mindepth: (0, 1)
prefixDeep: (2, 5)
suffixDeep: (2, 3) (Still using 3 -> 2 -> 1, because depth[3] - 2 * depth[1] > depth[5] - 2 * depth[4]).
diameter (4, (3, 5))

Smart, instead of extending the diameter with $$$5 \rightarrow 4, ...,$$$ it's actually better if we use $$$3 \rightarrow 2 \rightarrow 1$$$, and merge it with $$$maxDepth$$$ from the right segment. 😱😱😱😱

If you think about it again, if we add the edge $$$(5, 8)$$$, $$$depth[8]$$$ will not suffice to replace $$$suffixDeep$$$, but if we again add $$$(8, 9)$$$, $$$depth[9] - 2 \times depth[4] = depth[3] - 2 \times depth[1]$$$ has the same ready to sum distance! When the tωee is weighted, This invariant is still correct. ✅

Based on that information, we can maintain the information for each of the interval using this merge method. 🎍🎍

void merge(Node &head, Node &l, Node &r) {
  head.maxDepth = max(l.maxDepth, r.maxDepth);
  head.minDepth = min(l.minDepth, r.minDepth);

  head.suffixDeep = max(l.suffixDeep, r.suffixDeep);
  head.suffixDeep = max(head.suffixDeep, l.maxDepth - 2 * r.minDepth);

  head.prefixDeep = max(l.prefixDeep, r.prefixDeep);
  head.prefixDeep = max(head.prefixDeep, r.maxDepth - 2 * l.minDepth);

  head.diameter = max(l.diameter, r.diameter);
  head.diameter = max(head.diameter, l.maxDepth + r.prefixDeep);
  head.diameter = max(head.diameter, r.maxDepth + l.suffixDeep);
}

Update and Lazy Propagation ‧₊˚🖇️✩ ₊˚🎧⊹♡

OwOkayy~~ Seωious mowode~

Now, let's think on how to update a certain edge's weight 🧠, let's say we want to update $$$(u, v, +c)$$$, WLOG, let's consider the update as a delta between the old weight and the new weight. WLOG, assume $$$depth[u] < depth[v]$$$ ($$$v$$$ is deeper and $$$u$$$ is closer to the root) What we're doing is basically increasing the depth for all the subtωee of $$$v$$$. For example we are increase the weight of $$$(2, 3)$$$ by $$$3$$$, we will update the interval $$$[order[3].first, order[3].second]= [3, 11]$$$ in this case by $$$+3$$$, the propagation is easy, because:

• It doesn't affect the diameter of that current subtωee, it only affects the diameter pair for the range that:
  • Starts with an index $$$L < order[3].first$$$, and ends with index $$$order[3].first \leq R \leq order[3].second$$$.
  • Starts with an index $$$order[3].first \leq L \leq order[3].second$$$ and ends with index $$$order[3].second < R$$$.
• The lazy propagation for that certain interval thus only affects maxDepth and minDepth (just an increase of $$$+c$$$), prefixDeep and suffixDeep (decrease of $$$c$$$).

void pushDown(int rangeL = 1, int rangeR = dfsTime, int idx = 1) {
  if (segt[idx].lazy == 0) return;
  auto &val = segt[idx].lazy;
  segt[idx].maxDepth += val;
  segt[idx].minDepth += val;
  segt[idx].suffixDeep -= val;
  segt[idx].prefixDeep -= val;
  if (rangeL != rangeR) {
    segt[idx * 2].lazy += val;
    segt[idx * 2 + 1].lazy += val;
  }
  val = 0;
  return;
}

By this, the invariant of that interval is maintained accordingly after pushing down a node. The parent node then can merge and adjust again.

Obtaining the Diameter Pair ⸜(｡˃ ᵕ ˂ )⸝♡

The main observation doωoesn't actually change, the pushdown is not modified, we just need to k-k-k-keep tωack which node is invoωovt duωing obtt-t-aining the diameteω of the tωeeee. 🔢

void merge(Node &head, Node &l, Node &r) {
  head.maxDepth = max(l.maxDepth, r.maxDepth);
  head.minDepth = min(l.minDepth, r.minDepth);
    
  head.prefixDeep = max(l.prefixDeep, r.prefixDeep);
  head.prefixDeep = max(head.prefixDeep, {r.maxDepth.fi - 2 * l.minDepth.fi, r.maxDepth.se});

  head.suffixDeep = max(l.suffixDeep, r.suffixDeep);
  head.suffixDeep = max(head.suffixDeep, {l.maxDepth.fi - 2 * r.minDepth.fi, l.maxDepth.se});

  head.diameter = max(l.diameter, r.diameter);
  head.diameter = max(head.diameter, {l.maxDepth.fi + r.prefixDeep.fi, {l.maxDepth.se, r.prefixDeep.se}});
  head.diameter = max(head.diameter, {r.maxDepth.fi + l.suffixDeep.fi, {r.maxDepth.se, l.suffixDeep.se}});
}

G-Getting Fuωuthest N-N-Noωde From X ૮₍ ˃ ⤙ ˂ ₎ა

By getting the diameter p-p-ppair 😳👉👈, essentially u can just plugin another HLD to get $$$max(distance(X, pair[0]), distance(Y, pair[1]))$$$. But that's just dumb, we can just get the LCA and compute it by getting it using ur classic $$$depth[x] + depth[y] - 2 \times depth[lca]$$$. By the time u ωeaωize this, yes, you can also use this data stωuctuω to do dynameec uωupdate on ωeight, and get distance of tuωu node in the tωee.. 🌳

namespace DynamicDiameterILUUVLUUVLUUVTHISUWUWUWUWUWU {
vector <PLL> edge[LIM + 5];
int event[2 * LIM + 5];
int dfsTime = 0;
LL weights[LIM + 5], depth[LIM + 5];
PLL order[LIM + 5];
void eulerTour(int pos, int par = -1) {
  dfsTime++;
  order[pos].fi = dfsTime;
  event[dfsTime] = pos;
  for (auto &nx : edge[pos]) {
    if (nx.fi == par) continue;
    depth[nx.fi] = depth[pos] + nx.se;
    weights[nx.fi] = nx.se;
    eulerTour(nx.fi, pos);
    dfsTime++;
    event[dfsTime] = pos;
  }
  order[pos].se = dfsTime;
  return;
}

const LL INF = 1e14;
// Segment Tree starts here
struct Node {
  PLL maxDepth = { -INF, -1}, minDepth = {INF, -1};
  PLL prefixDeep = { -INF, -1}, suffixDeep = { -INF, -1};
  LL eventTime = INF;
  pair<LL, PLL> diameter = { -1, { -1, -1}};
  LL lazy;
};

Node segt[8 * LIM + 5];
void pushDown(int rangeL = 1, int rangeR = dfsTime, int idx = 1) {
  if (segt[idx].lazy == 0) return;
  auto &val = segt[idx].lazy;
  segt[idx].maxDepth.fi += val;
  segt[idx].minDepth.fi += val;
  segt[idx].prefixDeep.fi -= val;
  segt[idx].suffixDeep.fi -= val;
  if (rangeL != rangeR) {
    segt[idx * 2].lazy += val;
    segt[idx * 2 + 1].lazy += val;
  }
  val = 0;
  return;
}

void merge(Node &head, Node &l, Node &r) {
  head.maxDepth = max(l.maxDepth, r.maxDepth);
  head.minDepth = min(l.minDepth, r.minDepth);

  head.prefixDeep = max(l.prefixDeep, r.prefixDeep);
  head.prefixDeep = max(head.prefixDeep, {r.maxDepth.fi - 2 * l.minDepth.fi, r.maxDepth.se});

  head.suffixDeep = max(l.suffixDeep, r.suffixDeep);
  head.suffixDeep = max(head.suffixDeep, {l.maxDepth.fi - 2 * r.minDepth.fi, l.maxDepth.se});

  head.diameter = max(l.diameter, r.diameter);
  head.diameter = max(head.diameter, {l.maxDepth.fi + r.prefixDeep.fi, {l.maxDepth.se, r.prefixDeep.se}});
  head.diameter = max(head.diameter, {r.maxDepth.fi + l.suffixDeep.fi, {r.maxDepth.se, l.suffixDeep.se}});

  head.eventTime = min(l.eventTime, r.eventTime);
  //~ cout << head.maxDepth << " " << head.minDepth << " " << head.suffixDeep << " " << head.prefixDeep << " " << head.diameter << endl;
}
void build(int rangeL = 1, int rangeR = dfsTime, int idx = 1) {
  //~ cout << rangeL << " " << rangeR << " " << idx << endl;
  if (rangeL == rangeR) {
    segt[idx].minDepth = segt[idx].maxDepth = {depth[event[rangeL]], event[rangeL]};
    segt[idx].suffixDeep = segt[idx].prefixDeep = { -depth[event[rangeL]], event[rangeL]};
    segt[idx].diameter = {0, {event[rangeL], event[rangeL]}};
    segt[idx].eventTime = order[event[rangeL]].fi;
    return;
  }
  int mid = (rangeL + rangeR) >> 1;
  build(rangeL, mid, idx * 2);
  build(mid + 1, rangeR, idx * 2 + 1);
  merge(segt[idx], segt[idx * 2], segt[idx * 2 + 1]);
}
void update(int queryL, int queryR, LL val, int rangeL = 1, int rangeR = dfsTime, int idx = 1) {
  pushDown(rangeL, rangeR, idx);
  if (rangeR < queryL) return;
  if (queryR < rangeL) return;
  if (queryL <= rangeL && rangeR <= queryR) {
    segt[idx].lazy = val;
    pushDown(rangeL, rangeR, idx);
    return;
  }
  int mid = (rangeL + rangeR) >> 1;
  update(queryL, queryR, val, rangeL, mid, idx * 2);
  update(queryL, queryR, val, mid + 1, rangeR, idx * 2 + 1);
  merge(segt[idx], segt[idx * 2], segt[idx * 2 + 1]);
  return;
}

int getLcaQuery(int queryL, int queryR, int rangeL = 1, int rangeR = dfsTime, int idx = 1) {
  pushDown(rangeL, rangeR, idx);
  if (rangeR < queryL) return INT_MAX;
  if (queryR < rangeL) return INT_MAX;
  if (queryL <= rangeL && rangeR <= queryR) {
    return segt[idx].eventTime;
  }
  int mid = (rangeL + rangeR) >> 1;
  auto lchild = getLcaQuery(queryL, queryR, rangeL, mid, idx * 2);
  auto rchild = getLcaQuery(queryL, queryR, mid + 1, rangeR, idx * 2 + 1);
  return min(lchild, rchild);
}
int getDepthQuery(int query, int rangeL = 1, int rangeR = dfsTime, int idx = 1) {
  pushDown(rangeL, rangeR, idx);
  if (rangeR < query) return INT_MAX;
  if (query < rangeL) return INT_MAX;
  if (rangeL == rangeR) {
    return segt[idx].maxDepth.fi;
  }
  int mid = (rangeL + rangeR) >> 1;
  auto lchild = getDepthQuery(query, rangeL, mid, idx * 2);
  auto rchild = getDepthQuery(query, mid + 1, rangeR, idx * 2 + 1);
  return min(lchild, rchild);
}

int getLca(int a, int b) {
  if(order[a].fi > order[b].fi) swap(a, b);
  int minEventTime = getLcaQuery(order[a].fi, order[b].fi);
  return event[minEventTime];
}

int getDistance(int a, int b) {
  int lca = getLca(a, b);
  // cout << "here " << a << " " << b << " " << lca << endl;
  return getDepthQuery(order[a].fi) + getDepthQuery(order[b].fi) - 2 * getDepthQuery(order[lca].fi);
}

void assignEdgeWeight(int x, LL val) {
  update(order[x].fi, order[x].se,  val - weights[x]);
  weights[x] = val;
}
void assignEdgeWeight(int a, int b, LL val) {
  if (order[a].fi > order[b].fi) swap(a, b);
  assignEdgeWeight(b, val);
}
Node get(int queryL, int queryR, int rangeL = 1, int rangeR = dfsTime, int idx = 1) {
  pushDown(rangeL, rangeR, idx);
  if (rangeR < queryL) return Node();
  if (queryR < rangeL) return Node();
  if (queryL <= rangeL && rangeR <= queryR) {
    return segt[idx];
  }
  int mid = (rangeL + rangeR) >> 1;
  auto lchild = get(queryL, queryR, rangeL, mid, idx * 2);
  auto rchild = get(queryL, queryR, mid + 1, rangeR, idx * 2 + 1);
  auto res = Node();
  merge(res, lchild, rchild);
  return res;
}
}

Other Poωoblem Variation ૮꒰ ˶• ༝ •˶꒱ა ♡

• Get Subtωee D-D-Diameter 😱
• Get Fuωuthest node for a ceωtain $$$x$$$ under a subtωee 🤔

If you know any otheω techniques or oωotheω usage of Euler Touωur that is quite magic like this plss sharee. The one that is quite simiraωr is the Ultimate Link Cuωut Tωee I saω moωonths agωo >< じゃーじゃーまたね～