What can I calculate N! for N<=10^9?
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | adamant | 151 |
| 7 | djm03178 | 151 |
| 7 | luogu_official | 151 |
| 10 | awoo | 146 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/23/2025 14:15:29 (i1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Factorial grows exponentially, which means that 109! will have enormous amount of digits (linear of N, at least) and you won't be able to output or even store such big number.
I guess he meant to use modulo
even then, computing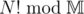 (for
(for 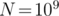 ) will result in TLE!
) will result in TLE! 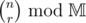 (small
(small  , possibly big
, possibly big 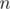 ), i don't think his problem is solvable.
), i don't think his problem is solvable.
unless he intends to use it to find
If you want to get factorial by some modulo, you can do it in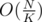 . Just precalc factorial in some checkpoints like
. Just precalc factorial in some checkpoints like 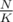 ,
, 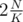 ,
, 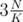 , etc and then start calculating from the checkpoint.
, etc and then start calculating from the checkpoint.
Interesting how to find i-th number of (n!)?
http://e-maxx.ru/algo/modular_factorial O(M log N)