431A - Черный квадрат
В этой задаче нужно было просто сделать то, что написано в условии.
for i = 1 .. s.size()
if (s[i] = '1') ans += a[1];
else ...
Асимптотика: O(N)
Решение: 6676675
431B - Очередь в душ
В этой задаче, в следствии маленьких ограничений, можно перебрать все перестановки и среди всех перестановок выбрать ту, в которой ответ получается наибольший.Легче всего это было сделать использую стандартную процедуру (для С++) next_permutation либо же просто написал 5 циклов. Для каждой перестановки можно было как промоделировать процесс описанный в условии, так и заметить что первый студент со вторым и второй с третьим будут общаться 1 раз(за все время которое они будут стоять в очереди), а третий с четвертым и четвертый с пятым 2 раза. Остальные пары студентов между собой общаться не будут.
Асимптотика: O(n!)
Решение: 6676695
431C - k-дерево
Эта задача может быть решена методом динамического программирования.
Пусть Dp[n][is] — количество путей длины n в к-дереве, в котором если is = 1 — есть ребро веса не меньше d, is = 0 — веса всех ребер меньше d.
Начальное значение Dp[0][0] = 1.
Переход — перебрать ребро из корня которым начинается путь, тогда задача сведется к аналогичной но уже для меньшей длины пути (поскольку поддерево сына вершины абсолютно такое-же к-дерево).
Dp[n][0] = Dp[n-1][0] + ... + Dp[n-min(d-1,n)][0] Dp[n][1] = Dp[n-1][1] + ... + Dp[n-min(d-1,n)][1] + (Dp[n-d][0] + Dp[n-d][1]) + ... + (Dp[n-min(n,k)][0] + Dp[n-min(n,k)][1])
Смотрите решение для уточнения деталей.
Асимптотика: O(nk)
Заметим что это решение, подсчитав частичные суммы, можно очевидным образом модифицировать до O(n), но этого в задаче не требовалось.
Решение: 6676700
431D - Случайное задание
Будем искать n бинарным поиском. Такая функция будет монотонна,поскольку количество чисел с ровно k единичными битами на отрезке n + 2 ... 2·(n + 1) не меньше чем количество таких чисел на отрезке n + 1 ... 2·n. Справедливость предыдущего утверждения следует из того, что n + 1 и 2·(n + 1) имеют одинаковое количество единичных бит. Для нахождения количества чисел на заданном отрезке L...R у которых ровно k единичных бит, нам достаточно научиться считать это количество для отрезков вида 1...L, тогда ответом будет F(1...R) - F(1..L - 1).
Поймем как считать F(1...X). Переберем в каком бите(начиная от старших к младшим) число будет отличаться от X. Пусть первое отличие в i-ом бите(только если в X — этот бит единичный, потому что число не может превышать X).Тогда все остальные младшие биты мы можем выбрать как угодно, при условии что общее количество единичных бит будет равно k. Это можно сделать Cik - cnt способами, где cnt — количество единичных бит в числе X с номерами большими i, а Cnk — биномиальный коэффициент. Так же нужно не забыть про само число X (если в нем, конечно, ровно K единичных бит).
long long F( X )
Ans = 0 , cnt = 0;
for i = Max_Bit...0
if (bit(X,i) == 1) Ans += C[i][K - cnt] , cnt ++;
if (Bit_Counts(X) == K) Ans ++;
return Ans;
Асимптотика: O(log2(Ans))
Решение: 6676713
431E - Химический эксперимент
Разберемся сначала в условии.
У нас есть n колб. В начале в каждой из них налито определенное количество ртути. Надо уметь выполнять два вида действий:
- Сделать количество ртути в p-й колбе равным x.
- Дано число v — это количество воды, которую надо оптимально разлить по этим колбам. Что значит оптимально? Надо в некоторые колбы долить воду так, чтобы среди всех колб, куда мы налили хоть какое-то количество воды, максимальный объем жидкости(вода + ртуть) был как можно меньше.
Ну собственно теперь перейдем к решению.
Используем бинарный поиск для нахождения ответа, в частности, будем перебирать количество ртути в колбе( пусть оно равно d), такой что в меньшие по объему колбы можно разлить все v литров воды, так, чтобы максимальный уровень жидкости не превысил d. Пусть количество колб объемом ртути, меньшим чем d равно t.
Теперь задача свелась к тому, чтобы научиться считать суммарный объем воды который нужно долить в каждую из t наименьших колб, чтобы уровень жидкости в каждой из них стал равен d.
Пусть a[i] — суммарный объем ртути в колбах в которых ровно i литров ртути и b[i] — количество колб в которых объем ртути равен i. Тогда t = b[0] + ... + b[d - 1] и v1 = t * d - (a[0] + a[1] + ... + a[d - 1]) — суммарный максимальный объем воды который можно долить. Если v1 < v, то очевидно этого места мало чтобы разлить всю воду, иначе вполне достаточно и значит ответ уже будет не больше d.
После того как мы нашли такое наименьшее d, мы можем утверждать что ответ равен d — (v1 — v)/t.
Чтобы быстро искать a[0] + a[1] + ... + a[d - 1] и b[0] + ... + b[d - 1], а также выполнять запросы первого типа можно использовать дерево Фенвика.
Асимптотика: O(qlog2(n))
Решение: 6676668
1337 рейтинга, норм
Недостаточно прав для просмотра запрошенной страницы. На все решения. -(
Кстати, в задаче С динамика d[sum][maxedge], на мой взгляд, более очевидна, чем динамика d[n][is].
I clicked the solution link and got "You are not allowed to view the requested page" :P
fixed
KaiZeR just made Guinness world records for fastest editorial posting :P .
Thanks. It will have been made when I publish an editorial for E.
Is there any better solution for Problem B...?? If the input was big then how do we solve it.?? Any idea please.. :D
How can we prove that function is monotone in problem D?
I have written it in editorial. Please, re-read it more attentively.
Oh, got it, Truly nice observation. ty :)
По Е заходит корневая по запросам, 6674771 — для нее не нужен ни фенвик, ни декартово дерево, ни дерево отрезков, все нужные значения можно искать бинарными поисками.
Problem C can also be solved this way. We can calculate total number of n weighted paths using DP. Also calculate number of n weighted paths with no path having edge >= d. Subtract the second value from the first one.
Thank you man. Your solution is easy to understand. I saw your solution. I didn't understand the editorial, but I understood after reading your comment and your solution. Many many thanks...
great
Can someone explain me why i'm getting WA with this solution : 6676798 using dp to count all the paths using edges with weight k or lower :
and then doing the same for k=d-1
and the answer will be dp[n]-dpp[n] % 1000000007
got it it was just about doing % in the right place :|
I lost a lot of time on problem C. And I didn't manage to finish it in time. Thanks God that you have posted the editorial so quickly. I can't stand to finish solving this problem :))).
For Problem C, i am getting a Time Out with this implementation
unsigned long long ans = 0; const int mod = 1e9 + 7;
void foo( int c, int n, int k, int d, bool take) { if (c == n && take) { ans++; if (ans >= mod) ans %= mod; return; } if (c >= n) { return; }
}
int main (int argc, const char * argv[]) { int n,k,d; ans = 0; cin>>n>>k>>d;
}
Can someone kindly tell me what is the Complexity of this code ?
Since you didnt use memo, your program can run up to o(k^n)
Is it possible to download the test cases somewhere? My solution fails on #28 on one query, and I think there's a bug in my data structure but I can't find it.
It is not possible to download the test cases from codeforces ... but i may suggest u to generate some random cases and run it on any accepted code on ur pc and spot the difference with your code's output on the same cases
I was using a slightly modified version of R-B trees that I've used before. I've done a lot of stress testing on random inputs and it worked correctly. The bug only appears in one test case on one particular query — all queries before and after that are solved correctly, which is very strange.
I guess I could try to submit fake solutions that would print out the first N numbers of the test case in question, then the next N etc, but that would take quite a while..
Ouch it turns out a function called count_less was actually counting elements that are less than or equal, which wasn't an issue in a different problem where elements were unique =\ Good times, failing two problems because of one symbol =(
Can someone explain the solution for Problem E? What sort of structure do I need here to efficiently handle the update and answer the queries at the same time?
segment trees?
Maybe.
What I don't get is, when a query occurs, they need the array h to be sorted to do a binary search for the desired answer.
But the array is changing with every update.
So how are they doing a b.search and dealing with a seg tree at the same time?
I've probably got the idea wrong. :-/
A binary search tree works well for such problems, as you can easily add count/sum to every node. They are a pain to implement, but if you can write them once it can help with future contests. Same goes for other common algorithms such as MCMF, suffix trees.
I haven't yet tried keeping a code library. Hopefully will start working on one soon. :) Although the suffix array code from a previous problem did come in handy in the last two rounds.
Actually, any data structure to find sum and update in a logarithmical time. Some of them, with pre-processing of input, like a "squeeze coordinates".
With the help of Xellos's comment, I think I get the idea now. Thanks.
I don't know about efficient, but you can read all the numbers, split them (in sorted order) into
groups of 
numbers (ignoring duplicates) and remember the sum of numbers present in each group. Removing/adding a number takes 
time, since just 1 group is updated for either action. Answering query 2 means flooding the array and finding the height of water surface afterwards, so you need to find the x such that when the smallest x elements are flooded, the water surface would reach above the x-th but not above the x + 1-st element; that can also be done by adding whole groups of numbers to the x flooded numbers and when we can't add a group, then adding its elements. Time complexity: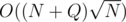 
.
Thanks a lot. :) That looks like a convincing algorithm for this problem.
The issue of using segment tree is how to avoid resort all the elements.
My idea is instead storing the value of each tube, you store pair<V,Q> which means there are Q(quantity) tubes that has the value V. Since there are up to 100000 tubes and up to 100000 ops, there will be at most 200000 different values, means at most 200000 pairs<V,Q> are needed.
At first, find out all possible values which takes up to O((n+q)log(n+q)) time(using binary search), then build all the pairs and sort them by V. Now you can build a segment tree on it.The tree will track both the sum total value(sum total value of a pair = V*Q) and sum Q.
For every update, you only need to change the Q without resorting the pairs. do binary searches on V to find the pairs where you need to Q+=1 and Q-=1 (of course to you need to track the value of each tube to find out the current value of the specified tube),then modify the segment tree. For every query it's easy to do since we are using segment tree.
:) I just coded your algorithm, and it's so hard for me to implement. It's my first time though. 6685388
i guess problem E is O((q+n)logn)...
I used a different idea for D. Ofcourse, the only reason it didn't pass in contest was because i set upper limit of binary search, hi = 1e18 / 2 when in fact it should be just hi = 1e18. (Making this change passed it in practice).
To make it easier to explain, let's call those numbers which have exactly k 1-bits in their binary representation as good numbers.
Let's consider the binary representation of N to be xxxx. Now, 2 * N will look like this: xxxx0.
Observe that for every good number < = 2 * N such that its 0-th bit is set to 0, there exists an identical good number < = N (by just doing one right shift).
Now, let's say f(X) = Number of good numbers < = X.
Since we are calculating f(2 * N) - f(N), those good numbers < = 2 * N which have 0-th bit set to 0, will not be counted as there exists an identical counterpart < = N.
Therefore, f(2 * N) - f(N) = number of good numbers < = 2 * N whose 0-th bit is set to 1 = g(N) (say)
g(X) is now monotonic and now binary search can be applied to find the number which has m good numbers less than it.
I just realized f(2 * N) - f(N) is monotonic. bangs head on the keyboard
My solution is like your solution: 6678236
Why does this solution to E (using treap) give Memory Limit Exceeded? :(
don't know, but obvious mistake is
#define N 100005Sorry I don't get it; why is that a mistake?
When you're freeing a node you're not putting it back into the pool, so you need at least 200000.
Ah! Thanks. Still MLE though
http://codeforces.net/contest/431/submission/6680373
I can't understand the solution of problem D. Could someone explain it clearly?
What is not clear, tell more exactly please.
Calculating how many numbers have k 1 bits in the range [1.....x]
Number X we will analyze separately. Other numbers in range 1...X - 1 smaller then X, so their binary representation have difference with X. We can divide they into groups by the number of first(largest) bit, which is such, that this bit in X is not equal to correspondent bit in all numbers of this group. Its obviously to understand, that any two of this groups do not intersect. To calculate all this numbers we can iterate all this groups, and calculate it only for each group separately. If we know bit with the first difference with X, we can choose another(smallest) bits in any way(so the size of group is 2i. But we need only the numbers with exactly k 1 bits, co we can do this in Cik - cnt ways.(notation the same as in editorial)
Got it. Thanks.
Thanks for the explanation...
Thanks :) . Was having a hard time . Now its completely clear :)
Can someone explain me why this solution 6681438 get WA #4
I've slightly changed your binary search and removed bit count for initial result and it's worked 6689653;
I still haven't been able to understand the problem statement of problem E. So please explain what are we supposed to do in case of a query of Type 2 ? :(
As query 1 is
H[p] :=v, query 2 asks you to find the minimum height of water surface you can get by pouring v units of water into the tubes in some way.Thanks for the explanation.
You will choose a subset of the tubes and distribute a total of v liters of water among them.
Among the chosen subset of tubes ... you need to find the volume of the tube with maximum amount of liquid (mercury + water) (let's name this volume x)
This of course depends on the amount of water added to each tube and the amount of mercury initially at each tube before processing that query ... So You choose the subset of the tubes and distribute the water among them in order to minimize that value x.
The query of type 2 ... asks for the minimum possible value of x.
For Problem E, can we make a BST to get the Kth number in the sequence and then binary search the number K? Then we can know how many we should pour to every tube. Or I didn't understand the meaning of the problem? Will it get TLE?
Yes we can do in such way. It is the similar to the solution described in editorial, but only we searching for the volume in Kth tube, instead of the K. It will get OK)
Thx:)
(Комментарий удалён автором, в связи с негативной реакцией общественности и отсутсвием позитивных отзывов.)
Разобравшись в предлагаемом (6676700) коде, я понял, что непонятную для меня формулу можно было записать следующим образом, чтобы она отражала идею алгоритма:
Dp[n][0] = Dp[n-1][0] + Dp[n-2][0] + ... + Dp[n-DL][0], гдеDL = min(d-1,n).Аналогично, вторая формула превращается в следующую:
Dp[n][1] = Dp[n-1][1] + Dp[n-2][1] + ... + Dp[n-DL][1] ++ (Dp[n-d][0] + Dp[n-d][1]) + (Dp[n-(d+1)][0] + Dp[n-(d+1)][1]) + ... + (Dp[n-K][0] + Dp[n-K][1]), гдеK = min(k,n).То же самое можно представить в другом виде (убрав зависимость от DL и суммируя
is=1иis=0отдельно):Dp[n][1] = Dp[n-1][1] + Dp[n-2][1] + ... + Dp[n-K][1] ++ Dp[n-d][0] + Dp[n-(d+1)][0] + ... + Dp[n-K][0].Update: changed
i(used in source code) ton(used in editorial explanation).Del
(Комментарий удалён автором, в связи с негативной реакцией общественности и отсутсвием позитивных отзывов.)
Спасибо за Ваши комментарии. Постараюсь ответить сразу на все.
1) Да, Вы правы в ограничениях была допущена оплошность. Но к ошибке она не привела, вероятно из-за особенностей использования памяти С++. Да, кстати, макс тесты в задаче есть. Предложу свою версию, но могу ошибаться, так что не было бы лишним мнение эксперта в этом вопросе. Обращаясь к 100-му элементу массива мы действительно вылазим за область зарезервированной памяти и записываем значение куда-то. Но вследствие того, что никаких дополнительных переменных мы не создаем да и вообще не меняем ту область памяти, куда залезли, обращаясь к dp[100][0], записанное туда значение сохраниться.
2) По поводу суммы. Нет, ошибки там нету. Разве что многое предполагалось очевидным. Например то, что сумма берется по спаданию первого индекса, или что брать ребро весом больше чем длина пути — не нужно( соответствующие значения просто будут равными 0, ведь нету ни одного пути отрицательной длины). Приведенная формула написана для лучшего понимания того, каким образом будет делаться переходы динамики, и не претендует на формальную безупречность. Ведь надеюсь общая идея понятно? А для уточнения деталей как раз и выкладывается код авторского решения.
3) Ну можно и заменить. Для понимания может быть так и лучше но количество итераций от этого не уменьшиться. Да и вообще, уверяю Вас, вы не заметите никакой разницы на практике, тем более с таким-то ограничениями.
431E — Chemistry Experiment: In order to be able to use Fenwik tree — you had to re-map large mercury volume values to the smaller range — why not just limit all volumes in the input to 100K or so???
Can someone explain the solution of problem C in a little bit more detail. I am unable to understand the DP part mentioned in the editorial.
The DP part refers to dynamic programming method of solving the task.
The method proposed in the editorial suggests to regard a subproblem
Dp[n][is]where:nhas same meaning (total weight of a path) as in the problem description except for its range (0 <= n <= 100).Dp[n][0]is the number of paths of total weightnif we revert thed-condition (here we can use only those edges which weight is strictly less thand).Dp[n][1]is exactly what is asked for in the problem description (considered paths are all possible ones such that each of them has one or more edges with weightdor larger).Note that the sum of both (
Dp[n][0] + Dp[n][1]) is the number of all possible paths of total weightn(i.e. without thed-restriction).Dp[0][0] = 1Dp[0][1] = 0I believe that according to the solution (6676700), more exact formulas could be expressed as:
Dp[n][0] = Dp[n-1][0] + Dp[n-2][0] + ... + Dp[n-DL][0]whereDL = min(d-1,n).Dp[n][1] = Dp[n-1][1] + Dp[n-2][1] + ... + Dp[n-K][1] ++ Dp[n-d][0] + Dp[n-(d+1)][0] + ... + Dp[n-K][0]whereK = min(k,n).I'm not sure I can clearly explain in English the reasoning which lies behind the formulas. Below is my best try.
Assume we have already calculated (somehow) the
Dp[i][0]for all values ofilesser thann. Now we want to calculateDp[n][0]. We can think ofnas a number with the following possible decompositions:(n-1) + 1,(n-2) + 2,(n-3) + 3, ...,(n-m) + m. Now let's think ofmas a weight of one single edge. (Honestly, it is not yet clear to me why it is sufficient to regard only the case when we add only one edge. Could someone else explain this part please?)So, we can state that we have
mdifferent values of weight of an edge. Given any specific value ofmwe can addDp[n-m][0]different paths (to the edge of weigthm) to get the total weight of exactlyn. Now it is obvious that by adding togetherDp[n-m][0]taken for each possible different values ofmwe will get theDp[n][0]value. This is exactly what formula forDp[n][0]is about.Now all we have to do is to determine the range for values of
m. According to the possible values of the first index ofDp[][], this restriction should apply:n-m >= 0. Thus,m <= n. According to the definition ofDp[][0],mmust be less thand, i.e.m <= d-1. Minimum value formis obviously1. Resulting range is:1 <= m <= min(d-1,n)(seeDLabove). Alternatively, we could defineDp[n][0]as zero for all negative values ofnand consider1 <= m <= d-1.Explanation of the formula for
Dp[n][1]is a bit more complicated but the logic behind it is similar. I believe that if one understood the explanation forDp[n][0]then it would not be hard to extend similar approach toDp[n][1]. (Or, maybe, I'm just too lazy to explain it in full -- SMILE).I hope this will be useful for someone.
My related comment (in Russian)
Update: wrong value for Dp[0][0] was fixed (misprint).
Do you know how to solve the simpler problem, without the d restriction, using simple O(nk) dynamics? Once you got that, assuming f(n,k) is the number of ways to break n into a sum of integers from 1 to k, the answer is simply f(n,k)-f(n,d-1).
I think there is a typo in the English version of editorial of problem E.
"such that in the tubes with smaller volume of the liquid can be poured all v liters of water and the minimum liquid level do not exceed d."
I think it should be "the maximum liquid level doesn't exceed d".
Someone told that B can be solved in O(N2). Can anyone please explain me about this solution?
I don't think that's possible. If you consider the permutation as a path in a graph (where each student is a vertex), you need to find the path that contains each student exactly once, and the weight of the first two edges, plus two times the weight of the next two edges, plus three times the next two, etc, is the highest. This is very similar to Travelling salesman problem, which is NP-complete.
Now this may be an overkill but can someone please explain this in 4..
"Iterate number of bit will be the first(from biggest to smallest) which have difference in X and our number, which amount we want to calc. Let's first difference wiil be in i-th bit(it's possible, if in X this bit equals to 1, because our number does not exceed X). Then other smallest bits we can choose in any way, but only general number of one bits will equals to k. We can do this in Cik - cnt ways, where cnt — the number of one bits in X, bigger then i, and Cnk — binomailany factor. Finally, you should not forget about X (if it, of course, has k one bits)."
A,2014-05-24 not so nerdy guy here. Any explanation for layman please
Let me try to explain by giving an example say 21(10101).
I'll be using 0 based index for bits. 0th bit represents first bit from the right. We start from the most significant bit(the first one from the left).Now we consider all numbers first where this bit is 0(all those numbers will lie in our range as can be easily seen).So from the remaining bits(to the right of the present bit) we add to the ans number of ways in which we can select k of them.(in this case it will be 4Ck). Now we have to add those numbers in which the 4th bit is 1. This is the same as finding number of ways of selecting k-1 bits from the remaining bits(as we have already selected one). So we decrease k and move forward. Now we encounter a 0(3rd bit). We have already counted all solutions where this bit can be 1 (when we assumed 4th bit to be 0 and both of them cannot be 1 simultaneously as it will exceed the given number) . So this does not contribute(for the lack of a better word) anything more and we can move on. By same logic it can be seen that 0s will not be contributing to the answer. Now the problem is just a simplified version of the original. For this number (101 i.e 5) we have to answer for k-1 as we have already encountered a 1.
What does it mean when you say Y is less than X? It means that for some i, the i-th bit in X is 1, and i-th bit in Y is 0, while all higher bits are equal. That means we can choose all values of i such that i-th bit in X is 1, and calculate the number of ways to set the lower bits of Y to satisfy our condition (of having exactly k one bits).
Можно как-то более-менее легко решить Е в онлайне (если запросы заранее неизвестны и ДО по сжатым координатам написать не получится) быстрее, чем корневой по запросам? Предполагая, что декартово дерево писать настроения нету:)
6677544
Да, можно, например двумя битовыми борами за O(Q * log2(maxH)). Идея очень простая. Бинарным поиском переберем ответ. Теперь нужно знать количество чисел не превышающих текущее х, а также сумму всех таких чисел. Будем рассматривать 2 одинаковых бора. В каждой вершине будем хранить как раз эти 2 параметра (количество терминальных вершин в поддереве, а также суму чисел, соответствующих им). Теперь когда мы хотим добавить число — мы его добавляем в первый бор, а когда хотим удалить — то добавляем во второй бор.
Запрос = запрос к первому - запрос ко второму.
Спасибо, красивая идея)
Ну дерево отрезков (или фенвик) по несжатым координатам тоже никто не отменял :) Еще интересный трюк узнал на этом раунде — фенвик по несжатым координатам это просто тот же фенвик + хеш мапа :)
in problem E,why the finaly answer is not d and is d — (v1 — v) / t? can someone explain (sorr for poor english)
First it finds a level d which is not the actual level. Then the empty space under d is v1. Fill it with v. If total number of tube is t then the actual level'll be at d-x where x = (v1-v)/t;
In the picture as there are 2 bars under d level the actual level is at d-x [ x = (v1-v)/2 ]
it is not optimall that find such d that v1=v ?
May be you can't directly find such d for v1 = v as liquid can be changed at any time.
I realized this,thanks for good explain and for image :)
Знаю, что немного опоздал, но не мог пройти мимо.
Задачу Е можно решать в онлайне деревом отрезков по несжатым числам с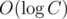
на запрос и 
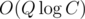памяти и времени суммарно. Для этого просто вместо отдельного бинарного поиска по ответу совмещаем его со спуском по дереву, каждый раз выбирая для спуска то поддерево, которое нам необходимо. Пример решения: 6720129. Скорее всего, такая техника применима и в решении деревом Фенвика по сжатым координатам, но она немного сложнее в реализации и мне слишком лень с ним возиться сейчас :)
UPD: Извиняюсь, по сжатым числам, похоже, за
не делается :)
Please improve your english. I don't understand anything in Problem D editorial.
PS: Is this editorial Google translated from Russian or something? Please stop doing that.
Hi KaiZeR, In your editorial solution to this problem. I do not get the reason for (DP[0][0] = 1). According to me, it should be (DP[0][0] = 0) as we will always have zero paths when sum of path(n) is zero and when d is zero. Can you correct me if i am wrong ??
We have only one way with length equals to 0. This way consists only root.
Can anyone explain me the problem D Example 2 as With N=5 The Range Is{6,7,8,9,10} among these- Only 6 and 10 are having exactly 2 digits 1 but we want 3 numbers than how the answer is 5
6 — 110 +
7 — 111
8 — 1000
9 — 1001 +
10 — 1010 +
There are three numbers.
Can anyone please explain me the test cases 1 and 3 for C ? I'm unable to understand.
Only for test case 3 ?
For the third test case:
1 -> 1 -> 2
1 -> 2 -> 1
1 -> 3
2 -> 1 -> 1
2 -> 2
3 -> 1
Only this ways satisfy the statement.
http://www.hastebin.com/qugasuduji.vala
I am unable to figure out why the above code (same logic as editorial) is leading to WA in test case 7. Could someone please help me identify where I am going wrong?
EDIT: Got it, I used int instead of long long which led to overflow
How to solve C in O(N) with partial sum? Appreciate any help.
My solution to problem C:
Apply dfs on the the tree and store the result in a dp table where dp[i][j] denotes the answer to the tree with sum = i at root and j = 0 or 1 based on whether while reaching the present node I have satisfied the property to have at least one edge having weight>=d.
Solution
P.S. Can anybody tell me how do I implement the same code iteratively?
Here is an Alternate DP solution — 139873483