439A - Деву-певец и Чуру-комик
For checking whether there is a way to conduct all the songs of the singer, you can conduct the event in the following way.
- First singer will sing a song.
- Then during 10 minutes rest of the singer, the joker will crack 2 jokes(each of 5 minutes)
- Then singer will again sing a song, then joker, etc.
- After the singer has completes all his songs, the joker will keep on cracking jokes of 5 minutes each.
Hence minimum duration of the even needed such that sing could sing all his songs will be t1 + 10 + t2 + 10 + ... +tn = sum + (n - 1) * 10 where sum denote the total time of the songs of the singer.
So for checking feasibility of the solution, just check whether sum + (n - 1) * 10 ≤ duration or not?.
If it is feasible, then time remaining for joker will be the entire duration except the time when the singer is singing the song. Hence time available for the joker will be duration - sum. In that time joker will sing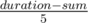 
songs.
Solution codes
You can formulate the problem in following way. Given two arrays a and b. Find minimum cost of matching the elements of array a to b. For our problem the array a will be same as b. The array b will have content x, x — 1, , 1, 1. For a general version of this problem, we can use min cost max flow(min cost matching), but for this problem following simple greedy solution will work.
- Sort the array a in increasing and b in decreasing order (or vice versa).
- Now match ith element of the array a with ith element of array b.
Proof:
It can be easily proved by exchange argument.
Solution Codes
439C - Деву и разбиение массива
Let us first try to find the condition required to make sure the existence of the partitions.
Notice the following points.
If the parity of sum does not match with parity of number of odd partitions (k - p) , then we can't create the required partitions. eg. a = [1;2], k = 2, p = 0, Then you can not create two partitions of odd size, because then sum of the elements of the partitions of the array will be even whereas the sum of elements of the array is odd.
If number of odd elements in a are less than k - p (number of required partitions with odd sum), then we can not do a valid partitioning.
If number of even elements are less than p, then we can not create even partitions simply by using even numbers, we have to use odd numbers too. Notice the simple fact that sum of two odd numbers is even. Hence we will try to include 2 odd elements in our partitions too. So if we can create oddsRemaining / 2 partitions in which every partition contains 2 odd elements, then we can do a valid partitioning otherwise we can't. Here oddsRemaining denotes the number of odd elements which are not used in any of the partitions made up to now.
Let oddElements denotes the number of odd elements in array a. Similarly evenElements denotes the number of even elements.
So the answer exists if
- Number of possible odd partitions are ≥ k - p i.e. oddElements ≥ k - p.
- Number of possible even partitions are ≥ p i.e. evenElements + (oddRemaining) / 2 ≥ p. where oddRemaining is oddElements - (k - p).
For generating the actual partitions, you can follow the same strategy used in detecting the existence of the partitions. We will first generate any valid p partitions (forget about the condition of using the entire array), then we can simply include the remaining elements of the array in the last partition and we are done.
Solution Codes
You can solve the problem in two ways.
- By using ternary search
Let us define a function f. Function f(k) = cost needed to make array a elements ≥ k + cost needed to make array b elements ≤ k
Instead of proving it formally, try checking the property on many random test cases. You will realize that f is convex.
Claim: f is convex:
Proof:
It is fairly easy to prove. See the derivative of f.
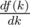= — (# of elements of b > k) + (# of elements of a < k)
The first term (without sign) can only decrease as k increases whereas second term can only increase as k increases.
So,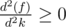 
- By using the fact that optimal values are attainable at the array values:
All the extremum points will lie in the elements from the any of the arrays because f is convex and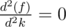 
at the event points (or the points of array a and b).
For learning more about ternary search, you can see following topcoder discussion
Another smart solution
Please see following comment of goovie and proof is given in the reply by himank
Solutions Code
- ternary search solution
- my solution using 2nd fact
- [user:Gerald] solution
- [user:triveni] solution using smart solution
439E - Деву и праздник день рождения
There are two possible solutions.
dp solution
Let P(n, f) be total number of ways of partitioning n into f segments such that each ai is positive. With some manipulations of the generating function, you can find that this is equal to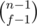 
.
So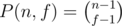 
Let F(n, f, g) denotes partitions of n into f parts such that gcd of all the ai's is g.
Note that F(n, f, 1) = P(n, f) — sum of F(n, f, g) over all possible gcd g's. So g will be a divisor of n.
In other words,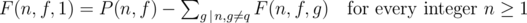 
As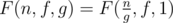 
.
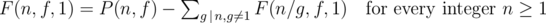
You can implement this solution by a simple dp.
You can pre-calculate factorials which will help you to calculate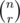 
.
Complexity of this solution will be nlogn over all the test cases.
Mathematical solution
Note that F(n, f, 1) = P(n, f) — sum of F(n, f, g) over all possible gcd g's (g > 1 such that g is a divisor of n.
In other words,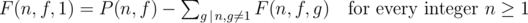 
As F(n, f, g) =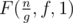 
.
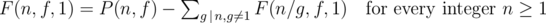
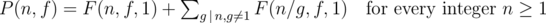
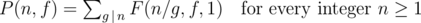
Now you have to use Möbius inversion formula.
Theorem:
If f and g are two arithmetic functions satisfying
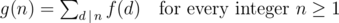
then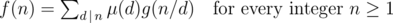 
So In our case: g(n) is P(n, f) and f(n) is F(n, f, 1).
For proving complexity: Use the fact that total number of divisors of a number from 1 to n is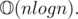 
Please also see xorfire comment for understanding the relation between mobius function and the solution using inclusion exclusion principle.
Solution Codes
got the solution:)
if your solution wasnt hacked during the duration of the contest then it wouldn't have passed the system tests! only way to prevent a solution from getting hacked is to make a perfect solution with no flaws!
This is not true; a lot of people just don't bother to hack so a lot of people, for example, who didn't handle integer overflow ended up failing test 12 on B.
clearing of pretest doesn't mean that your solution is correct. pretest is few test cases which checks your solution. if someone else will see your solution and found it wrong it can hack your solution.
that means... your solution for that problem fails on a test case which the hacker used to test your problem. Your problem gave a wrong answer, so the points you have been awarded are withdrawn (which would anyway become zero in the final system test, if your solution had not been hacked).
Infact this is a good thing. You can resubmit your code by doing necessary corrections , if your problem is hacked. You can submit any number of times in the 2 hour duration unless you locked your solution.
hope this helps....
Hi, how did you find derivative and double derivative there?
It is just found by intuition that "The first term (without sign) can only decrease as k increases whereas second term can only increase as k increases.", so double derivative will be >= 0.
I was just going through different submissions of problem C, and came across this solution 6802980 which shows wrong answer for test case 44, but the output seems correct. Could you kindly tell how is that answer wrong?
Got it. Didnt see the number of elements :)
The output is supposed to be a partition of the given numbers. The output of the given submission contains only 7 numbers, while the original array contained 9.
It would be great if you could add links to solutions which solve the problem using the ideas described in the editorial.
nice idea, I will do it in just an hour :)
I used a random algorithm to solve the problem D. CLICK
Great round setup and nice tutorial. Keep up the good work.
It looks like the editorial for E is intended to scare away people :D
First of all, we don't need generating functions to derive that simple formula for P(n, f). It is well known. We don't need to use a tank to kill a mosquito. :P
And the second thing is that we can use simple inclusion exclusion to derive the mathematical solution rather than use mobius inversion (although it is true that both are the same, since when we are using inclusion exclusion, we are basically reproducing the proof of Mobius' Inversion formula). Just saying it would have been better if you had explained that way.
Nevertheless, nice contest and editorial, hope to see more from you in the future :)
Yes, you are right, I will add your comment in the editorial too.
But that formula allows us making ai = 0. What is the proof that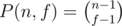
?
If you need number of solutions to a1 + a2 + ... + af = n where ai ≥ 1. It is the same as the number of solutions to b1 + b2 + ... + bf = n - f where bi ≥ 0 simply by substituting bi = ai - 1. Now use the formula given in the link and you end up with the result that you want.
how P(n, f) is equal to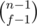
it should be equal to 
according to the link .Please explain.
Read what is given, understand it and then look at my explanation above instead of just looking at the formula and complaining that they don't match.
In the link you mentioned, can you please explain how the balls are matched from the k-1 extra urn to the original n urns??
The link given in the above comment is not working. So here is the updated link.
This is my approach to Problem D.
sort array a in increasing order and array b in decreasing order. Now find a index i such that a[i]>=b[i]. Now all elements from 0 to (i-1) in both a and b can be converted to some value X such that b[i]<=X<=a[i].So
ans = (b[0]+...b[i-1]) -X*(i-1) + X*(i-1) -(a[0]+ ...a[i-1]) = (b[0]+...b[i-1])-(a[0]+ ...a[i-1]).
NOTE: if no index is found till end of any one array then i= min(m,n);
6811074
See this solution(same approach) : solution.
Good idea! I had got something same in my solution, i also sorted arrays in the same way, but i didn't think about such formula and calculated everything step by step... I just understood, that we want to change the smallest amount of numbers as we can. So, every step we have got some already chosen elements in arrays and we think, that they are equal. So, we should choose the array and change chosen elements in it. We can easily see, that we can, for example, increase the elements in first array only to min(b[0], next number in a). If we increase them to b[0], we can stop, if we increase them to next element of a, we should add this next number to chosen elements in a. And, of course, at first, we have got only one element chosen in every array. My solution:6808595
thank you. himank for your smart solution. I was surprised by seeing this solution.
What is 2 pointers approach to problem D?
I don't understand, why E solution has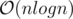
complexity. Can you explain this a bit clearer? (I know, that there are 
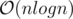pairs of divisors from 1 to n, but I don't understand why it makes this true). Will be very grateful for help.
I am just attaching the solutions in a while, it will be clear then :)
I still don't get it, why the complexity is O(nlogn)?
http://codeforces.net/contest/439/submission/6814322
In the solution above we run through all the divisors of n. But the number of divisors, as I know, isn't O(logn).
Could you please explain this moment?
after four days... still waiting... :{
after 7 years still waiting
after 10 years still waiting
The maximum number of prime divisors n can have is 6(as 2*3*5*7*11*13*17>10^5).
Assuming we use the Mathematical solution, following will be the complexity,
Let us pre-calculate prime factors of all numbers from 1....(10^5) using the Sieve of Erastosthenes(each number has a vector containing the primes that divide it). Complexity = O((nlogn)(loglogn))
Also we pre-calculate factorials and modular inverses uptil 10^5. Complexity= O(nlogn)
Then, for every query, we apply the principle of inclusion-exclusion for upto 6 primes. Complexity = O(t*2^6)
All other things like input etc. can be done in less than or equal to O(n).
So, total complexity = O(nlogn) + O(t*2^6) + O((nlogn)(loglogn)) = O(nlogn)
Do point out if I am wrong somewhere. :)
I have extremly fast and easy solution to D, however I can't find the proof. Here it is:
Sort a increasingly, and b decreasingly. Now, we add to result values (b[i]-a[i]) from left to right while a[i] < b[i].
Here is link to my submission:
http://codeforces.net/contest/439/submission/6809214
I used the same approach and here is the proof.
sort array a in increasing order and array b in decreasing order, now our target is to equate the first element of both the arrays. In order to achieve this a[0] can be incremented maximum up to a[1] and b[0] can be decremented up to b[1] (because if we increment a[0] to a value more than a[1] then a[1] also need to be incremented to that value). If this change in a[0] and b[0] results in a[0]>=b[0] then we are done else do the same thing for next elements until a[i]>=b[i]. so once we find such index i then all elements in a and b below i can be converted to a[i] and b[i] respectively. but instead we can convert elements to some value X such that b[i]<=X<=a[i].
so ans = (b[0]+...b[i-1]) -X*(i-1) + X*(i-1) -(a[0]+ ...a[i-1]) = (b[0]+...b[i-1])-(a[0]+ ...a[i-1]).
very nice explanation!!!
Yes. Fast and easy. that's why yours is mentioned in the editorial.
But, I think that condition should be while(a[i]<b[i]) instead of until.
yes, you are right.
In problem E, do you need to use Fermat's little theorem?
In problem B i used unsigned long long for answer as answer was expected to overflow integer range but n and x is said to be within limit 10^5 then why I got wrong answer in test 12 on using them as int.
I submitted sol. in MvS 2010. Here http://msdn.microsoft.com/en-IN/library/s3f49ktz.aspx range given for integer is –2,147,483,648 to 2,147,483,647.
The problem is when you use int operands, the result of the operation (in your case it is "*") is also computed as int. Then, when it is evaluated, it is assigned to your long long variable, but the overflow already occured.
It seems that using the standard Arrays.sort in Java will give TLE in problem B... Of course, radix sorting could also be used. However, one would expect this sort to be enough, given the constraint on the array size. Also, it seems kind of unfair because the C++ sort seems to have no problem.
Why don't you write your own sorting algorithm that guarantees logarithmic time.
or just use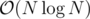
.
Collections.sort(), which uses merge-sort, therefore runs inYou have big integers in Java, don't forget that it is unfair too :-)
My code for problem C keeps giving WA !!
Any help please :/
learn more while reading the editorial than taking part in the contest! Thanks for such perfect proofs~!
PraveenDhinwa,Can we say that the greedy approach of the second problem is actually an outcome of the rearrangement inequality??
I didn't understand you, The greedy approach can be proved by exchange argument(ie we will always get greater answer if we do the sorting as given in the problem statement), Try on any 2 elements arrays and generalize it.
Yes, this is exactly what the rearrangement inequality states (http://en.wikipedia.org/wiki/Rearrangement_inequality)
Lewin,Thank you :) .. PraveenDhinwa,that's what I was trying to say that this exchange argument thing is basically same as rearrangement inequality(proof of which is also based on similar logic).nothing else.
And thanks for providing an awesome problem set like you have always done in the past :)
Yes, you are right, both the things are same.
I am glad that you liked the contest :)
439B - Деву-дурачок
Why does this solution (6815744) give TLE while this does not (6815855)?
plz refer to following comment
439B - Деву-дурачок
Why does this solution (6815744) give TLE while this does not (6815855?
Because in Java : default types like int arrays are sorted in N^2 time, while user-defined type eg Integer arrays are sorted in nlog(n) time.
the ternary search solution for problem D, the author made "it"(the variable name in the code) from 0 to 100 ,why it max value is 100, but not 200 or 50? i think the max value for it is the cubic root of 10^9. can you help me ?
it should be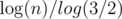
= 51.0 Try running your program for 49, 50, 51, 52 and check on which iteration it gets accepted :)
Hi, praveen123. I had the same solution in problem 2 as yours, but in C, not C++. And it was wrong in 8. I used long long int for result. Isn't it enough? And what data type I must use for such problems in C? Thank you. P.S. I'm a newbie, so my question can be stupid :)
Here is the thing.
int a; int b;
long res = a * b;
if a is around 10^5 and b is also around 10^5. a * b will be overflowed and wont be 10^10.
Try running this and you will get the reason :)
sory.. get it :)
One of the best tutorials, I have read on CodeForces. Thanks for the contest and the editorial !
My worng answer information is: wrong output format Unexpected end of file — int32 expected Could anyone tell me what does this mean?
This means that you did not output anything when a 32-bit integer (normal integer) was expected. Eg : Correct answer : 2 2 Your answer : 2
Thanks!
It is possible to solve this problem B using PHP? I got "Time limit exceeded on test 30". Still, Nobody solve it using PHP. :(
With
bcaddI think you have no hope on success. It is quite slow.Try instead summarize using general numbers. They wrap to
doublein PHP so if answer fit into10^15you will succeed.UPD: No, does not work — too big numbers. However you can try splitting integer in two 32-bit parts :)
Could any body tell me why this greedy assumption would fail concerning problem D? http://codeforces.net/contest/439/submission/6821455
Can someone tell me why this code got TLE?
Every function
. Meanwhile it used recursively, so it will run again and again in 
.
solveis called, it runTry iteration (non-recursive) style and got AC.
Somebody have links for problems with mobius function ?
May be similar to problem E.
Thanks in advance.
(E) part int modpow(int a, int b){ int ans = 1; while(b){ if(b & 1) ans = (ans * li(a)) % mod; a = (a * li(a)) % mod; b >>= 1; } return ans; } int rev(int v){ return modpow(v, mod — 2); } Why are we using (mod-2) ? thanks in advance
modpow(v, MOD — 2, MOD) is computing v - 1 mod MOD, where MOD is prime.
Why 1/v is equal to modpow(v, MOD — 2, MOD) ?
By Fermat's theorem ap - 1 = 1 mod p.
Multiply both sides by a - 1,
we get ap - 2 = a - 1 mod p
Why don't we divide by the factorial instead of calculating inverse and multiply ? int ans = (f[n] * 1LL / f[k]) % mod; ans = (ans * 1LL /f[n — k]) % mod;
Notice that answer must be mod by 1e9+7. Some factor may lost within this operation
PraveenDhinwa I implemented the first solution Java and it does't get AC. I spent more than 1 hour optimizing it each time bumping me up by 5-10 test cases but now I TLE in case 53 and there is nothing else I can add.
P.S.: Similar C++ solution pass 6834876
Time limit is quite relaxed in the problem. So I think your time complexity is more than expected one. My C++ solution passes under .6 or .7 sec.
You are using two loops over factors, this might be the reason behind TLE, though I am not sure about that.
P.S. The code which you have attached is in Java, can you please the C++ one?
How can I loop less than twice??? I need to compute the dp for the factors themselves so I need to loop over their factors. I process them in order so the factors of the factors have their dp there already. Case 53 is just 98280 repeated 100k times. It's weird to have the max case that frequent. This http://codeforces.net/contest/439/submission/6814322 is the solution you refrences in the blog and it's just a recursive form of mine (which would be even slower on java). It passed in 2 sec so it's very hard for Java solutions to pass with this idea. I pushed the optimization as hard as I can. The only thing left is to cache the answers themselves (since I saw the case) but it doesn't feel right.
yes, you are right. You need to loop twice.
Regarding the time limit, it seems like your solution is quite close to time limit. Actually time limit was decided on the basis of mobius solution which will be faster than this. I am sorry but it looks like here you dont have any choice than shifting to mobius solution.
I see. I saw more comments (at least one) asking my same question. I think you should mention it in the editorial. Thanks for your quick responses :)
I have mentioned it in the editorial, thank you :)
Ignore.
Well, as i can see from this solution, it's dp, Java and AC.
UPD. Submitted your solution with Java 8 — AC with 4 sec.
This is exactly what I mentioned in my comment. There is one more optimization which is to cache answers as they are (e.g. f(n,f)) which will only work in case you are repeating queries but this doesn't feel right and shouldn't be part of the solution.
Long Key = (( Long ) N << 32 ) + F ; if ( cache . containsKey ( Key )) { return cache . Get ( Key ); }What? Memoization shouldn't be a part of lazy dp? It's very common technique, must have as it is. (with your logic every code should pass, despite the effectiveness, lol) Secondly, your solution passed under Java 8. Try to use all compilers before blaming the authors about TL.
Can you please read the solution explained above?? The dp is not across cases, it's per case and this is what's explained in the tutorial. Yes the final solution pass on Java 8 but this is after spending nearly an hour of optimization (not doable in contest)
He did EXACTLY what's been said in the tutorial, and did it effectively. Tutorial is only a model solution, it's not like, do this, and this, write this code here. It's your job to make EFFECTIVE code, not just copy paste what's been said, and, afterwards, complaining about wrong verdict. It's like you never solved the problems with multitests, cashing the cases to not calculate them again is like obvious, how can it not feel right?
The reason behind the complexity being nlogn is that the sum of factors over all numbers from 1 to n is nlogn. However, if you refuse to memorize the answers across different queries, it can very easily be made to cross nlogn by using a number which has high number of factors.(although memorization won't help if we change f in every case) Hence, it is advisable to memorize the answers across the queries!
Hi! In problem E second query , isn't it possible partition [5,2] not [5,3] ?
Can we use binary_search for the problem 439D — Devu and his Brother? My solution is going wrong when I apply binarysearch. Can you help me find a mistake in it. Link to my solution: Your text to link here... Thanks in advance.
.
In problem D:
Proof of why optimal values(pivot value) will always lie on array elements, a[i] or b[j]: (here Optimal value is x such that all a's >= x and all b's <= x)
Let a and b be sorted in increasing order. Let us pick a[i] and b[j], such that a[i] < b[j] and there is no element of either arrays in between them. Let cost[z] defines the answer, with z being the optimal value.
Claim: min(cost[a[i]], cost[b[j]]) <= cost[p] for any a[i] < p < b[j].
Proof:
Let count of array 'a' elements before i be $$${n_1 - 1}$$$, and count of array 'b' elements after j be $$${n2 - 1}$$$. Let $$${cd_1}$$$ be cost of converting smaller these $$${n_1 - 1}$$$ elements to a[i] and $$${cd_2}$$$ be cost of converting these larger $$${n2 - 1}$$$ elements to b[i].
Pick $$${p}$$$ such that $$${a[i] < p < b[j]}$$$. And let $$${x = p - a[i]}$$$, $$${d = b[i] - a[i]}$$$,
$$${=> b[i] - p = d - x}$$$
So,
Converting all a[q] to a[i] s.t $$${q < i}$$$, all b[q] to b[j] s.t. $$${q > j}$$$, and then push all $$${n_2}$$$ elements towards a[i], we will get cost[a[i]] i.e.:
$$${c_1 = cost[a[i]] = cd_1 + cd_2 + n_2d}$$$
Similarly the other way around pushing all to b[j],
$$${c_2 = cost[b[j]] = cd_2 + cd_1 + n_1d}$$$
By pushing elements to p, we get cost[x] i.e.
$$${c_3 = cost[x] = cd_1 + cd_2 + n_1x + n_2(d-x)}$$$
To compare, since all have $$${cd_1 + cd_2}$$$ common, eliminating them, i.e.
$$${c_1 = n_2d}$$$
$$${c_2 = n_1d}$$$
$$${c_3 = (n_1 - n_2)x + n_2d}$$$
Case 1: $$${n_1 = n_2}$$$
Then, $$${c_1 = c_2 = c_3}$$$.
$$${\therefore min(c_1, c_2) = c_3}$$$
Case 2: $$${n_1 > n_2}$$$
$$${c_1 = n_2d < c_2 = n_1d}$$$
$$${c_3 = +zx + n_2d = +zx + c_2}$$$, where z is a positive value = $$${n_1 - n_2}$$$
$$${=> c_3 > c_2 > c_1}$$$
$$${\therefore min(c_1, c_2) = c_1 < c_3}$$$
Case 3: $$${n_1 < n_2}$$$
$$${c_1 = n_2d > c_2 = n1_d}$$$
$$${c_3 = -zx + n_2d}$$$, where z is a positive val = $$${n_2 - n_1}$$$
$$${\therefore c_2, c_3 < c_1}$$$
now taking,
$$${c_3 - c_2 = n_2d - n_1d - zx = (n_2 - n_1)d - zx = zd - zx}$$$
$$${=> c_3 - c_2 = z(d - x)}$$$, but $$${d > x}$$$,
$$${(\therefore c_3 > c_2 => min(c_1, c_2) = c_2 < c_3)}$$$
hence proved.
Therefore, the optimal value will always lie on array elements.