Hi all. I have question. When we mod the hash value of substring, we need prime number, right? Are there some optimal prime numbers so that same hash value of different pattern can be minimized?
Thanks
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
Hi all. I have question. When we mod the hash value of substring, we need prime number, right? Are there some optimal prime numbers so that same hash value of different pattern can be minimized?
Thanks
| Name |
|---|



It would be ideal to keep 2 hash functions. 100007 and 100021 are two good prime numbers to be used.
Ohh nice idea. Thanks a lot
I believe you meant 1e9 + 7 not 100007 because it's divisible by 97. Anyways, you shouldn't use well known prime numbers like 1e9 + 7 (it appears so much in contests that's why it's well known) because the problem setter may set test cases that fail this prime number (and I had it happened to me once when I used 1e9 + 7), you should use a RANDOMLY generated prime number.
Sorry, my mistake. What i wanted to say was 100003 instead of 100007. It' not necessary that you should use randomly generated prime numbers. If you use two hash functions it's very hard to find a case that fails.
Please don't confuse others. According to birthday paradox, you need to generate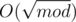 random strings to get two different strings with equal hashes.
random strings to get two different strings with equal hashes.
Even worse: to generate lots of strings with equal hashes it's enough to have only one(!) pair of strings with equal hashes. So this problem remains feasible even for double hashes modulo primes of magnitude greater than 10^9.
If the first function generates numbers uniformly in [0,M1) the probaility for a collision is 1/M1. If you add up another function independent form the first one which returns numbers in [0,M2) the probability of a collision drops to 1/M1 * 1/M2. This is way i said that it is hard to find two stings which fail the test. Am I wrong?
I'll just leave it here.
Generally, the larger the prime number is, the lower is the chance to have two different patterns with the same hash value (this by the way is called collision). Here are some primes easy to remember that guarantee low error probability:
Check this site: http://www.numberempire.com/primenumbers.php
They may guarantee low error probability, but are too large for integer arithmetic (even 64-bit), you'd need bigints to get substring hashes.
One can also use pairs of hashes modulo 2 different primes, though. It's even better since the probability of collisions decreases roughly as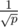 , and what we'd get is basically a hash modulo their product, which is around 1018 if we use primes around 109 (109 + 9, 109 + 7 are good examples), and we can use 64-bit integers freely.
, and what we'd get is basically a hash modulo their product, which is around 1018 if we use primes around 109 (109 + 9, 109 + 7 are good examples), and we can use 64-bit integers freely.