В задаче необходимо было посчитать количество различных букв в множестве. На мой взгляд, самый удобный способ сделать это такой. Переберем все буквы латинского алфавита и проверим, что буква присутствует в строке с помощью встроенных средств языка.
443B - Коля и тандемный повтор
Допишем к заданной строке k знаков вопроса. Переберем все возможные позиции начала и конца тандемного повтора в новой строке. Далее за O(n + k) для каждого варианта узнаем, может ли там находится тандемный повтор. Для этого проверим на равенство нужные пары символов (с учетом того, что знак вопроса равен любому символу).
Понятно, что от порядка, в котором делаются подсказки ничего не зависит. Всего бывает 10 типов подсказок. Переберем все 210 вариантов того, какие подсказки делают другие игроки. Как узнать, сможет ли Боря про каждую свою карту сказать, какого она цвета и что на ней написано. Необходимым и достаточным условием этого является условие, что любые свои две различные карты он сможет отличить. Боря может отличить две карты, если ему подсказали хотя бы про одно отличие. Например, ему подсказали про цвет одной из карт (при условии, что цвет другой карты отличен).
Отсортируем всех друзей по неубыванию их надежности. Если самый надежный друг имеет вероятность 1, то следует попросить только его. Далее будем считать, что у всех друзей вероятность меньше 1. Распишем величину, которую необходимо максимизировать.
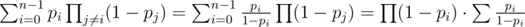
Пусть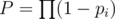 
, а 
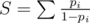. Пусть уже набрана некоторая группа людей, которых нужно попросить. Рассмотрим, как изменится вероятность успеха, если добавить к этой группе друга, который имеет вероятность pi:
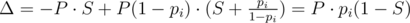
Значит, добавление человека в группу увеличивает вероятность успеха только в случае S < 1. Теперь рассмотрим следующий вопрос. Пусть уже набрана некоторая группа людей, у которой S < 1. Какого из двух людей лучше добавить к этой группе? Пусть вероятность первого человека pi, а второго pj, тогда первого лучше добавить, если:
Δi - Δj = P·pi·(1 - S) - P·pj·(1 - S) = P·(1 - S)·(pi - pj) > 0. Из условия, что хотя бы одного из них выгодно добавить (S < 1) получаем, что pi > pj.
Однако, это только локальный критерий оптимальности. Но, оказывается, что глобально выгодно так же брать только группу людей с самыми большими вероятностями. Докажем это утверждение от противного. Рассмотрим оптимальный ответ, в котором взят как можно больший суффикс (изначально мы отсортировали людей по их вероятностям). Среди таких ответов возьмем тот, в котором меньше всего людей. По предположению так же существует человек, который не входит в ответ, но у которого вероятность больше, чем у одного из тех, кто входит в ответ. Рассмотрим множество людей, которые входят в ответ без этого человека. К нему должно быть выгодно кого-то добавить, так как мы потребовали минимальность количества людей в ответе. Но, из предыдущих выкладок понятно, что добавление человека, у которого pi больше, принесет больше пользы. Значит, пришли к противоречию оптимальности изначального ответа.
Таким образом получаем довольно простое решение. Необходимо перебрать количество людей, которых мы попросим, и всегда брать только самых надежных. Из-за необходимости сортировки получаем сложность решения O(nlogn).
Понятно, что никогда не выгодно удалять крайние элементы. Рассмотрим минимальный элемент массива. Пусть он равен x, а всего в массиве n элементов. Тогда, если вычесть его из всех элементов массива, то ответ уменьшится на (n - 2)·x, так как далее будет совершено n - 2 удаления не крайних элементов, а каждое из удалений принесет на x очков меньше.
Если минимальный элемент был самым крайним, то можно считать, что его совсем нет (так как теперь он равен 0, который никак не влияет на очки). Если же минимальный элемент находился где-то в центре, то утверждается, что оптимально его удалить раньше всего. Докажем это утверждение от противного. Для этого рассмотрим оптимальный ответ, в котором удаление этого элемента стоит раньше всего (но не на первом месте). Докажем, что можно удалить его еще раньше. Если перед ним удалили элемент, который не стоит с ним рядом, то их удаления можно поменять местами. Если же он стоит рядом, то, расписав полученные очки, можно увидеть, что лучше вначале удалить минимальный элемент.
Таким образом, в данной задаче необходимо было поддерживать множество еще не удаленных элементов (и уметь находить соседей), а также находить минимальный из них. Это можно делать встроенным средствами языка за время O(nlogn).
Для начала научимся решать задачу для уже построенного дерева. Это можно сделать с помощью простого динамического программирования. Будем считать ответ для поддерева некоторой вершины плюс ребра, которое ведет в предка. Тогда ответом на задачу будет максимум среди ответов для всех детей корня. Что же такое ответ для некоторого поддерева? Рассмотрим ответы для всех детей. Понятно, что исходящее в родителя ребро нужно покрасить в цвет, который соответствует ребенку с максимальным ответом. Тогда, если два максимальных ответа для детей равны max1 и max2, то ответ для вершины будет max(max1, max2 + 1), если max1 ≥ max2.
Теперь научимся считать ответ для дерева, в котором появляются новые вершины. Для этого воспользуемся тем же самым динамическим программированием. При этом будем пересчитывать ответ только для тех вершин, у которых изменился ответ у детей. Если поддерживать два максимума для каждой вершины за O(1), то утверждается, что все решение будет работать O(nlogn).
Чтобы понять справедливость этой оценки вспомним, что такое Heavy-light decomposion. То, каким образом разбивается дерево на пути при использовании Heavy-light decomposion, является частным случаем этой задачи. Но, про Heavy-light decomposion известно, что ответ (количество различных путей на пути до корня) не больше двоичного логарифма от количества вершин. Значит, каждое из n значений динамического программирования будет увеличиваться не более O(logn) раз.
442E - Гена и второе расстояние
Для решения этой задачи можно воспользоваться двоичным поиском. Что значит, что ответ на задачу не менее R? Это значит, что существует круг с таким радиусом и центром внутри прямоугольника такой, что внутри него находится не более одной точки. Как проверить, что такой круг существует? Его центр всегда можно подвинуть таким образом, чтобы на его границе лежала как минимум одна из заданных точек. Можно перебрать эту точку и проверить, что на окружности радиуса R с центром в этой точке можно найти такую точку, что построив окружность с центром в ней, она покроет не более одной другой точки. А это можно проверить следующим образом. Построим n - 1 круг с центрами в оставшихся точках и пересечем их с данной окружностью. Понятно, что пересечение окружности с кругом будет является некоторым отрезком углов. Необходимо найти такой угол, который покрывается не более чем одним отрезком. Это почти стандартная задача, которая решается за O(klogk), где k — количество точек пересечения.
Мы описали решение, которое работает за O(logAnswer·n2·logn). Однако, его можно еще ускорить. Для этого необходимо вначале перебрать вершину с центром в которой мы строим круг, а потом делать двоичный поиск. При этом не следует делать двоичный поиск, если в данной вершине не достижима текущая лучшая оценка на ответ. Утверждается, что, если точки обрабатывать в случайном порядке, такое решение будет в среднем работать за O(logAnswer·nlog2n + n2logn). Это произойдет из-за того, что двоичный поиск будет вызван приблизительно logn раз. Эта оценка доказывается следующим образом. Рассмотрим вероятность того, что на i-м шаге будет вызван двоичный поиск. Если все числа различны и переставлены случайным образом, вероятность будет равна 
. А как известно сумма первых n членов такого ряда ограничена logn.
В этой задаче есть некоторые технические сложности, которые необходимо учесть при реализации алгоритма. Например, оценка на logn вызовов двоичного поиска справедлива только в случае, если мы ищем строго возрастающую последовательность. Поэтому перед запуском двоичного поиска необходимо проверить достижимость не просто текущего лучшего ответа, а значения, которое немного превышает текущий ответ. Также, необходимо правильно интерпретировать слово "немного" (это должно быть число близкое к eps·curAnswer, где eps — точность, которая требуется в условии).
Также хочется отметить следующий интересный момент в этой задаче. Если написать решение, которое работает за O(logAnswer·n2·logn), то оно будет очень быстро работать на случайных тестах, так как каждую окружность будет пересекать небольшое количество других окружностей.
Что-то я не понимаю, как решение C работает на тесте
1 2 3 4?ans = (2 * 1) + (1 * 1) = 4, удалили 1, остались 1 2 3, удалили 1, остались 1 2.
Amazing speed!!!!!How fast!!!! I think it is the fastest editorial....
Спасибо за разбор, ДИВ1 С, ясно как посчитать ответ, можете ли сказать как его воспроизвести? Т.е. если дан массив, то как удалять элементы, чтобы получить лучший ответ.
Если минимальный элемент оказался крайним, то отложим его удаление на конец, а иначе удалим его прямо сейчас.
и? Как с остальными? На примере 1 2 3 4.
На каждом шаге мы делаем что-то с очередным минимумом, если он где-то в середине, мы его просто удаляем и
ans += min(a, b);где a и b — соседи минимума. Если же он с краю, то мы применяем следующий прием: мы вычтем из всех элементов последовательности значение этого минимума и будем рассматривать ответ для уже новой последовательности, ответ при этом будет на (n — 2) * x больше ответа для новой последовательности.Пусть
ans = 0;В примере первый минимум это 1, применим прием, получим последовательность 0 1 2 3, но к ответу нужно добавлятьans += (4 - 2) * 1. 0 можно отбросить, теперь для последовательности 1 2 3 применим прием: 0 1 2, ноans += (3 - 1) * 1. В последовательности 1 2 оба элемента крайние — ее нет смысла рассматривать.Это написано в разборе, мой вопрос в другом, не как посчитать максимальный ответ, а как воспроизвести его получение.
Мой код: 6931299 Тут немного другой метод чем в разборе, получается если минимум стоит на конце, мы прибавляем к ans его значение и удаляем его. Делается это из следующих соображений, мы решили оставить его удаление на конец, когда оставалось 3 элемента мы удалили средний, получив за это минимум из его окружающих, но наш текущий минимум — это самое маленькое значение на текущий момент, то-есть мы получили как раз наш минимум. Поэтому мы прибавили его к ответу.
where c, d , e editorial for div 2 ??
C,D,E Div2 are A,B,C div1
Can you put a code for them?
В div1C ответ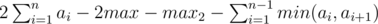
, где max и max2 — первый и второй максимумы.
Уже исправили
Это называется "несложно заметить"
а как это показать не угадувая ответ?
Не очень просто. Попробую объяснить.
Пусть dl, r — ответ для подотрезка массива с l по r включительно. Если на отрезке не больше двух элементов, то dl, r = 0. Иначе, концы удалять никогда не выгодно. Пусть ai — элемент, удаленный на этом отрезке последним, тогда оптимальный результат равен min(al, ar) + dl, i + di, r, отсюда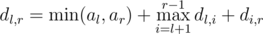
.
Рассмотрим пример: пусть у нас 6 элементов, и на отрезке с 1 по 6 максимум в последнем соотношении достигается при i = 3, тогда ответ равен d1, 6 = min(a1, a6) + d1, 3 + d3, 6. Внутри d1, 3 максимум может быть только при i = 2, и d1, 2 = d2, 3 = 0, поэтому d1, 6 = min(a1, a6) + min(a1, a3) + d3, 6. Пусть на отрезке [3; 6] максимум достигается при i = 4, раскрывая до конца, получим d1, 6 = min(a1, a6) + min(a1, a3) + min(a3, a6) + min(a4, a6). Мы можем видеть, что ответ складывается из слагаемых вида min(al, ar), при этом если такое слагаемое встречается, то в сумме присутствуют слагаемые, максимально "разбивающие" отрезок [l;r] на элементарные отрезки длины не больше 2 (длина здесь — это разность r и l). Для примера "разбиение" схематически выглядит так:
Но это не совсем разбиение; оно станет таковым, если добавить к этой сумме все отрезки длины 1:
По факту слагаемые для отрезков длины 1 не входят в ответ, но мы можем заметить, что каждый такой отрезок ровно один раз входит в любое разбиение, поэтому добавим их туда специально, а потом вычтем из итогового ответа (в исходной записи ответа это последний член).
Теперь будем говорить в терминах построения разбиений. Сделаем так: будем вставлять в массив элементы в порядке убывания и смотреть, как меняется оптимальное разбиение и ответ для него. Для первых двух элементов (максимумов) разбиение состоит из одного отрезка длины 1, и ответ равен второму максимуму.
Вставляем новый элемент ai в существующее разбиение. Если он не является крайним, то его можно удалить первым. Пусть он попал в некоторый элементарный отрезок (концами которого являются элементы, на прошлом шаге бывшие соседними), разбиение изменится следующим образом:
Никаких новых отрезков не появится. Поскольку новый элемент минимален, к ответу прибавится 2ai. Если же новый элемент расположен с краю, то разбиение изменится следующим образом:
т.е. добавится один элементарный отрезок и один отрезок для всего массива. Опять-таки, к ответу прибавилось 2ai.
Видим, что в конечном итоге все элементы учтутся по два раза, кроме максимума, который учтется ноль раз, и второго максимума, который учтется один раз. Это и отражает формула.
Прошу прощения за многобукаф, я пытался повторить ход своих мыслей во время придумывания этой задачи, а не привести максимально простое доказательство. Если вдруг есть вопросы, постараюсь ответить.
Sorry, I chose Russian by mistake.
I like C problem very much. I also like D problem. Thank you for your interesting problems:D
В div. 1 A можно ещё руководствоваться таким критерием допустимости набора подсказок:
Эти условия проще понять, если представить цвета и номера вершинами в двудольном графе, а типы карт — рёбрами между ними. Тогда любая вершина может быть определённой или не определённой. Первое условие означает, что есть не более одного ребра между двумя неопределёнными вершинами во всём графе. Второе означает, что для любой определённой вершины существует не более одной смежной с ней неопределённой.
I'm really impressed with the quality of the problems and the editorial!
Btw, is 442A with the cards and instance of some well known NP-complete problem? First I was thinking set-cover, but that doesn't really fit. Maybe there is some other graph way to formulate it?
Someone please explain Div2 Problem B. :(
Someone please explain Div2 problem B.
Check my solution at : here First add "." k-times after input string and bruteforce find optimal start character of tandem and length of it in new string.
For problem E you can also use Voronoi diagrams.
1) Build the diagram of the whole set, call it V
2) For each point p, build the diagram of its neighbors in V, call it N.
3) Use the vertices of N as candidate solutions.
In step 2) we're looking at what happens when p is the closest point, and it's easy to see that the optimal point in that case has to be one of the vertices of N (since they are the most distant from surrounding points).
Since the number of points is not too big, you can use the simple half-plane intersection algorithm to find a Voronoi cell in O(n log n), and the whole diagram in O(n^2 log n).
It's crucial to look only at the neighboring points of p in step 2 (looking at the diagram of all points except p would also be correct, but slow), as otherwise you'll be recomputing the whole diagram n times. This way the complexity of the whole thing is still O(n^2 log n) (if I'm not mistaken).
can you provide me some links to this simple voronoi building algorithm? All I could find in my researches was an O(n^4) algorithm and the reaaally big O(n log n) sweep line one.
EDIT: nvm, when I searched for "O(N^2 log(N)) voronoi" this popped out: http://web.mit.edu/~ecprice/acm/acm08/notebook.html#file7
C can also be solved in O(n):
While there are elements ai such that ai - 1 ≥ ai and ai ≤ ai + 1, we always want to remove ai before removing ai - 1 or ai + 1. (When doing the comparisons, we assume a0 = an + 1 = 0.) We can maintain a queue of elements with this property, and delete those elements. After removing an element, we check if we need to push one of its neighbors onto the queue. Once there are no more elements like this, we have a bitonic sequence, which is easy to deal with.
My code implementing this algorithm is here.
I don't know how I solved D(div 1. B) but I didn't realise how to solve B nor C... Kind of weird.
Same here! It's weird, it seemed like easy elementary school probability math. Although div2b was really easy, I just forgot that one if-clause there.
D wasn't that obvious to me, lol and i've never seen this kind of probability problem in elementary school, unfortunately. B was way easier, but I was afraid of being hacked from the moment i send it (didn't bother to check for corner cases)
Can u ans(ans explain) for test case Q.4(Div 2)
3
0.087234 0.075148 0.033833
first sort the probabilities.. then suppose they are a,b,c in sorted order 1.Take a*(1-b)*(1-c)+b*(1-a)*(1-c)+c*(1-b)*(1-a) which is prob of getting one of them at a time. 2.Then leave the smallest probability a,then find b*(1-c)+c*(1-b) 3.Then leave prob b and take c. 4.Take the best value(closest to one) among the three calculated above. Using this u can calculate the answer for ur test case.
I think it is better to include a standard solution link after each problem's editorial.
Exactly! I just don't understand the explanation for problem B div2 :(
I hope this helps!
Thanks a lot! I see that your algorithm is as same as thee editorial. I'm understanding it better.
I didn't understood how to solve 443B can someone explain how to solve with example.
my explanation based on the editorial:
?k times to the end of string to get a new string. Lets call its.j=length(s) div 2.i=1.copy(s,i,2*j). Let divide the substring into 2 strings:string x=copy(s,i,j)andstring y=copy(s,i+j,j).xandy, we replace every?in stringywith the character in respective position of stringx. After the replacement, ifx=ythen we have a tandem string; if not, increaseiby1and go back to Step 4.i>(length(s)-2*j+1)and we cannot find tandem substring with length2*jwe decreasejby1and go back to Step 3.my code: 6926507
sorry for my limited english :)
Nice Competition
@ m3kAnix
Explanation of problem (div2)B: Let's see an example. The input string is "abc" and the value of k is 5. Now we have to check all possible string for tandem repeat. New length of the string is 3+5=8. so let's assume our new string "abc?????" now when we check for tandem repeat and we encounter position 1 and position 4 we get 'a' and '?' .We take that as a match. if we encounter 'b' and '?' then we also take that as a match. '?' can be any character, that's the point.
Div 2, Q 4
Getting WA on test case 12 i.e
3
0.087234 0.075148 0.033833
According to me, ans should be 0.149271078736(taking first 2 elements together) but its 0.172781711023(according to judge)
Any suggestion plz ??
if in your last sumbission you change line
to
It will get AC.
Got my mistake Thanks a lot...!!!
I don't get div2 E (div1 C) explanation. It states that we need to choose the minimal alive element, excluding the borders, but test case 3 already shows it's not true. Deleting minimal elements first results in the answer "3". Am I missing something?
I also did not get it either.
But from this solution what I get is, at first I've to choose
Aisuch thatAi-1 >= Ai <= Ai+1Then we sort the remaining and choose all except bigger two of them, as we have to take minimum value.how do u type
(with subscript) within the
Inline?I use HTML < sub > tag.
subtag
test:
sumi = sumi-1 + aithanks, i figured it out. :)
This solution implements the idea described in the tutorial. I'm still working to understand it.
Thanks. Now I understand the tutorial. This is exaclty the described solution.
I will try to explain here.
Now,Lets see. There can be repeated elements. Like 3 can be in many positions. So to identify each appearance we need a touple like (value,pos) or (pos,value) . Each touple will be unique.
We consider (val,pos) in increasing order.[As explained in the editorial. This is a simple proof by contradaction. I can explain it further if needed.]
The main loop runs for (n-2) times. In each iteration it edits the ans by (val-cero)*(n-i-2). Here cero is SO FAR seen lowest VAL. And (n-i-2) is its contribution.
I tried to put as much detail as possible in this submission. Hope it helps :)
14996334
Agreed, i also find this as wrong solution (or maybe i just dont understand something ?). I could say it would work if removing something at the first or last place of an array would give points for its only neighbour, but we get nothing so it's actually wrong solution.
Can someone explain why "Boris can describe all of his cards iff he can distinguish all pairs of different cards" (Div1 A/Div2 C)?
I don't have idea why the grader and custom output different. Could someone help me on this?
Submission : 6930710
i didn't understand problem C div 2 at all, can anyone please help me to understand how to solve this problems?
Thanks :)
Basically you can try every combination of hints. There are 2^10 = 1024 combinations. (Note that the order does not matter.)
D: In fact, the asymptotic run-time of each operation is O(1); there are at most N nodes with DP value at least 1, N/2 with DP value at least 2, ..., 1 node with DP value at least log(N), so the sum is 2N, not N log N.
Not true. Consider the following tree:
Simple path of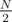
nodes:
And full binary tree of size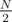
rooted at vertex (N / 2).
Here the DP values of the first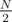
nodes will be 
.
you are right. my bad.
Would anyone please discuss the solution with an example of 442A - Borya and Hanabi ? I am finding
"He can do it iff he can distinguish all pairs of different cards. He can do it if somebody told at least one distinction. It can be a hint about color of one of cards (if they don't have same one) or it can be hint about value of some card."
this portion hard to understand. Any help would be appreciated.
He can only distinguish two cards (say A and B) if there was a hint that was applicable to A but not to B or the other way round.
Now when you start brute forcing through all possible sets of hints, for every set of hints see which card gets pointed at by which hint. If for two different cards the hints that pointed towards them are different only then can he tell that the cards are different otherwise he can't and that particular set of hints is not enough to tell all cards apart.
What about if there are multiple cards of same colour and value? Would you mind clarifying it ?
INPUT :
3G4 G4 G4 A5If you can distinguish one G4 from A5 then you can distinguish all G4's from A5. Let me try an example: if you're currently testing whether the set of hints {G,2,3} works or not then
1st G4 is pointed at by hint {G}
2nd G4 is pointed at by hint {G}
3rd G4 is pointed at by hint {G}
A5 is not pointed at by any hint among {G,2,3} therefore {}
Now, using the hints that each card is pointed at, you can distinguish between the first three cards and the fourth one as they have different sets of hints pointing at them. You cannot however distinguish between the first three cards. Now if the first three cards are equal then this condition is fine as any hint that points at card 1 will also point at the other two. However, if the first three cards are different then we have a problem.
let us try out the set of hints {1,2,3} for G1 G1 R1 R2
pointing at card 1 {1}
card 2 {1}
card 3 {1}
card 4 {2}
We can tell apart the 4th card from the others but we can't distinguish between the first three cards. As the first three cards are not the same, therefore, this set of hints is not enough to determine each card.
Can someone please explain the 5th test case in problem B DIV2
The tandem repeat would be like this :
ayiabc ayiabc aMaximum length is 12. So the answer is 12.
Can someone please explain Div2 E (Div1 C) explanation? It says choose the minimum alive element. But following this in test case 3 (1 2 3 4 5), we get a wrong answer = 3.
can anybody explain the solution of problem E div 1.
This solution for E is very interesting. Can anyone explain me in which kind of situations is this random walk applicable ?
Can anyone explain me in detail How to solve Borya and Hanabi using BitMasking or Is their any other approach to solve this problem. Thank You In Advance !!
start with the bitmask = 0 and add one to it until it reaches 2^10-1, that means you'll have all bitmasks from 000000000 to 111111111, which are all the different combinations of tips (first bit to fifth: tips for indexes (1, 2, 3, 4, 5); sixth to tenth: tips for letters (R,G,B,Y,W)).
now, all you have to do is check if the tips you have on (bit on bitmask = 1) are enough in each iteration and get the minimum number of "on" bits. you can check if the tips are enough by just comparing each card to each other. There are 3 types of pairs of cards: 1) Different Indexes (1R and 2R) You need a tip for either index 1 or index 2 (tips for colors are not important) 2) Different Colors (1R and 1B) You need a tip for either color R or color B (tips for indexes are not important) 3) Different Indexes and Different colors (1R and 2B) You either need a tip for 1, 2, R or B (only one is enough) 4) Cards are the same (1R and 1R) You don't need any tips
If you have a valid tip for each pair of cards, then the bitmask is a valid choice of tips, and you can make ans = min(ans, number of 1 bits in bitmask)
Okaye . . Now I got it .. Thanks for this great explanation .. @caioaao
You're welcome! I know how frustrating it can be when we don't understand an old editorial and there's no one there to answer your doubts, so I'm glad I could help :D
Yups Bro. . I totally agree with you. It happens when you are in learning phase and Sometimes we unable to understand the editorial as well as other Coder's code . btw this time I'm lucky that you helped me. :-)
thanks for this great explanation :)
Can anyone explain me in detail How to solve div 1 problem C Artem and Array? thanks in advance.
443A I solved it by iterating the given string and set elements in array of ints equal to size of English letters, and finally sum all the 1s in the array. I guess its of O(n + k) where k = 26, and for n >> k, its O(n). The solution refered to here will cost more than that as I will iterate over the string 26 times O ( k * n ).
As n is smaller than 1000 and k is 26, the difference between O(k * n) and O(k + n) isn't very big and both solutions work very fast. I described solution which in my opinion is easier to code.
Hi isn't problem E Gena and Second Distance a typical denaulay trianglution problem? find denaulay trianglution of N points and compute the maximum circumradius of each denalay triangles?
As you correctly mentioned in russian-language thread n*log(n) delaunay triangulation is not very easy thing, and it's hard to write it during the competition (but you can solve this task with some modification of it). The solution I described in the editorial can be written in just 20-30 minutes.
I moved from Topcoder to practice here as the quality of their tutorials drastically go down after SRM 600.
I started with CF 253 and problem C. What's this shit???? I don't understand even a single word of this fucking tutorial. There are lots of grammatical mistakes and typos with no proof!