I always see problems that need to print the result of C(n,m) mod a prime number where C(n,m) = n!/(m!*(n-m)!) the factorial formula of binomial coefficients. I've searched for it and I found that I need to find the multiplicative inverse using extended Euclidean algorithm and I've learnt it. I hope if somebody could tell me the fastest way to find C(n,m) mod P (P is a prime) using extended Euclidean algorithm and I would be thankful if there was a code. Thanks a lot.
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | adamant | 152 |
| 6 | djm03178 | 152 |
| 8 | Qingyu | 151 |
| 9 | luogu_official | 149 |
| 10 | awoo | 147 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/21/2025 00:34:06 (k2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










I don't know how to " find C(n,m) mod P (P is a prime) using extended Euclidean algorithm". But, this is the way i use to find C(n,m) mod P : - If n is small (~10^4), you can caculate C(n,m) mod p with a simple O(n^2) dynamic programming. - With bigger n, you can see problem Super Sum on this lịnk. Author used Fermat Little Theorem to calculate inverse modulo p of denominator in C(n,m).
Hope it's useful.
There is also a solution with extended Euclidean algorithm. You can find more about it on e-maxx (Russian).
But it looks like solution with Euler's Theorem is easier. We know that
So,
Or for prime m
Try this.
Thanks it too useful
if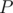 is a prime, then
is a prime, then 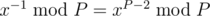 .
.
so u can use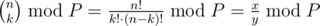 (say)
(say) 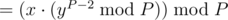
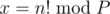 and
and 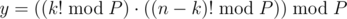
in above formula,
thanks it is clear now
It's all about the Fermat's little theorem.. Efficient time complexity would be O(k*log(p)) which is much better