Недавно я с удивлением узнал, что алгоритм, которым я пользовался для нахождения минимального пути в графе от одной вершины до остальных, не совпадает с классической дейстрой описанной на википедии или e-maxx. Теперь напишу, как я ищу минимальный путь.
- Создаем линейный массив cost в котором будем хранить минимальное расстояние до каждой вершины. Инициализируем его БОЛЬШИМИ значениями, а для стартовой вершины запишем 0.
- Создаем сет интов s, в него мы будем помещать вершины, которые стоит посетить. Изначально s содержит только стартовую вершину.
- Пока s не пустой выполняем следующее
- берем вершину с начала s, обозначим ее через u, удаляем из сета;
- проходимся по всем ребрам идущим из u. Пусть текущее ребро соединяет вершину u с вершиной v и имеет вес w. Если cost[u]+w < cost[v] тогда обновляем значение для cost[v]= cost[u]+w и добавляем в s вершину v, так как мы нашли до нее "более короткий" путь.
В массиве cost содержаться минимальные расстояния до каждой вершины.
код:
const int inf= INT_MAX/2;
const int MaxN= 2000;
vector<pii> a[MaxN+5]; // список смежности.
//a[i][j].vartex – номер вершины смежной с i-ой,
//a[i][j].weight – вес ребра, соединяющего эти вершины.
int cost[MaxN+5];
...
int u,w;
int from; //номер стартовой вершины.
// заполняем массив БОЛЬШИМИ значениями
for (int i=0; i<=MaxN; i++)
cost[i]= inf;
set<int> s;
s.clear();
// кладем в начало сета "стартовую вершину" и ставим расстояние до нее 0
s.insert(from); cost[from]= 0;
int c;
while (!s.empty()) //пока сет не пустой
{
u= *s.begin(); c= cost[u];
s.erase(s.begin());
for (int i=a[u].size()-1; i>=0; i--)
{// проходимся по всем вершинам смежным с u
if (cost[a[u][i].vartex]>c+a[u][i].weight)
{// если до текущей вершины путь через u "короче"
cost[a[u][i].vartex]= c+a[u][i].weight; // обновляем значение в массиве
s.insert(a[u][i].vartex); // добавляем в сет
}
}
}
Я пока что точно не оценил сложность алгоритма, но надеюсь на что-то вроде O(E logV), где V – количество вершин, а E – количество ребер в графе. Из возможных преимуществ данного алгоритма можно считать: чуть более краткий код, корректность работы при отрицательном весе ребер.
И собственно вопрос)) можно ли этот алгоритм считать модификацией Дейкстры или он как-то по-другому называется? Или это вообще не ясно что?))
UPD Как уже написали хорошие люди, этот алгоритм неэффективный. так что лучше им не пользововаться











Про эту модификацию алгоритма Дейкстры писали тут : http://codeforces.net/blog/entry/3793
Спасибо, интересно почитать. Но я еще не понял, что такого плохого в тесте из ссылки и соответственно "лечится" ли это тем, что брать не с корня, а случайный элемент.
Так а что меняет то, что мы берем случайный элемент?. Я почти уверен, что будет еще хуже.
Эту реализацию можно считать модификацией алгоритма Дейкстры, но работающую за O (VE); например на таком тесте: 5 — число вершин 10 — число рёбер. Из какой вершины идёт ребро — 5, в какую вершину идёт ребро — 1, вес — 10 (далее — аналогично); 5 2 6; 5 3 4; 5 4 2; 2 1 1; 3 2 1; 3 1 1; 4 3 1; 4 2 1; 4 1 1; from = 5
В посте, который я привел выше, говорится, что данный алгоритм на графе с отрицательными ребрами, работает за экспоненциальное время.
UPD: Тут чушь была написана.
на данном тесте алгоритм выполняется за 11 добавлений в сет. если я правильно "понял" граф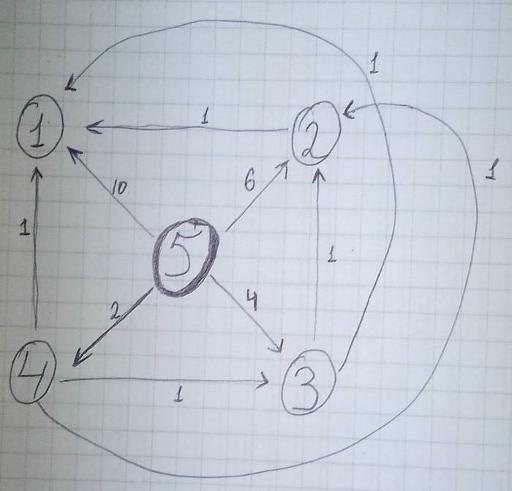
UPD: и при каждом добавлении проходимся по всем ребрам и выходит много..
спасибо за тест))
Я думаю, её всё же нельзя считать модификацией Дейкстры, так как в Дейкстре вершины посещаются в порядке увеличения расстояния до них. Здесь они почему-то посещаются в порядке, кхм, увеличения номеров, так что это модификация алгоритма Левита.
Я что-то не так сказал? :)
Ой, а я и не заметил, что он не смотрит на расстояние до вершины, а на номер вершины.
UPD: не увидел, что
setвообще не учитывает расстояние до вершин и выбирает минимальную по номеру.Это вообще квадрат числа рёбер. Тест:
Вы сначала добавите в сет вершины 1... n, затем из каждой из них добавите B, а потом пройдётесь из B по всем исходящим рёбрам — итого квадрат.
Надо проверять, что вы раньше не обрабатывали исходящие рёбра из этой вершины (и перебирать рёбра из каждой вершины только один раз) — тогда получится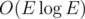 .
.
Если еще и не хранить несколько значений для одной вершины в сете —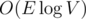 .
.
А если вместо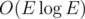 , который работает очень быстро.
, который работает очень быстро.
setиспользоватьpriority_queue, то будетспасибо!
ко мне можно на ты обращаться))
в данном тесте, если номер В больше N тогда мы из В запустимся только 1 раз и выдет O(E), если же номер В — 0, тогда да, очень плохо... и тут появляется вопрос брать ли с корня и со случайную вершину, но в принципе понятно, что алгоритм не надежный))
интересно, что я уже почти 4 года нахожу так кратчайшие расстояния и пока не попадал на ТЛ)) сейчас затестил (100 000 случайных тестов) для полного графа из 100 вершин. Вышло, что в среднем заходим в 350 вершин, максимум в 950. ну а количество действий соответственно в 100 раз больше. таким образом выходит хуже чем O(V*V) даже в среднем... если брать случайную вершину, а не из корня у меня вышло 258 в среднем и 588 в худшем. так что лучше вообще больше не буду так писать)) теперь не понимаю, как он заходил))
А, у вас совсем чушь написана: вообще на расстояние не смотрите в
set. Извиняюсь, невнимательно прочитал.Тогда правда — то, что написано выше. У вас посещаются в порядке уменьшения номеров. И, да, это скорее похоже на то, что называется на e-maxx Левитом и работает за экспоненту. Не уверен, что тот же самый тест подойдёт и сюда.
Это вообще O(2n * n) даже для положительных ребер. Между вершинами i<j проведем ребро стоимости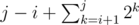 и запустим поиск кратчайшего пути из вершины с номером n-1. Для такого графа каждая вершина попадет в очередь 2n - 1 - i раз.
и запустим поиск кратчайшего пути из вершины с номером n-1. Для такого графа каждая вершина попадет в очередь 2n - 1 - i раз.