Задача A. Предполагалось решение за O(n2).
Получаем фразу парсим её и помечаем те которые явно не походят за O(n). В конце проходим по массиву и считаем количество непомеченных ячеек. Если их 0 - то надо вывести "-1", иначе вывести их количество.
Быстрейший успешный сабмит - 0:02.
P.S.: Кто знает, кто такой Cerialguy?
Задача B. Предполагалось решение за O(k × n × m).
Просто запускаем BFS из нашей точки и обходим всё. Ходим из клеточки по всем направлениям, которых 6. Ответом на задачу будет просто количество посещёных клеток.
Быстреший успешный сабмит - 0:08.
P.S.: Решение усложнялось запутанным условием. :-)!
Задача C. Предполагалось решение за O(27 × n2).
Заметим, что в компоненте связности по одному числу все остальные числа восстанавливаются однозначно, т.к. в каждой паре мы знаем минимальную и максимальную степень простого. Т.к. количество простых в разложении числа " < = 1000000" не больше 7, то мы можем перебрать соответствующие степени - и для каждого полученного числа проверить, что всё сходится.
Как проверять? Для этого нужно заметить, что если мы знаем a, (a, b), [a, b], то 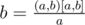 , а потом пройтись и проверить, что всё сошлось.
, а потом пройтись и проверить, что всё сошлось.
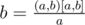 , а потом пройтись и проверить, что всё сошлось.
, а потом пройтись и проверить, что всё сошлось.Быстрейший успешный сабмит - 0:23.
P.S.: Решение с помощью 2-SAT забыл. А в этом, надеюсь, не налажал. :-)!
Задача D. Предполагалось решение за O(величина максимального числа).
Нужно было заметить, что каждая красивая тройка представляется в виде (x2 - y2, 2xy, x2 + y2). Такое вот замечательное свойство у этих чисел. Теперь. Давайте переберём все тройки. Перебирая, мы смотрим - если есть такие числа у нас, а если хотя бы 2 таких таких числа, то их объединяем.
Как перебирать тройки?
x > y.
Заметим, что 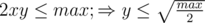 . А, значит,
. А, значит, 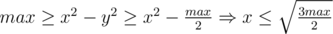 .
.
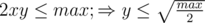 . А, значит,
. А, значит, 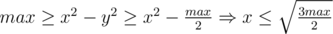 .
.Итого, чтобы перебрать все тройки нам хватит 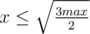 и
и 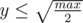 . Количество итераций -
. Количество итераций - 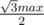 .
.
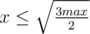 и
и 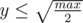 . Количество итераций -
. Количество итераций - 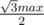 .
.Что означает объединить?
Заводим структуру СНМ - и если 2 числа принадлежат одной красивой тройке, то они соединены ребром, в нашём случае нам достаточно объединить соответствующие им множества.
Быстрейший успешный сабмит - 00:37.
P.S.: Ограничения на задачу были немного уменьшены, в связи с тем, что у меня программа на "Java" долго считывала 107 элементов. И ещё эта задача изначально была рассчитана на Гену, чтобы он не решил! :-)! Просто мне казалось, что не настолько такие факты известны программистам. Извините, если кого-то обидел. Это писалось с моей математической точки зрения. ИЗВИНЯЮСЬ ПЕРЕД ВСЕМИ.
Задача E. Предполагалось решение за O(n + log(xy)).
Нужно было заметить, что сумма спустя 1 минуту изменяется следующим образом - умножается на 3, и вычитаются крайние элементы последовательности. Поэтому сумму можно считать просто быстрым возведением матрицы в степень.
Что происходит после сортировки?
Минимальное число, т.е. первое остаётся на своём месте. А на последнее место переходит число Fxan + Fx - 1an - 1. Где n - количество элементов, а Fx - x-ое число Фибоначчи - при задании F - 1 = 0 и F0 = 1.
Т.е. крайнее число тоже можно было посчитать быстро с помощью быстрого возведения матрицы в степень.
А потом ещё раз применяется первая идея.
Быстрейший успешный сабмит - 00:45.
P.S.: Задача была частично позаимствована с математической олимпиады 4 класса для поступления в кружок при ФМЛ №239. Она была усовершенствована и усложнена.
Я знаю, что разбор не ясен. Поэтому скажите мне - что прояснить.
P.S.: Спасибо всем, кто устранял все баги во время контеста...











о_О 6?
> Я знаю, что разбор не ясен.
Ну зачем так? :-) Вроде основные идеи вполне ясны.
По-моему те кто считают что bfs сложнее просто не умеют его готовить ;)
Ну, или пишут на паскале %)
И стоит ли говорить, что на данный момент самое короткое не питоновое решение - DFS.
Впрочем это всё дело вкуса.
Есть люди, которым естественнее увидеть BFS, например Melamori. А некоторые мыслят рекурсивно и им проще написать более короткий DFS. ;)
Оффтоп.
Интересно, что не было ни одного успешного взлома по задаче В.
To get the sum quickly, what I did was this:
Let the array be S with elements from 1 to N. Let f(x) be the sum of all elements after k moves.
Then f(x) = 3*f(x) - (S[1] + S[N]); f(0) = sum, where sum == summation of all elements in S.
The solution to this recursion is sum * 3^X - (S[1] + S[N]) * (3^X - 1) / 2
However, I have division by 2, and division with modulo seems very tricky to handle. May I know how you solve this issue?
Thanks!
(x2 - y2, 2xy, x2 + y2)
Надо чтоб они были попарно взаимно простые.
Для каких x, y это условие выполняется?
Или это надо для каждой пары потом проверять?
Сложность такой проверки O(sqrt(max))?
How can problem B be solved using DSU. I see DSU tag over there.
Hmm, I think perhaps you mean DSU=Disjoint Set, while I usually call it Union-Find...
I solved this problem by using BFS, but I think as union-find can be used to find out the connected components, I guess that it is used there to find out all the '.' positions that can be reached from the initial position. Nevertheless, I think it is a little weird to use union-find there, since as far as I consider, union-find usually appears with a sparse graph that is described with connected edges, while it seems straightforward to use BFS in this problem...