Problem A. Solution - O(n2).
We take phrase and parse it. Mark all cells, that obviously didn't match - O(n). In the end we go through the array and count all unmarked cells.
If 0 - we print "-1", else - amount of unmarked cells.
Problem B. Solution - O(k × n × m).
We start BFS from given point. Go from cell to all 6 directions. The answer - number of visited cells.
Problem C. Solution - O(27 × n2).
We can see, that in connected component - if we know 1 number - then we know all others in component, because in each pare we know minimal and maximal
power of each primes. Because number of different primes in one number " < = 1000000" is less, than 7, we can look over all possibilities of 1 number in connected compoment - and for each number, that we get, we check, that it suits.
How to check? We can notice, that if we know a, (a, b), [a, b], then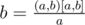 
, start DFS and check.
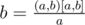, start DFS and check.Problem D. Solution - O(max numebr).
We can notice, that each beautiful triplet has form - (x2 - y2, 2xy, x2 + y2). Now we can gen all such triples. For each triple, we watch - if we have more than 1 number in given set - we union them.
How to gen all the triples?
x > y.
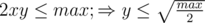. This means, that 
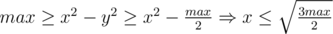.Now for gen all this triples we an take -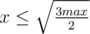 
и 
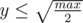. The number of iterations - 
.
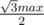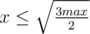и 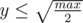. The number of iterations - 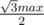.what means - "union"?
We take a data structure named DSU. If two number belong to one beautiful triple - they are connected with edge, in our situation - we can union corresponding to them unions.
Problem E. Solution - O(n + log(xy)).
We can see, that after one minute the sum changes - it multiply on 3, and substract first and last elements of sequence. Because of that we can count of sum with help of power of matrix.
What happens after sorting.
First number stay on his place. On the last place - Fxan + Fx - 1an - 1. Where n - number of elements, ans Fx - x Fibonacci number - with F - 1 = 0 and F0 = 1.
This means - that we can count the last number with matrix too.
After that we use the first idea.
If you have questions - ask them.
To get the sum quickly, what I did was this:
Let the array be S with elements from 1 to N. Let f(x) be the sum of all elements after k moves.
Then f(x) = 3*f(x) - (S[1] + S[N]); f(0) = sum, where sum == summation of all elements in S.
The solution to this recursion is sum * 3^X - (S[1] + S[N]) * (3^X - 1) / 2
However, I have division by 2, and division with modulo seems very tricky to handle. May I know how you solve this issue?
Thanks!
How can problem B be solved using DSU. I see DSU tag over there.
Hmm, I think perhaps you mean DSU=Disjoint Set, while I usually call it Union-Find...
I solved this problem by using BFS, but I think as union-find can be used to find out the connected components, I guess that it is used there to find out all the '.' positions that can be reached from the initial position. Nevertheless, I think it is a little weird to use union-find there, since as far as I consider, union-find usually appears with a sparse graph that is described with connected edges, while it seems straightforward to use BFS in this problem...