Problem : Link
It's a game.Let’s say at the beginning of round i, Alice has a Taka (Currency of Bangladesh) and Bob has b Taka. and c is the minimum of a and b. Alice and Bob are equally likely to win the round. If Alice wins, she gets c Taka from Bob, otherwise Bob gets c Taka from her and go to the next round and so on. Game ends when one of them has 0(Zero) Taka and obviously the person with 0 taka loses.
The initial amount Alice has is a and the initial amount that Bob has is b, you have to find the probability that Alice is going to win and expected number of rounds the game is played.
My solution Idea: There are a situation when playing rounds , we found same position of (a,b) as started .This situation will come when min(a,b) will win the round.Every round the probability to win the round 0.5.
But my solution didn't work ,but why ?
Can anyone explain how to solution ?











EDIT: ignore. this approach won't work because there could be cycles.
you can Use Gaussian Elimination for this problem. first construct the linear equations by finding the dependencies between the states. then Use Gaussian Elimination to find out the answer.
How to find dependencies between the states ? Can u explain ur solution ?
As number of states is not that big. You can generate all the states. Check my AC code : Code
Let's say that the current state of the game is (a,b) ... We have two choices each with probability 50% ... either the player with the minimum number loses, so the game will end ... or the player with the maximum number loses so we will move to another state.
Now it's obvious that the total number of states is a+b ... and from each one of them I'll either end the game, or move to another "unique" state ... So unless a==b, there will always be a cycle.
First we need to find the length of this cycle and then we can state our recurrence relation.
From every state (x,y) ... Let's mark the next state in the cycle as Next[(x,y)] Also let's mark the initial node as (a0,b0) and next one as (a1,b1) and so on.
Then we can say that:
Ans[(x,y)] = 0.5*(x>y) + 0.5*Ans[Next[(x,y)]]Let the length of the cycle be c ... Then we will have c relations of that form ... By substitution we can see that the answer will be of this form
Ans[(a0,b0)] * (1 - (0.5^c)) = 0.5*(a0>b0) + 0.5*0.5*(a1>b1) + 0.5*0.5*0.5*(a2>b2) + ..We can easily get
Ans[(a0,b0)]which is the required outputI only discussed the solution of the second requirement ... I guess the first one can be done in the same manner.
Nope; (3, 1) yields (2, 2) which ends the game, so there's no cycle.
I'm pretty sure the answers are as follows:
The problem is that I haven't managed to prove rigorously those answers.
Can you explain why this solution works ?
i've managed to prove that there won't be a cycle if and only if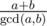 is a power of
is a power of 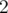 (same condition as urs above).
(same condition as urs above).
my proof uses the fact that in every turn, the player either loses the game completely, or doubles up on the money that he/she had before that turn.
is this enough to complete ur proof? if so, can u tell us how u prove it?
Yes, I have that result too.
So I think I have the proofs. Here, assume Alice and Bob have gold coins instead of Takas. I play too much board games.
First problem:
First, suppose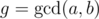 . Then both players will always win/lose coins in the multiple of g, and thus we can state a new unit of currency, let's say diamonds, which worth g gold coins each, and exchange Alice's and Bob's wealth with these. Now the GCD of the number of diamonds they have is 1.
. Then both players will always win/lose coins in the multiple of g, and thus we can state a new unit of currency, let's say diamonds, which worth g gold coins each, and exchange Alice's and Bob's wealth with these. Now the GCD of the number of diamonds they have is 1.
Next, note that if an odd integer k doesn't divide both Alice's diamonds and Bob's diamonds, it will never divide both on the course of the game play (except probably at the end). To see this, suppose Alice wins, and suppose Alice has less diamonds (so the game continues). If Alice's number of diamonds, a, is not divisible by k, then Alice gains the same number of diamonds, so her wealth is now 2a. But since k is odd, this new factor 2 won't help 2a to be divisible by k. If a is divisible by k, then by assumption, Bob's number of diamonds, b, is not divisible by k. But then he loses a diamonds, which is divisible by k, and thus b - a won't be divisible by k.
Lastly, if both balances are odd, then whichever wins will cause both balances to be even. Now similar to when we treat the GCD, we exchange Alice's and Bob's diamonds into super-diamonds, worth 2 diamonds each. This cuts down the number of objects in play by half. It can be proven that not both of them have an even number of super-diamonds, otherwise they would have had an even number of diamonds before this round.
So we can see: as long as both balances are odd, we keep cutting down the total number of objects by half. At the moment this is not the case, then the total number of objects is odd (one has odd and the other even), and by our lemma with the odd numbers, the two balances will never be both divisible by some integer other than 1 before the game ends. Let there be a, b objects held by Alice, Bob respectively; this guarantees that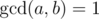 during the game.
during the game.
There's one other case, where all balances will always be odd. Since we keep reducing the total, at some point the total will eventually be 2, which means Alice and Bob are tied and this is the last round.
Now, suppose c = a + b. Then we can see that Alice holds a objects and Bob holds c - a objects. After a round (that doesn't end the game), we can verify that Alice now holds objects and Bob holds
objects and Bob holds 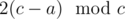 objects; just divide into cases. This means after k rounds, Alice holds
objects; just divide into cases. This means after k rounds, Alice holds 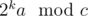 objects. Since c is an odd number, by Euler's theorem there exists some p such that
objects. Since c is an odd number, by Euler's theorem there exists some p such that 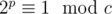 , and thus after p rounds we will arrive back on the same state.
, and thus after p rounds we will arrive back on the same state.
Now, suppose that the number of times we replaced a (super)i - diamond into (super)i + 1 - diamond is k times. Then the probability of arriving here is 2 - k, and the expected number of rounds is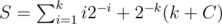 where C is the expected number of rounds from this point. We simplify this first:
where C is the expected number of rounds from this point. We simplify this first:
S = C2 - k + 2 - 2 - k + 1
Now there are two cases:
Alice and Bob are tied. Then this last round ends the whole thing, and thus C = 1. This gives C = 1 and thus S = 2 - 2 - k, as expected.
Alice and Bob are not tied, and thus will never tie. By our assumption above, suppose that there are p rounds such that the state of their wealth returns back to this point. The expected number of rounds is similar to the one for S: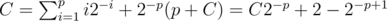 . In other words, C(1 - 2 - p) = 2(1 - 2 - p), and thus C = 2. Plugging back into the formula for S gives S = 2 - k + 1 + 2 - 2 - k + 1 = 2.
. In other words, C(1 - 2 - p) = 2(1 - 2 - p), and thus C = 2. Plugging back into the formula for S gives S = 2 - k + 1 + 2 - 2 - k + 1 = 2.
Second problem in a new comment.
Second problem. You are strongly encouraged to read about super-diamonds in the solution for the first problem first. And yes, simplify gold coins into diamonds; screw those sparkling gold.
First, if a + b is a power of 2, then our game will halt. At all times a, b will always be both odd until the end of the game. Computing the probability of winning is thus simpler; we can use induction on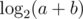 . In case a + b = 21, it's clear that a = b = 1, otherwise we have no game. It's also clear that the probability of winning is exactly half.
. In case a + b = 21, it's clear that a = b = 1, otherwise we have no game. It's also clear that the probability of winning is exactly half.
Suppose that for a + b = 2k, we have proven that the probability of winning for Alice is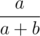 . Take a step up; suppose that our balances are a', b' in diamonds, where a' + b' = 2k + 1. If either is even, then both must be, and thus replace them with super-diamonds to get 2k objects and invoke the induction hypothesis. Now suppose a', b' are odd. Clearly they cannot be equal.
. Take a step up; suppose that our balances are a', b' in diamonds, where a' + b' = 2k + 1. If either is even, then both must be, and thus replace them with super-diamonds to get 2k objects and invoke the induction hypothesis. Now suppose a', b' are odd. Clearly they cannot be equal.
Suppose that Alice is losing. (If Alice is winning, look at Bob instead; Alice's probability of winning is then one minus Bob's.) In half of the case, she zeroes out, and thus loses. In the other half of the case, her balance is now 2a', an even number, and Bob's is b' - a', which must necessarily be an even number (because their sum is even). Thus we can now simplify this one, letting a = a' and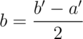 , to get a + b = 2k, and invoke the induction hypothesis to show that Alice has a probability of
, to get a + b = 2k, and invoke the induction hypothesis to show that Alice has a probability of 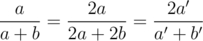 of winning. This occurs in half of the case, so Alice's probability of winning must be
of winning. This occurs in half of the case, so Alice's probability of winning must be 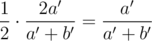 , exactly as our induction hypothesis says. Thus we're done.
, exactly as our induction hypothesis says. Thus we're done.
Now suppose that this is not the case. Suppose Alice's balance is a and Bob's is b, where both have opposite parities. Then by the lemma proven in the solution for the first problem, after several rounds, say k, we will return back at this exact state. Let the probability for Alice to win, given balance a with a fixed sum c = a + b, be P(a).
If Alice is losing, then she has half chance of zeroing out. In the other half, Alice wins, and thus the probability of her to win becomes P(2a). Similarly, if Alice is winning, then she has half chance of coming to the grand win, while another half chance drops her chance to P(2a - c). Thus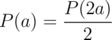 if
if 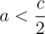 , and
, and 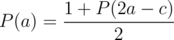 if
if 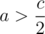 . We can simplify this into
. We can simplify this into 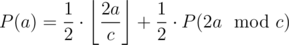 .
.
Yes, expand that.
Since this cycles, eventually we will arrive at computing P(a). We have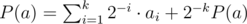 , where
, where 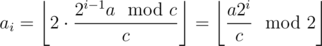 . (To prove the equality, divide cases: ai = 0 when the inside of the floor is smaller than 1, which gives blah blah blah.) In other words, expressed in binary, ai is the unit digit of
. (To prove the equality, divide cases: ai = 0 when the inside of the floor is smaller than 1, which gives blah blah blah.) In other words, expressed in binary, ai is the unit digit of 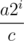 (which is a fraction, and thus unit digit means the digit exactly to the left of the binary point.
(which is a fraction, and thus unit digit means the digit exactly to the left of the binary point.
But hey, that multiplier 2i is actually useless. We can as well say ai is the i-th digit behind the binary point of ; multiplying by 2i simply slides the binary point around.
; multiplying by 2i simply slides the binary point around.
What does this mean? This means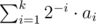 is actually simply constructing the binary expression of
is actually simply constructing the binary expression of  to k digits behind the binary point (with a zero integer part). So let's call this part
to k digits behind the binary point (with a zero integer part). So let's call this part 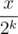 for some x (namely the period of
for some x (namely the period of  ). Also note that
). Also note that 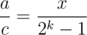 , since it is the sum of
, since it is the sum of 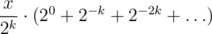 ; we repeat the number x every k digits behind the binary point.
; we repeat the number x every k digits behind the binary point.
And since we can move the term 2 - kP(a) to the front, we now have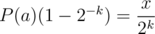 , or multiplying with
, or multiplying with 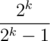 , we have
, we have 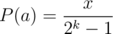 .
.
Wait. Since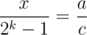 , this means
, this means 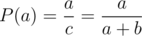 .
.
Problem solved.
Of course, this is only for a, b of different parities. But we can use a similar induction on the largest power of 2 that divides a + b, just in the first part of this solution, to conclude similarly: the probability of Alice winning if her balance is a versus Bob's b is simply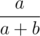 .
.
This might have various rigor issues.
LOL
In every state (except the special case of a and b equal), there is a 50% chance that the game will end, and a 50% chance that we will move to a new state. So we simply run the simulation for many steps, and with each step the likelihood of the current state (i.e. its influence on the final result) gets cut in half. 1000 iterations should be more than enough to get a result within 10^-5 of the correct answer.