Hi everyone, I'm trying to solve 316E3 - Summer Homework. Despite reading the tutorial link, I could't understand clearly the solution. Could you explain me more detail??
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | djm03178 | 152 |
| 7 | adamant | 152 |
| 9 | luogu_official | 151 |
| 10 | awoo | 147 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/23/2025 14:52:23 (k2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











The key is the merging step
While merging and
and  , we need to shift the Fibonacci multiplier of the second one by (l2 - r1) to the right , so that we get
, we need to shift the Fibonacci multiplier of the second one by (l2 - r1) to the right , so that we get 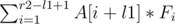
Shifting can be done by using identity Fn + m = FnFm - 1 + Fn + 1Fm
F[n+m+1] = F[n]*F[m-1] + F[n+1]*F[m] ??
Yes. Proof can be found from matrix exponentiation, or by induction here
Then make 2 segtree, for maintain (supposed to be
(supposed to be 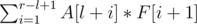 (supposed to be
(supposed to be
seg1) andseg2).Sorry if this explanation seems unclear. More detail you can check my submission 7338693
wow, I've got it. Thanks you very much :)