Hello everyone,
I'm struggling for a quite long time with certain problem (like 4 real attempts to solve it). Here is problem statement:
You are given a city which is represented by graph which is a tree (of course road intersections are nodes and roads are edges). Your task is to light every road in the city, you can do this by building street lights on road intersections. When there is street light on road intersection every road which comes out of it is lighted. Now your task is to find the minimum amount of street lights to light entire city and find amount of ways you can do this.
Input:
First line of input is n (n <= 100.000) — the number of road intersections in city. The next n-1 lines contain two integers a,b which mean that there is bidirectional road between intersections numbered a and b.
Output
First integer of output is optimal amount of street lights, and the second integer is the amount of optimal placements of streets lights in the city modulo 10007.
Examples:
Input:
4
1 2
2 3
3 4
Output: 2 3
Input:
5
1 2
2 3
3 4
4 5
Output:
2 1
Input:
6
1 2
2 3
1 4
4 5
1 6
Output:
3 5
Finding optimal number of street lights is quite simple, just two-color the tree and take the less often color. However finding amount of optimal street light placements is really hard for me. I was trying to root the tree at some node, and then find recurrence relation between node and its children so i can use dynamic programming. I believe in order to solve this problem one has to use at least two functions, h(v) — which is answer to the problem when there is street light in node v (where v is root of subtree), and l(v) when there is no street light at node (v), i tried to use some other functions like opt(v) — which represents optimal amount of street lights at subtree rooted at node v, but i just couldn't come up with recurrence relation.
Does anyone have any idea on how to solve this problem ?











for the second input (1 - 2 - 3 - 4 - 5), i think the answer should be 2, 1 instead of 1, 1.
You're right, i corrected it.
Your idea (functions h(v) and l(v)) is correct, you just need to add 2 more describing the number of optimal solutions for number of street lights in the subtree equal to h(v) and for l(v). You can calculate their values in parallel with calculating h(v) and l(v) — think how.
I can't really understand the definition of your functions, to me it looks like you just defined h and l again.
On second reading, it seems you defined them wrongly or just in a way that's hard to understand.
You can pick an arbitrary vertex as root of this tree, and then do DP on subtrees. In particular, for lighting all paths in a subtree rooted at v, you need h[v]: the optimal number of lights if there's a light in v, and l[v]: the same if there's no light in v. The DP involved is:
for l[v], all sons of v must have lights in them, so it's the sum of h[son(v)]
for h[v], all sons can, but don't have to, have lights in them, so it's the sum of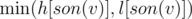
By recursively computing these functions by DFS, you can find the first part of the answer. The second part just needs p[v], denoting the number of ways to light the optimal number of lights in subtree rooted at v if there's a light in v (so for conditions of h[v]), and r[v], which is the same for l[v]. To compute them, you just need to work with the same DP as for the first part of the answer:
for r[v], you don't have a choice — a subtree of son s of v can only be lit in p[s] ways (because definition); these subtrees don't affect each other, so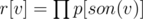
for p[v], may (or may not) have a choice for each subtree — again, for son s of v, it's p[s] + r[s] ways if h[s] = l[s], p[s] if h[s] < l[s], and you can figure out the 3rd case yourself; p[v] is again a product of these values for subtrees of all sons
You can calculate p[v] and r[v] right after h[v] and l[v]. The final answer is chosen similarly as those for subtrees in p[v]: if h[root] = l[root], it's p[root] + r[root] etc.
Thank you very much for deep explanation. Well i was pretty close to solving this (my idea with opt function), now i got AC with my code. Btw. there are some mistakes in your comment. When there is h[s] < l[s] then we multiply it by r[s]. And for starting conditions (when we get to leaf) this is:
h[leaf] = 1 l[leaf] = 0 p[leaf] = 1 l[leaf] = 1
Well i honestly don't know why p[leaf] = 1, intuitionally this should be p[leaf] = 0 (since there are no optimal light placements when there is light on the leaf), but this probably has something to do with the definition of function. Either way, thank you!
Can you please specify the link of the problem. I want to test my code. Thank you.
I didn't really look into this blog for long time, and i hope you can still read it. Here is the link:
http://pl.spoj.com/problems/LCITY/
Thanks for the link :)
But the problem is now hidden due to some reasons :/