In each second, we will blend $$$\min(x, c)$$$ fruits. So time taken is $$$\displaystyle \left \lceil \frac{n}{\min(x, c)} \right \rceil$$$
Submission — 282005858
$$$n$$$ is the winner. $$$n-1$$$ will lose only against $$$n$$$.
For others, if we make them first against $$$n-1$$$ and atlast we have $$$n-1$$$ and $$$n$$$ fight, their score will be added.
So the final answer will be $$$A_1+A_2+....+A_{n-2}+A_{n}-A{n-2}$$$
Submission — 282011553
Let's say we know some string $$$s$$$ is a substring of $$$t$$$.
How can we extend it to find char just after this?
The idea is to query for $$$s0$$$ and $$$s1$$$; if one of them returns true, add that char to s and continue again.
If both $$$s0$$$ and $$$s1$$$ return false, then we know that our current string is the suffix of $$$t$$$. Now query for $$$0s$$$ and $$$1s$$$. and keep adding it in front.
In the worst case, this make take $$$2n+2$$$ queries. To avoid this, if $$$0s$$$ returns true, add $$$0$$$ in front. Otherwise, we know $$$1s$$$ will return true, so directly add it without asking.
Submission — 282024928
2013D - Minimize the Difference
What is the minimum possible value of the whole array?
One of the value must be less than or equal to the average of the array.
Now, notice that we only do -ve operations on the first element.
What is the minimum possible value of a2....,an?
(Again, think an average of a2....,an)
Similarly for every i, we will reduce (a1,a2,....ai-1) can only increase values in (ai,ai+1,.....,an).
So, what is the minimum value in this part?
(Again think average of ai,....,an)
Now, if we take the minimum of all of the above values, we know for sure that the final minimum is less than or equal to the above value.
As it turns out always possible to create an array such that above value will be the minimum possible.
Do similar stuff for maximum value and print their difference.
Submission — 282029106
What is the minimum value we can have first value? Take minimum.
Now, for the second element, find the element such that gcd(p1,ai) is the minimum possible.
In general, it greedily finds the next value such that gcd reduces as much as it can.
Submission — 282034547
2013F1 - Game in Tree (Easy Version)
Let's pick this graph, and say we want to find the answer when Bob starts at node 8. 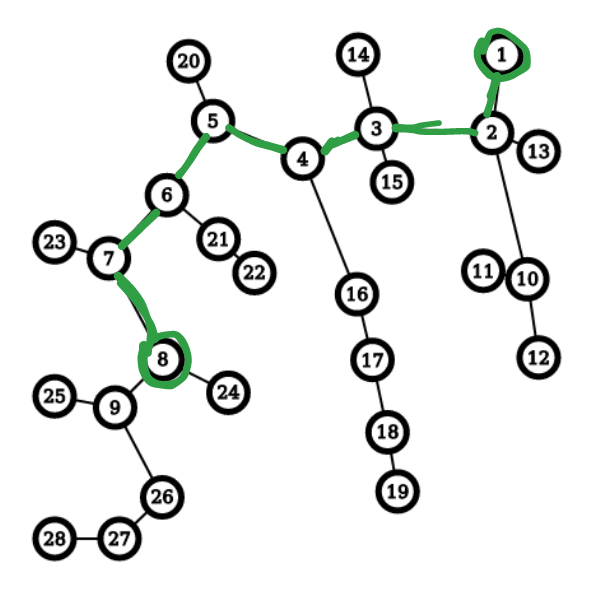
The game will proceed as follows: both Alice and Bob will move towards each other on the path between 1 and 8.
At some point, one of them will leave this path, allowing another person to take all remaining nodes if they want.
We don't really need a complete tree, just the distances of how long someone can go if they leave this path. The depth array ($$$d_1,d_2,...,d_k$$$) becomes $$$[0,2,1,4,1,2,1,4]$$$
Now, if Alice leaves at node 2, then they will travel a total of 4 nodes. We can
Now, if Alice leaves at node 2, then they will travel a total of 4 nodes.
Formally, if Alice leaves at ith node on this path, the distance she will travel is $$$i+d_i$$$ These will be distances for the example above. $$$[1,4,4,8,6,8,8,12]$$$
If Bob leaves at ith node on this path, the distance he will travel is $$$k-i+1+d_i$$$ These will be distances for the example above. $$$[8,9,7,9,5,5,3,5]$$$
Now, we can brute force game theory problem. FindWinner(aliceIdx,bobIdx,Turn) denotes who will be the winner if Alice is at aliceIdx on path, Bob is at bobIdx on path, and turn is (Alice/Bob) based on who is going to play.
At each turn player can see who will be the winner if they leave the path, and if they do not, and make a rational decision based on it.
Roughly, the following is the pseudo code -
// returns true if Alice wins, and false if Bob wins.
bool FindWinner(const lli aidx,const lli bidx,const bool isAliceTurn){
if(isAliceTurn){
// if Alice continues on the path.
if(aidx+1<bidx&&FindWinner(aidx+1,bidx,!isAliceTurn))
return true;
// if Alice leave at current node.
// You can use segment tree for this range max query.
if(aliceDist[aidx]>max(bobDist[aidx+1:bidx]))
return true;
return false;
}
// if Bob continues on the path
if(aidx+1<bidx&&!FindWinner(aidx,bidx-1,!isAliceTurn))
return false;
// if Bob leave at current index.
// You can use segment tree for this range max query.
if(bobDist[aidx]>=max(aliceDist[aidx:bidx-1]))
return false;
return true;
});
Submission — 282075612










Nobody that I've talked to so far was able to prove the solution for D. Anyone with a proof? I'm eagerly waiting for the editorial because I'm also not able to prove it...
ignoring the very long paragraph above we are trying to prove that in the optimal answer the min will be the maximum possible min we can achieve , right ?
Yes, you want to prove that achieving maximum min and minimum max at the same time is possible.
hey, you got anything?
i am still looking for a proof