Can anyone Guide me how to optimize this relation 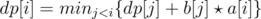 where b[j]>=b[j+1] and a[i]<=a[i+1] .I know for optimization use convex hull trick and i read convex hull trick ,but i don't know how to use this trick to optimize this Dp relation.
where b[j]>=b[j+1] and a[i]<=a[i+1] .I know for optimization use convex hull trick and i read convex hull trick ,but i don't know how to use this trick to optimize this Dp relation.
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | adamant | 152 |
| 6 | djm03178 | 152 |
| 8 | Qingyu | 151 |
| 9 | luogu_official | 149 |
| 10 | awoo | 147 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/20/2025 22:10:39 (i1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Well initially start with an empty set of lines, then after you calculate dp(i) add the line Ax+B witb A=b(i) and B=dp(i). Then if at some point you want to calculate dp(i) then you just run a query with x=a(i). The b(j)<=b(j+1) allows adding lines without using a dynamic set and a(i)<=a(i+1) allows solving the problem using pointer walk on the set of lines instead of doing binary each time, thus reducing the running time to amortized O(1) per query.
Sorry for using () instead of [] im writing from a phone.