Недавно AlexanderBolshakov показал в этом посте — который без сомнения скоро канет в небытие потому что его заминусовали — несколько интересных задач со старинной олимпиады. С Zlobober стали они обсуждать задачу T4:
3млн человек с разными фамилиями выстроились в одну колонну и записали каждый у себя на бумажке фамилию свою и стоящего впереди (кроме первого). Бумажки у них отобрали, перемешали и в произвольном порядке в виде пар фамилий записали на магнитную ленту (односвязный список).
Как возможно быстрее узнать фамилию человека на 1234567 месте? Ограничение по памяти — не более 32 магнитных лент (списков) и не более 64кб памяти с произвольным доступом.
А правда, как это решать?
Мне на ум приходит пока следующее:
Ну сначала препроцессим данные — отсортируем и заменим фамилии на порядковые номера по алфавиту например, после чего исходную ленту перезапишем в виде пары чисел. Это у нас займёт O(N*logN).
Дальше из исходной ленты мы создадим две копии и отсортируем каждую — одну по порядку возрастания собственных фамилий, другую по порядку возрастания предшествующих.
Допустим если фамилии были однобуквенные и люди стояли так:
A D R O C I T E
То после этого шага (который тоже займёт O(N*logN)) у нас будет две ленты:
AD CI DR IT OC RO TE OC AD TE CI RO DR IT
Эти пары можно явно слить за один проход в тройки (отбрасывая AD и TE как концевые по тому признаку что для них нет пары):
OCI ADR CIT ROC DRO ITE
Эти тройки я опять могу скопировать и отсортировать по первым и последним буквам, потом слить и получить пятёрки, дальше фрагменты по 9, 17 и т.п. Собственно хранить эти фрагменты целиком необязательно, от каждого нужна первая и последняя буквы.
От каждого шага будем оставлять по одной отсортированной (по первым буквам) ленте — с двойками, тройками, пятёрками, девятками... Так у нас будут ленты с фрагментами длиной до 2^20 и их формирование займёт O(N*logN^2) по-моему.
В принципе после этого я могу любую фамилию на этих лентах отыскать также за O(N*logN).
Но мне сдаётся что у меня получается много лишних действий (хранение ненужных фрагментов в том числе) избавившись от которых можно было бы формирование лент ужать до O(N*logN). Кроме того Я ни на одном шаге не попытался использовать память с произвольным доступом.
Правильны ли мои размышления и что тут можно улучшить?
В то же время я подозреваю что лучше чем O(N*logN) сделать в принципе нельзя, но в зависимости от ухищрений константа может быть очень разная.
Мысли такие... Есть массив из фамилий и из наборов фамилия-фамилия, у каждой фамилии (человека) есть индекс. Заведем два массива start и end, куда запишем для каждого человека номер из массива записок, где он стоит первый, и где — второй (есть гарантия, что в каждом элемента массива только одно значение). Заполнить эти массивы можно за один проход списка фамилия-фамилия.
Теперь создаем пустой список. Берем случайного человека, ищем записку, где он первый, из start[index]. Записываем в конец списка его фамилию и фамилию следующего человека. Теперь ищем записку, где первым стоит сосед этого начального человека, делаем то же самое, пока не встретим человека, который нигде в записках не стоит первым.
Получаем список из людей, где первый человек — тот случайный. Аналогично заполняем начало списка, ищем строку где тот человек последний и так далее. Первый человек в списке — тот, который в записках нигде не стоит последний.
Итого — обращаемся к списку по индексу [123456789]. Сортировки и прочих сложных вещей нет... Но и в 64кб не укладывается
Понимаете, если бы в задаче не было ограничения на размер ОЗУ, то задача была бы совсем тривиальной.
Только если они полностью влезут в память. Если же мы вынуждены хранить их на магнитной ленте, то для этого потребуется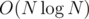
времени. Я потом попытаюсь доказать, что за лучшее время это сделать невозможно.
Это Вы описали самый тупой алгоритм топологической сортировки, работающий за O(N2). Кстати, при его реализации тот факт, что у нас всего 64КБ памяти, нам совсем не мешает — можно держать в памяти только один элемент списка, а остальные записывать на ленту.
Извините, где тут топологическая сортировка за n^2? Разве я не указал, что для поиска таблицы, где человек с номером index первый или второй, используются массивы start[index] и end[index] с УКАЗАНИЕМ на номер таблицы фамилия-фамилия, а не перебор всех таблиц, которых 2999999. Иначе для чего, по-вашему, эти массивы? Не вижу ничего, что тут n^2, только n везде :/ Спасибо, я не вчера начал программировать и соображаю, что такое перебирать три миллиона записей каждый раз. Перечитайте еще раз
Перечитал. Я и правда туплю. Прошу прощения.
Но в этой теме все равно нет смысла писать о том, как решать задачу при наличии достаточного количества ОЗУ. Скажем так, тема совсем не "новичковая", а "не новички" это и так знают.
Я смог найти решение, работающее за
при условии наличия 
магнитофонов.
Я анализировал задачу "имея записанный на ленту массив A размера N и перестановку P чисел от 1 до N, записать на ленту массив B, полученный из массива A применением к нему перестановки P". У меня получилось строго доказать нижнюю границу
, где M — количество магнитофонов.
Идея доказательства: существует всего N! перестановок и, соответственно, Ω(N!) различных возможных состояний наших магнитофонов. У нас существует O(M2) различных операций с магнитофонами (вида "сдвинуть головку" и "скопировать что-то из текущего положения головки магнитофона A в текущее положение головки магнитофона B"). Итого за K операций мы можем получить O((M2)K) различных состояний, итого чтобы получить N! различных состояний, нам нужно сделать
операций.
Давайте теперь придумаем алгоритм выполнения такой перестановки. На самом деле, он будет полностью идентичен квиксорту с разбиением на O(M) интервалов и рекурсивным вызовом от каждого интервала. Думаю, рассказывать, как это реализовать, не обязательно.
Ну что же, спасибо авторам задачи, я благодаря им узнал много нового.
http://logic.pdmi.ras.ru/csclub/courses/hugedataalgorithms — вот курс об алгоритмах во внешней памяти.
Первая лекция, задача ранжирования списка.