I am trying to solve the following problem but I am getting 'java.lang.OutOfMemoryError'
Problem statement:
Suppose we have a plane with dots (with non-negative coordinates). We make three queries:
1)add dot at (x , y)
2)count number of dots in rectangle (0 , 0), (x , y) — where (0 , 0) if down-left corner, (x , y) is up-right corner and sides are parallel to x-axis and y-axis.
total no.of queries is M and the constraint are as follow
0<x,y<=10^9;
0<M<=100000(=10^5);
the solution given in this topcoder tutorial uses tree[max_x][max_y] which is tree[10^9][10^9] and surely one will get 'out of memory' error.
I have tried to compress the value of x,y (mapping {1,2,3..} to input set) but still it takes 10^5*10^5 which is out of bound.
Plz tell me what is the right way to solve this kind of problem.











EDIT: O(n log^2 n) memory. Fenwick tree on map. (Zlobober pointed it out)
First, input all (x, y). Use map, set or binary search to compress numbers.
For example: (1, 10^9), (10^9, 1), (2, 2), it will become: (1, 3), (3, 1), (2, 2)
(x: 1, 10^9, 2 -> 1, 3, 2
y: 10^9, 1, 2 -> 3, 1, 2).
Comment if you think my post unclear. EDIT:
Sorry for not read the post carefully.
one of interesting/similar problems: http://stackoverflow.com/questions/15219782/counting-total-number-of-points-inside-2-circles
It is clear but I have to define Array[3][3] (in your example) if i use the fenwick tree (method shown in topcoder tutorial)
if I have 10^5 point then Array[10^5][10^5] will be out of bound.
I think i am missing something that might be obvious.(I know only one method shown in link) Plz guide me
I would be very thankful to you.
You can use hashmaps and create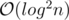 elements, so total time and memory usage is
elements, so total time and memory usage is 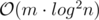 .
.
Array[x][y]only when requested. Each query creates not moreCould you please give any example to make it more clear.. Thanks
Warning: beware of probable bugs.
Something like this:
Example of Tests:
Output (seems to be correct):
A simple 2D Fenwick tree can solve this problem.
Sure, OP already knew that; He just ask to optimize his program's memory.
It's not a Fenwick tree problem, it's a 2D segment tree problem. 'nuff said.
You're wrong. 2D Fenwick tree can be implemented using O(NlogN) memory in the same manner as 2D segment tree.
First you compress all coordinates and create array A[], where element A[x] is responsible for a vertical strip containing all points with x-coordinate between F(x) and x (F(x) is the function you prefer to use in Fenwick tree, for me it is
x - (x & (x - 1)).Each element A[x] will be a Fenwick tree itself, responsible for its vertical strip. But it will have size equal to the number of elements in that vertical strip that is generally smaller than 105. You should also compress y-coordinates only for this segment. So, A[x] is a Fenwick tree along the vertical direction.
It's easy to see that this structure contains elements, can be built in
elements, can be built in  time and can answer queries of form "number of points in rectangle" in
time and can answer queries of form "number of points in rectangle" in 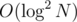 time. It's the fastest solution for this problem that I know. It's much faster than 2D segment tree.
time. It's the fastest solution for this problem that I know. It's much faster than 2D segment tree.
Obviously it's also much faster than implementing 2D-Fenwick on Map/UnorderedMap.
Thanks a lot.
So far I was storing every point in fenwick regardless of its value but I got that we don't actually need to store the point whose value is zero.
Oh, I didn't realize it could be solved that way. I suppose the "compress y-coordinates only for this segment" includes maps with some elements total, so it doesn't have the awesome constant of BIT (and doesn't work online), but it should be pretty fast.
elements total, so it doesn't have the awesome constant of BIT (and doesn't work online), but it should be pretty fast.
It has even more awesome constant then BIT =)
You don't need to use maps for compressing y-coordinates. Lets' store for each x also a vector with y-coordinates of this segment in increasing order. We can use this vector for comressing y-coordinates.
Pseudocode of such structure:
What do you mean by "it doesn't work online"? Usual 2D segment tree doesn't work completely online also.
Online as in IOI 2013 Game. (if it had summation instead of GCD)
I am not able to understand how it works? can anyone please explain this code? also what does
A[x].push_back(0);in your code does. thanks!The vector is initially empty so we need to fill them with 0.
hey can u explain F[x][y] term in your code. Thanks
How will it take O(NlogN) memory? If N = 10^5, then even after coordinate compression there would be N values of x and y both.
First of all, this thread is years old, so it is often frowned upon to "necropost" and bring it back to life.
However, what Zlobober is saying is to compress the values within each position of the first layer tree. If we talk about tree[x][y], x is the position of the first layer. If we set an array of this size, you are correct — it will be too much memory. However, the amount of distinct 'y' values differs for different positions 'x'. We only need to assign memory to the order of how many items that will ever appear at 'x'.
Now, suppose we have an item we want to insert into our structure. Its 'y' value will go into at most logN 'x' values clearly, and each time it goes into something it uses 1 piece of memory. So each for N insertions we use NlogN memory. We can use vectors to pre-process which 'y' values show up at a certain 'x' value. Therefore, we avoid creating the whole 2D array.
I hope this is clear.
Maybe someone could help me with Fenwick tree problem too?
If we use simple Fenwick tree for finding sum, and every element of initial array is 0 or 1, and we have 2 type of queries:
1) replace given "1" to "0" value (and only 1->0 replacements, so, count of "1" decreases every time)
2) find position of K-th "1" in the array
So, "1)" could be done in O(log2(N)), and what about "2)"? How to make second query in O(log2(N)) time too, not in O(log2(N)^2) ?
No any ideas?