http://apps.topcoder.com/wiki/display/tc/SRM+527
For P8XGraphBuilder, I am not able to understand the proof of the "evil theorem" by dolphinigle
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | djm03178 | 153 |
| 7 | adamant | 152 |
| 8 | luogu_official | 149 |
| 9 | awoo | 147 |
| 10 | TheScrasse | 146 |
http://apps.topcoder.com/wiki/display/tc/SRM+527
For P8XGraphBuilder, I am not able to understand the proof of the "evil theorem" by dolphinigle
| Name |
|---|



Let's restate the evil theorem:
If we have an integer N ≥ 2, along with N more integers d1, d2, ..., dN where 1 ≤ di for all i and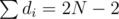 , then there exists a tree T with labeled vertices v1, v2, ..., vN such that vertex vi has degree di.
, then there exists a tree T with labeled vertices v1, v2, ..., vN such that vertex vi has degree di.
The proof is by induction.
When N = 2, we have 1 ≤ di ≤ N - 1 = 1 for all i, and hence the only possible tuple of di's is (1, 1). Clearly there exists such tree T: simply draw a single edge connecting two vertices v1, v2. The degree of both v1 and v2 is 1, so we have proved the base case.
Now suppose that for some N = K, K ≥ 2, the statement is true. We will prove that the statement is also true for N = K + 1.
Observe that there is some di that is equal to 1. If not, then we need to have 2 ≤ di for all i, but then their sum is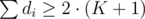 since there are K + 1 numbers, each of which is at least 2, while on the other hand we know that
since there are K + 1 numbers, each of which is at least 2, while on the other hand we know that 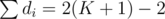 , contradiction. Without loss of generality, suppose dK + 1 = 1, otherwise just relabel everything.
, contradiction. Without loss of generality, suppose dK + 1 = 1, otherwise just relabel everything.
Also, similarly, there must be some di that is not equal to 1. If not, then all of them are equal to 1, and thus their sum is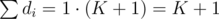 , while on the other hand we know that
, while on the other hand we know that 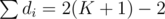 . These two can only be equal when K = 1, but we assumed K ≥ 2, so this is wrong. Still without loss of generality, suppose d1 > 1.
. These two can only be equal when K = 1, but we assumed K ≥ 2, so this is wrong. Still without loss of generality, suppose d1 > 1.
Now we draw an edge between v1 and vK + 1. This satisfies the degree requirement for vK + 1, so we may remove it and dK + 1, and reduce d1 by 1 into d1' = d1 - 1, since v1 has connected with one vertex and so only needs d1 - 1 more. Now observe that we are left with K integers, all of them are positive (d1' is still positive since d1 > 1 and so d1 - 1 > 0), and their sum is 2K - 2 (since we subtracted dK + 1 = 1 from the sum, as well as 1 from d1 becoming d1', thus subtracting 2 from 2(K + 1) - 2 giving 2K - 2). Thus by our induction hypothesis, there exists a tree connecting v1, v2, ..., vK. Adding back the edge between v1 and vK + 1 completes the construction of our desired tree, and thus the claim holds for N = K + 1.
Since we have proved the base case and the inductive case, by mathematical induction we're done; the evil theorem is true.
So the evil theorem also says that 1 ≤ di ≤ N - 1, not only 1 ≤ di. But this is immediate: if any of the di exceeds N - 1, then the remaining sum will be less than (2N - 2) - (N - 1) = N - 1, and thus we have N - 1 numbers adding to less than N - 1. Clearly some number is going to be lower than 1, contradiction. Thus the upper bound is automatically fulfilled.
Thanks for the excellent explanation! I get it now :)